A continuous time model for a short-term multiproduct batch process scheduling

Modelo de programación de la producción por lotes de múltiples productos con tiempo continuo

In the chemical industry, it is common to find production systems characterized by having a single stage or a previously identified bottleneck stage, with multiple non-identical parallel stations and with setup costs that depend on the production sequence. This paper proposes a mixed integer production-scheduling model that identifies lot size and product sequence that maximize profit. It considers multiple typical industry conditions, such as penalties for noncompliance or out of service periods of the productive units (or stations) for preventive maintenance activities. The model was validated with real data from an oil chemical company.  Aiming to analyze its performance, we applied the model to 155 instances of production, which were obtained using Monte Carlo technique on the historical production data of the same company.  We obtained an average 12 % reduction in the total cost of production and a 19 % increase in the estimated profit.

En la industria química es común encontrar sistemas de producción caracterizados por tener una sola etapa o una etapa cuello de botella,  con múltiples estaciones paralelas, no idénticas, y con costos de preparación o alistamiento dependientes de la secuencia de producción.  Este artículo propone un modelo lineal mixto de programación de la producción que busca identificar el tamaño de lote y la secuenciación de productos con el objetivo de maximizar el beneficio. Considera múltiples condiciones típicas de la industria, tales como la penalización por incumplimientos, la programación de mantenimientos preventivos de las estaciones y la disponibilidad temporal de las estaciones. El modelo se validó con datos reales de una empresa de la industria del petróleo. Buscando analizar el desempeño del modelo, se analizaron los resultados de aplicar el modelo a 155 instancias generadas aplicando simulación Montecarlo, a los datos históricos de producción de la misma compañía.  Se obtuvo una reducción del 12 % en la reducción total del costo de producción y un incremento del 19 % en la utilidad estimada. 

Jenny Díaz-Ramírez ¹, and José Ignacio Huertas ²

---

¹ Ph.D. Industrial Engineering, Full Professor, Departamento de Ingeniería, Universidad de Monterrey, Monterrey, Mexico. E-mail: jenny.diaz@udem.edu.

² Ph.D. Mechanical Engineering. Full Professor, Departamento de Ingeniería Mecánica, Tecnológico de Monterrey, Monterrey, Mexico. E-mail: jhuertas@itesm.mx.

---

How to cite: Díaz-Ramírez, J., and Huertas, J. I. (2018). A continuous time model for a short-term multiproduct batch process scheduling. Ingeniería e Investigación, 38(1), 96-104.

DOI: 10.15446/ing.investig.v38n1.66425

---

ABSTRACT

---

Keywords: MIP modeling, goal programming, batch process scheduling, short-term scheduling, mathematical formulation, Monte Carlo simulation.

---

RESUMEN

---

Palabras clave: programación entera mixta, programación de la producción por lotes, industria química, modelación matemática, simulación Monte Carlo.

---

Received: July 20th 2017

Accepted: October 25th 2017

---

Introduction

The chemical industry is characterized by having repetitive production operations in which chemical reactions occur either in batches or in continuous flow of liquid or gaseous material, rather than in discrete units. This aspect, together with the limitations of several processes, makes the planning of the production process, of a greater complexity than those of the manufacturing industry.

Figure 1 presents an outline of the process. A basic feature of this production process is that it involves multiple stages but there is a main bottleneck stage that uses the most expensive operating resources of the plant. Those resources are the chemical reactors, hereinafter referred to as processing units or just units. This fact forces the other stages of the process to subordinate to these units, and allows the simplification of the scheduling process to the single bottleneck stage as in (Marchetti & Cerdá, 2009). It also requires the most efficient use of these units by using them at their maximum load and by minimizing setup times. Setup times are often associated with cleaning operations, tool changes and machine shapes. Non-identical units imply different capacities and different processing times for a given product. It also implies that there is a subset of units that can process a particular product. The planning problem also includes the scheduling of maintenance operations.

Figure 1. Illustration of the chemical flow process.

Source: Authors

The production planning process usually includes a stage prior to the planning horizon, in which the various orders of a product are grouped and, after checking the inventory status, a “total production demand” is determined for each product. Products may have intermediate due dates, i.e. some partial or total demand for a particular product may have more than one specific due date within the planning horizon for either the same or different customers. A model should then consider an objective function with penalization by violations in demand goals and other policies, and subject to operations constraints (i.e. sequence, product-unit compatibility and sequence dependent preparation times).

Although important research efforts have been made in this area (Harjunkoski, et al., 2014; Mendez, Cerdá, Grossmann, Harjunkoski, & Fahl , 2006), some challenges have been identified related to the ability of academic proposals to represent a) the actual features of industrial problems (Novara, Novas, & Henning, 2016), and b) the size of problems that can realistically be solved with these methods.

This article addresses the first challenge by solving a short-term batch scheduling for a chemical company context. The operational issues considered in this work have not all been addressed before: (a) the product compatibility expressed by sequence dependent preparation times, which is given by the number of washing procedures of the unit required between two consecutive products, and by sequence dependent costs; that is, costs that depend on the number of washing operations; (b) The flexibility of partially or totally rejecting the processing of a specific product over a given horizon is also handled considering the demands; (c) Non identical parallel units; (d) inventory reorder points, and inventory (minimum and maximum) limits of each product; (d) Overproduction, which is a major problem due to storage limitations, is controlled with upper bounds; (e) Product priorities are also considered based on marketing conditions; (f) The option of having multiple batches per order; and (g) A monolithic approach, in the sense that not only consists on the definition of the number and size of batches of the same product but of the same order, and their sequence. This approach has shown to yield better solutions than those obtained by two-stage methods (Castro & Novais, 2009).

Moreover, the computational complexity of these types of problems (i.e. NP hard) has proved to be very sensitive to several parameters and their inter-dependencies (Koçlar, 2005; Transchel, Minner, Kallrath, Löhndorf, & Eberhard, 2011). Despite this, the performance of several of the approaches has been evaluated numerically well with few examples, sometimes small, or with real data given by very specific conditions (Harjunkoski, et al., 2014; Novara, Novas, & Henning, 2016). Thus, to address the second challenge, the robustness of this proposal was validated using a set of data generated using the Monte Carlo technique from real data, which is an uncommon approach for testing these type of models.

Literature review

Optimum planning of batch production has received great attention in recent years because of its positive impact on production efficiency and economic benefit (Xue & Sun, 2010). The latest revisions of batch scheduling problems can be found in Allahverdi, Ng, Cheng, & Kovalyov (2008), Harjunkoski, et al. (2014); Jans & Degraeve (2008), Karimi, Ghomi, & Wilson (2003), Mendez, Cerdá, Grossmann, Harjunkoski, & Fahl (2006) and in Zeballos, Novas, & Henning (2011). The last four focused on industrial models. Scheduling problems considering maintenance can be found in (Chang & Manikas, 2009; Tsai & Wang, 2017). An extensive part of the literature deals with the problem of the size and the programming of batches with discrete time intervals (Harjunkoski, et al., 2014; Merchan, Lee, & Maravelias, 2016; Velez, Dong, & Maravelias, 2017). Though this is perhaps the most general approach (Harjunkoski, et al., 2014), its major drawback is related to data accuracy, and as Jans and Degraeve (2008) say: “The main limitation of this approach is the unnecessary increase in the overall problem size due to the introduction of additional binary variables associated with each discrete time interval”. These drawbacks have attracted the development of continuous time scale models.

Additionally, multi-product and multi-stage continuous programming time MILP models have been proposed. They consider sequence-dependent preparation times, unit-dependent preparation times and due dates (Afzalirad & Rezaeian, 2016; Atan & Akturk, 2008; Castro & Novais, 2009; Karimi & Liu, 2005; Mendez, Henning, & Cerda, 2000; Xue & Sun, 2010). Novara, Novas, & Henning (2016) performed a review on scheduling problems of resource-constrained multiproduct multistage batch plants. They divided the methods in two groups: those that assume a single batch per order and after 2008, approaches that manage orders comprising multiple batches. Table 1 shows a summary of some continuous short-term multiproduct scheduling problems found in the literature. However, none of them is fully adaptable to the conditions previously discussed.

Among the latest proposals, Novara, Novas, & Henning (2016) and Afzalirad & Rezaeian (2016) address several features of industrial environments (e.g. forbidden product-equipment assignments, sequence-dependent changeover tasks, dissimilar parallel units at each stage, etc.). The first ones proposed a constraint programming model for multiproduct multi-stage batch scheduling problems. They handled multiple-batch orders by defining a campaign operating mode, which is common in practice but can produce suboptimal solutions, since a campaign mode consists of scheduling a predefined number (or range) of batches of the same product. Afzalirad & Rezaeian (2016) formulated a discrete model, proposed two meta-heuristic algorithms to solve it, and validated them with 14 randomly generated examples. Recently, Hinder & Mason (2017) exploited known order-based properties of optimal solutions for simpler single stage, family setup times and a single machine scheduling problem. In this case, large scale instances are generated and solved up to 1 080 jobs and 270 families.

Table 1. Some related continuous MILP literature for multiproduct short-term batch scheduling problems

Authors	Stage	Setup	PUnits	Objective(s) & Comments
(Hinder & Mason, 2017)	S	F-	-	Min lateness Branch & Bound and theory for tight bounds. 75 instances generated for each combination of # jobs and # families (up to 120, 10).
(Afzalirad & Rezaeian, 2016)	M	SD UD	Rm	Min makespan One example: 6 jobs, 2 units 14 randomly generated instances to evaluate 2 meta-heuristics (up to 6 jobs, 3 units)
(Novara, Novas, & Henning, 2016)	M	SD	Rm	Min makespan, total tardiness & # tardy batches. Campaign-based operation 5 examples – up to 22 orders
(Nekoiemehr & Moslehi, 2011)	S	SD	S	Max earliness, min tardiness Polynomial time algorithm. 1 Example: 5 jobs 3840 instances of 8-25 jobs
(Jin, Gupta, Song, & Wu, 2010)	S	SD	Rm	Min max lateness Real data and randomly generated data. Tabu search.
(Xue & Sun, 2010)	M	SD	Im	Max weighted completion times. Penalties for tardy orders. Validation with examples.
(Subbiah, Tometzki, Panek, & Engell, 2009)	M	SD	Rm	Min tardiness Intermediate due dates Time automated model Reachability analysis. 2 cases. Up to 29 orders, 6-8 operations
(Atan & Akturk, 2008)	S	I	S	Max profit. Tardiness for lateness. Order acceptance/rejection. Controllable processing times.
(He & Hui, 2008)	S	SD UD	Rm	Min makespan and total tardiness (multi-objective) Penalty for violating due dates 8 examples. Large scale: 50 orders.
(Osorio G., Castrillón M., Toro C., & Orejuela C, 2008)	S	SD	Im	Min makespan With interruptions Job shop recirculation Example: 13 operations
(Omar & Teo, 2006)	M	SD	Im	Min sum earliness/tardiness Hierarchical method. Validation with real data.
(Liu & Karimi, 2005)	M	I	Rm	Min makespan Validation with examples
(Hassin & Shani, 2005)	S	I	Im	Earliness /tardiness. Penalties for non-execution. Polynomial algorithms. Distinct due dates.
This work	S	SD UD	Rm	Max profit. Penalties for partial execution and tardiness. Priorities, maintenance and inventory levels considered. Multiple batches for intermediate due dates. Real data and randomly generated instances: 155: up to 28 products.

S: Single, M: multiple, SD: sequence dependent, UD: unit dependent, I: Independent, F: family, PUnits: Parallel units, Im: identical machines, Rm: unrelated machines, max: maximize, min: minimize.

Source: Authors

Problem description

The problem can be classified according to Mendez et al. (2006) as shown in Table 2, and according to Allahverdi et al. (2008), as an R | STsd,b | TSC, where R refers to unrelated machines, STsd,b refers to preparation times dependent on the batch sequence or family of products, and TSC refers to the performance focused on minimizing preparation or change time. Although in this case, it is measured with a composite objective function including delays, due dates, and inventory policies.

Table 2. Problem Classification

Process topology	Single stage, parallel units
Assignment of equipment	Fixed
Connectivity of the equipment	Complete
Inventory Storage Policy	Finite final storage
Material transfer	Instantaneous
Lot size	Variable
Batch processing time	Variable
Demand patterns	Due dates: single or multiple. Horizon: variable
Exchanges	Sequence-dependent
Resource constraints	None
Time Restrictions	Maintenance
Costs	Equipment, material, exchanges
Degree of certainty	Deterministic

Source: Authors

The conditions and assumptions considered in this problem are: (a) Demand, capacity, processing times, units suitable for each product, inventory limits (minimum and maximum), and due dates for the time horizon are known and fixed; (b) raw material, units and other resources are always available; (c) There are no interruptions, unplanned unit breakdowns or reprocessing; (d) the parallel units are not identical, work at full load and can process at most one batch at a time; (e) setup times and costs depend on the degree of compatibility between two consecutive products; (f) a product can be processed in more than one unit, but at most once in each unit during the time horizon; (g) an order can be split in multiple batches according to the intermediate due dates; (h) the time horizon for each unit is independent and is a subset of the general planning horizon; and since the units constitute a very restricted resource, even the time horizon could be violated (and thus penalized); (i) given the short-term horizon, the programming of the first product in each unit considers its compatibility with the last product programmed in that unit during the previous horizon; (j) preventive maintenance operations are translated into maintenance demands and then they are considered as products with their own times and preparation goals.

The main assumption considered is that the problem can be simplified to a single stage process, focusing on the bottleneck process scheduling, in which transfer times are not relevant, and neither storage transfer policies are.

The basic decisions to be taken are the sequence of products in each unit, the lot size, which is the number of consecutive batches of a product in the same unit, and the follow-up of the start (continuous) time of each lot. Other decision variables control violations of various operational considerations.

Mathematical model

The proposed model uses a continuous time representation with network flow equations (for products and units), where both the lot size and the schedule are defined simultaneously. An event occurs at a global time point, considering immediate precedence, with an objective function of maximizing profits with penalties related to non-fulfillment of demands, due dates, inventories, and costs. The model is based on the longest path problem, with many side constraints, through a multilevel network, in which each route represents the schedule of one unit. Each path has a specific starting node, but all paths terminate at the same sink node. A node at any level represents the processing event of a product, which keeps track of sequence information with a binary variable, batch size with an integer variable, and initial processing time with a continuous variable. Finally, sequence, demand constraints and time-related constraints are formulated. The tracking of the last product processed in a unit during the previous planning horizon allows taking it as input data for the following period, to determine the compatibility of the first product.

By default, the due date for each product is set at the end of the scheduling horizon. When a product has more than one due date (i.e. partial deliveries with distinct due dates), then that product is divided into R + 1 products –the original plus R pseudo-products– each with its specific due date and demand, which is called “partial demand”. Thus, the sum of the production of these R + 1 products is the total demand of the original product.

Sets

IP Set of products plus required maintenance procedures, source nodes for each unit and a single end node l IP ={1, ..., N}.

I Set of products with demand greater than the minimum threshold

IM IP subset that includes only maintenance procedures .

IQ Subset of IP products including products with demand and maintenance procedures .

IR Subset of pseudo-products with specific due dates . If a product has delivery dates prior to the planning horizon, the product is decomposed into pseudo-products each with its own demand and delivery date. The demand for pseudo-products is less than or equal to the demand for the product from which it is decomposed.

K Set of units

Decision variables

Yik Product i batch size scheduled in unit k.

tik Processing start time of product i in unit k

bdi Uncovered demand of product (to reach reorder point)

bpari Uncovered demand of pseudo-product

bmi Uncovered demand of product (to reach minimum inventory level)

sdi Production excess of product (i.e. with respect to the reorder point).

smxi Production excess of product (i.e. with respect to the maximum inventory level).

latei Tardiness of product (i.e. with respect to the due date)

zu Objective function value.

Parameters

di Production demand of product (to reach reorder point)

dmi Production demand of product (to reach minimum inventory level)

dmxi Production demand of product (to reach maximum inventory levels)

pi,k Processing time of product i in unit k.

wi,j Number of washing procedures required in a sequence i – j.

DDi due date for product

spri Sale price of product i

pri Product priority i.

QRij QRi,j = 1 if pseudo-product has the same due date as the product from which it was decomposed; QRi,j = 0 otherwise.

RRi,j RRi,j = 1 if due date of seudo- product is earlier than that of product . Both i, j are pseudo-products from the same product . RRi,j = 0 otherwise.

Mk Scheduling horizon for the unit k. 

Ck Capacity of unit k.

t0k Scheduling start time on unit k. 0 ≤ t0k < Mk

WTk Duration of washing procedure in unit k

ri,k Ri,j = 1 if product i can be processed in unit k, Ri,j = 0 otherwise.

vci,k Processing variable unit cost of product i in unit k.

fck Fixed processing cost per hour in unit k.

pd Unit penalty for non-compliance with demand

pm, pmx Penalty for violation of minimum and maximum limits of production

ppar Penalty for non-compliance with partial demand (i.e. pseudo-products demand)

pw Penalty or costs of washing procedures

plate Penalty for violation of due dates.

mtk Multiplicative factor of the planning horizon (to
obtain a very large number)

mks Maximum allowed violation of the programming horizon.

MIP Model

(1)

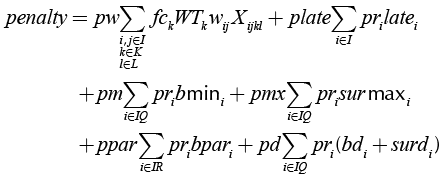(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

The objective function in Equation (1) is a profit maximization penalized by the violation of some of the operating restrictions. The first term on the right-hand side calculates the income generated by the total quantity produced minus the surplus with respect to the demand. The second term calculates the cost of production, including the costs of preparation, and finally, the third term is given by Equation (2). This equation penalizes (a) the inclusion of washing procedures, (b) late production, (c) production outside inventory limits, (d) partial deliveries not satisfied, and (e) differences from reorder points.

Equations (3) to (8) are related to sequencing. Equation (3) prevents overlapping and identifies the sequence. Balance equations are equations (4). Equations (5) and (6) compute the lot size Yik. Equations (9) and (10) restrict the initial and final nodes of each unit’s sequence.

Equations (9) to (13) deal with the demand. Equation (9) computes the amount of production scheduled and the differences from the demand to the reorder point. Equation (10) computes deviations from partial deliveries, and Equations (11) and (12) deviations from minimum and maximum inventory levels. Equation (13) limits the maintenance batch size to 1.

Related to time, Equation (14) computes violation on due dates, equations (15) and (16) ensure that the schedule of a given unit k begins at its own horizon time, and Equation (17) ensures the time ordering between pseudo-products. Finally, Equations (18) to (20) give the variables’ domain.

Numerical Experimentation

The proposed model was verified and validated with a set of instances generated from real historical information from a chemical company in Mexico. Figure 2 shows the experimentation process.

Figure 2. Experimentation process scheme.

Source: Authors

Through an interface in Excel®, the user feeds the model and calls the solver. Then, the output is translated again through the interface into an Excel output file. The model was coded in GAMS® software with the CPLEX® solver version 22.6 and run on a computer with 1.99 GB of RAM, with an Intel Xeon (R) CPU 5150 at a speed of 2.66 GHz, working under the windows operating system XP.

Pre-processing

The following trivial situations were identified so that variable levels were fixed before running the model, reducing the problem size:

a) All ;

b) if products i and j are incompatible;

c) if j is the first product in the sequence of k;

d) ;

e) if or .

Model validation

To validate the model, input parameters from a Mexican chemical company were used, corresponding to a typical production month, in which 30 products were produced, with 6 units enabled for production and no programmed partial deliveries. The horizon used was one month. Overall results are summarized in Table 3. Costs and profits are compared to the baseline (actual values of real case) in a scale of 100.

Table 3. Results of the model vs baseline

	Baseline	Model
Production total time (h)	2 695	2 645
Production total cost (base 100)	100	88
Total profit (base 100)	100	119
CPU time (sec)		22

Source: Authors

Random generated Instances

Goodness of fit tests were applied to historical 9-month data to describe product demand. In particular, the probability of a product being demanded in a month (i.e. the programming horizon used) and the mean and standard deviation of demand for each product were identified. Using the Monte Carlo technique, 155 instances were generated with a set of products no greater than 30, as shown in Table 4; some of them with a maximum of two partial deliveries (with distinct due dates) and with 4 units enabled.

Table 4. Generated instances description

Month	Instance	p	n	m	AvPn (ton)
1	1-20	28	2 650 - 3 360	1 796 - 2 262	2 596
2	21 – 40	28	3 707 - 4 369	2 416 - 2 873	2 584
3	41 – 60	14	2 453 - 2 903	1 698 - 2 014	1 453
4	61 – 80	17	2 308 - 2 776	1 579 - 1 907	2 384
5	80 – 95	14	2 167 - 2 237	1 370 - 1 604	1 694
6	96 – 110	23	2 053 - 2 123	1 290 - 1 532	1 602
7	111 - 125	28	1 940 - 2 010	1 188 - 1 449	1 811
8	126 - 140	17	2 651 - 2 723	1 636 - 1 893	2 750
9	141 - 155	19	1 804 - 1 876	1 146 - 1 373	1 701

p: number of products, n: number of variables, m: number of equations, AvPn: Average production.

Source: Authors

Results and discussion

The model was run with a three-objective function: a) only the time component of equation (1); b) only the cost component of Equation (1), –in these case, to be minimized–, and c) the complete equation (1). The results obtained from the 155 generated instances are presented in Table 5. Additionally, the option of relaxing constraints (11) and (12) related to the minimum and maximum production levels was considered (i.e. “without bounds” in Table 5).

Table 5. Numerical experimentation results

	# washing procedures	Unmet demand (%) with respect to:		% instances according CPU time
		# products	Volume	≤ 1 min	1-5 min	≤ 30 min
Without bounds ¨Min time ¨Min cost ¨Max profit	175 124 155	39 % 45 % 40 %	14 % 16 % 22 %	80 100 100	20 0 0	0 0 0
With bounds ¨Min time ¨Min cost ¨Max profit	250 215 203	25 % 18 % 27 %	2 % -1 % 6 %	80 100 100	0 0 0	0 0 0

Source: Authors

From Table 5, it can be seen that the vast majority of instances were resolved in less than one minute; however in the case of minimizing time with quotas, 20 % of instances could not be resolved in half an hour. A much better performance in terms of demand compliance is also observed when considering the bounds constraints; but a better performance in terms of number of washing procedures is shown when these are not included. The negative unmet demand value refers to an average production of 1 % above the reorder point. Finally, no objective function is dominant in terms of performance.

Conclusions

The problem of a single machine production system with sequence dependent setup times and several real world operational constraints was studied.

A comparative performance study between the mathematical model and real data from a chemical company was carried out, obtaining the following results with the proposed model: a reduction of 2 % in the processing time of the product, a 12 % reduction in the total cost of production and an increase of 19 % in the estimated profit. The optimization model allows the integration of the decision about the order of the products to be processed in the different production machines, the number of batches to produce each item, the time each product will start to be processed and other decisions that seek to quantify non-compliance with respect to demand and due dates. Finally, through Monte Carlo simulation, instances were generated to validate the model, obtaining solutions in short computational times in a desk computer (i.e. half an hour) for sizes similar to those of the industry.

Acknowledgements

The authors thank the engineers Felipe Andrés Sánchez Batallas for his participation in the programming of the interface, Walter Valderrama and Emilio Ruiz Sámano for their participation in numerical experimentation.

References

Afzalirad, M., & Rezaeian, J. (2016). Resource-constrained unrelated parallel machine scheduling problem with sequence dependent setup times, precedence constraints and machine eligibility restrictions. Computers & Industrial Engineering, 98, 40–52.

Allahverdi , A., Ng, C. T., Cheng, T., & Kovalyov, M. Y. (2008). A survey of scheduling problems with setup times or costs. European Journal of Operational Research, 187, 48. DOI:10.1016/j.ejor.2006.06.060

Atan, M. O., & Akturk, M. S. (2008). Single CNC machine scheduling with controllable processing times and multiple due dates. International Journal of Production Research, 46. DOI:10.1080/00207540701262913

Castro, P. M., & Novais, A. Q. (2009). Scheduling multistage batch plants with sequence-dependent changeovers. American Institute of Chemical Engineers AIChE Journal. 55, 8: 2122-2137. DOI: 10.1002/aic.11799.

Chang, Y.-L., & Manikas, A. (2009). A scatter search approach to sequence-dependent setup times job shop scheduling. International Journal of Production Research, 47, 21. DOI:10.1080/00207540701805646

Chen, H., Zuo, L., Wu, C., Wang, L., Diao, F., Chen, J., & Huang, Y. (2017). Optimizing detailed schedules of a multiproduct pipeline by a monolithic MILP formulation. Journal of Petroleum Science and Engineering, 159, 148- 163. DOI:10.1016/j.petrol.2017.09.036

Dutta, G., Gupta, N., & Fourer, N. (2011). An optimization-based decision support system for strategic planning in a process industry: the case of aluminium company in India. Journal of the Operational Research Society, 62, 11. DOI:10.1057/jors.2010.8

Harjunkoski, I., Maravelias, C. T., Bongers, P., Castro, P. M., Engell, S., Grossmann, I. E., . . . Wassick, J. (2014). Scope for industrial applications of production scheduling models and solution methods. Computers and Chemical Engineering 62 (2014), 62, 161–193.

Hassin, R., & Shani, M. (2005). Machine scheduling with earliness, tardiness and non-execution penalties. Computers & Operations Research, 32, 683 – 705.

He, Y., & Hui, C.-W. (2008). A rule-based genetic algorithm for the scheduling of single-state multi-product batch plants with parallel units. Computers and Chemical Engineering, 32, 3067-3083. DOI:10.1016/j.compchemeng.2008.04.008

Hinder, O., & Mason, A. (2017). A novel integer programming formulation for scheduling with family setup times on a single machine to minimize maximum lateness. European Journal of Operational Research, 262, 411-423. DOI:10.1016/j.ejor.2017.03.003

Jans, R., & Degraeve, Z. (2008). Modeling industrial lot sizing problems: a review. International Journal of Production Research, 46, 26. DOI:10.1080/00207540600902262

Jin, F., Gupta, J., Song, S., & Wu, C. (2010). Single machine scheduling with sequence-dependent family setups to minimize maximum lateness. Journal of the Operational Research Society, 61(7), 1181–1189.

Karimi, B., Ghomi, S. F., & Wilson, J. M. (2003). The capacitated lot sizing problem: a review of models and algorithms. The International Journal of Management Science, 31, 14. DOI:10.1016/S0305-0483(03)00059-8

Karimi, I., & Liu, Y. (2005). A continuous-time formulation for scheduling multi-stage multi-product batch plants with non-identical parallel units. Computer Aided Chemical Engineering, 20, 1165-1170.

Koçlar, A. (2005). The general lot sizing and scheduling problem with sequence dependent changeovers.

Liu, Y., & Karimi, I. A. (2005). A Continuous-Time Formulation for Scheduling Multi-Stage Multi-product Batch Plants with Non-identical Parallel Units. European Symposium on Computer Aided Process Engineering, 15, 6.

Marchetti, P., & Cerdá, J. (2009). An approximate mathematical framework for resource-constrained multistage batch scheduling. Chemical Engineering Science, 64, 2733–2748.

McGraw, K. E., & Dessouky, M. M. (2001). Sequence-dependent batch chemical scheduling with earliness and tardiness penalties. International Journal of Production Research, 39, 23. DOI:10.1080/00207540110056180

Mendez, C. A., Cerdá, J., Grossmann, I. E., Harjunkoski, I., & Fahl , M. (2006). State-of-the-art review of optimization methods for short-term scheduling of batch processes. Computers and Chemical Engineering, 30, 34. DOI:10.1016/j.compchemeng.2006.02.008

Mendez, C., Henning, G., & Cerda, J. (2000). Optimal scheduling of batch plants satisfying multiple product orders with different due-dates. Computers & Chemical Engineering, 24(9-10), 2223-2245.

Merchan, A. F., Lee, H., & Maravelias, C. T. (2016). Discrete-time mixed-integer programming models and solution methods for production scheduling in multistage facilities. Computers and Chemical Engineering 94 (2016) 387–410, 94, 387–410.

Nekoiemehr , N., & Moslehi, G. (2011). Minimizing the sum of maximum earliness and maximum tardiness in the single-machine scheduling problem with sequence-dependent setup time. Journal of the Operational Research Society, 62, 10. DOI:10.1057/jors.2010.94

Novara, F. M., Novas, J. M., & Henning, G. (2016). A novel constraint programming model for large-scale scheduling problems in multiproduct multistage batch plants: Limited resources and campaign-based operation. Computers and Chemical Engineering, 39, 101-117.

Omar, M. K., & Teo, S. C. (2006). Minimizing the sum of earliness/tardiness in identical parallel machines schedule with incompatible job families: An improved MIP approach. Applied Mathematics and Computation, 181,(2), 1008-1017.

Osorio G., J. C., Castrillón M., O. E., Toro C., J. A., & Orejuela C, J. P. (2008). Hierarchical production planning model in flexible job shop including a preemption and sequence-dependent setup times. Ingeniería e Investigación, 28(2), 72-79.

Subbiah, S., Tometzki, T., Panek, S., & Engell, S. (2009). Multi-product batch scheduling with intermediate due dates using priced timed automata models. Computers and Chemical Engineering, 33, 1661-1676. DOI:10.1016/j.compchemeng.2009.05.007

Transchel, S., Minner, S., Kallrath, J., Löhndorf, N., & Eberhard, U. (2011). A hybrid general lot-sizing and scheduling formulation for a production process with a two-stage product structure. International Journal of Production Research, 49, 19. DOI:10.1080/00207543.2010.532910

Tsai, W., & Wang, C.-H. (2017). Extended economical maintenance scheduling for a batch production system. Journal of Information and Optimization Sciences, 38(2), 219-231.

Velez, S., Dong, Y., & Maravelias, C. T. (2017). Changeover formulations for discrete-time mixed-integer programming scheduling models. European Journal of Operational Research, 260, 949-963.

>Xue, Y.-F., & Sun, H.-L. (2010). An effective formulation for optimal scheduling of multistage multi-product batch plant based on due dates. International Journal of Production Research, 48, 14. DOI:10.1080/00207540802534681

Zeballos, L., Novas, J., & Henning, G. (2011). A CP formulation for scheduling multiproduct multistage batch plants. Computers and Chemical Engineering, 35, 2973-2989.

Attribution 4.0 International (CC BY 4.0) Share - Adapt