Conceptual analysis of single-feed heterogeneous distillation columns
Análisis conceptual de columnas de destilación heterogénea con un alimento
DOI:
https://doi.org/10.15446/ing.investig.v35n2.49247Palabras clave:
VLL equilibrium, heterogeneous azeotropic distillation, operation leaves, pinch point curves, conceptual analysis (en)Equilibrio VLL, destilación azeotrópica heterogénea, hojas de operación, curvas pinch, análisis conceptual. (es)
Descargas
Separation in heterogeneous distillation columns is attained by interaction of two liquid and one vapor phases, interaction of three phases involves complexities due to the determination of vapor-liquid-liquid equilibrium and hence, in the design of separation units. Nevertheless, the liquid-liquid equilibrium allows developing separations that may be unfeasible by vapor-liquid equilibrium. In this way, heterogeneous azeotropic distillation is a useful operation for the separation of azeotropic and close-boiling mixtures. In this work, a new methodology for evaluating the feasibility of this process is developed. This methodology is an extension of that proposed by Castillo et al. (1998) for homogeneous systems. Operation leaves for heterogeneous systems are calculated using the concept of pinch point curves in order to establish the process feasibility. Heterogeneous columns with external decanter are considered as the only heterogeneous stage (OHED: only heterogeneous external decanter). The initialization process for the column calculation requires the selection of the distillate composition using thermodynamic criteria in order to guarantee homogeneous phases within the column. A system with industrial and academic relevance was considered as case study: water-acetic acid-amyl acetate. Results show that the developed shortcut method allows evaluating process feasibility and estimating design parameters, without the use of trial and error procedures implemented, with the aid of simulation tools.
En las columnas de destilación heterogénea la separación se logra por la interacción de dos fases líquidas y una de vapor, la interacción de tres fases genera complejidades especiales en los cálculos de equilibrio vapor-líquido-líquido y de los equipos de separación que se basan en este equilibrio; sin embargo, el equilibrio líquido-líquido permite desarrollar separa-ciones que pueden ser imposibles mediante equilibrio vapor-líquido. En este sentido, la destilación azeotrópica heterogénea es una operación útil para la separación de mezclas azeotrópicas y con puntos de ebullición cercanos. En este trabajo se desarrolla una nueva metodología para evaluar la viabilidad de este proceso de separación; esta metodología es una extensión de la propuesta por Castillo et al. (1998) para sistemas homogéneos. Las hojas de operación se calculan usando el concepto de curvas pinch para establecer la viabilidad del proceso. Las columnas heterogéneas con decantador externo fueron consideradas como la única etapa heterogénea (OHED: only heterogeneous external decanter). Para iniciar el cálculo de las columnas es necesario escoger la composición del destilado con criterios termodinámicos, para garantizar que la fase líquida es homogénea en la columna. Un sistema con relevancia académica e industrial fue considerado como estudio de caso: agua-ácido acético-acetato de amilo. Los resultados muestran que el método corto desarrollado permite determinar la viabilidad del proceso y estimar parámetros de diseño, evitando la implementación de procedimientos de ensayo y error con el auxilio de herramientas de simulación.
Conceptual analysis of single-feed heterogeneous
distillation columns
Análisis conceptual de columnas de destilación heterogénea
con un alimento
L. Estupiñan1, and C. A. M. Riascos2
1 Libardo Estupiñan Perez. Chemical Engineer, M.Sc., Universidad Nacional de Colombia. Colombia. Affiliation: Ph.D Student, University of Alberta, Canada. E-mail: estupina@ualberta.ca.
2 Carlos Arturo Martinez Riascos. Chemical Engineer, Ph.D. Universidade de São Paulo, Brasil. Affiliation: Associated Professor, Universidad Nacional de Colombia, Colombia. E-mail: camartinezri@unal.edu.co.
How to cite: Estupiñan, L., & Martínez, C. A. (2015). Conceptual analysis of single-feed heterogeneous distillation columns. Ingeniería e Investigación, 35(2), 36-42. DOI: https://doi.org/10.15446/ing.investig.v35n2.49247
ABSTRACT
Separation in heterogeneous distillation columns is attained by interaction of two liquid and one vapor phases, interaction of three phases involves complexities due to the determination of vapor-liquid-liquid equilibrium and hence, in the design of separation units. Nevertheless, the liquid-liquid equilibrium allows developing separations that may be unfeasible by vapor-liquid equilibrium. In this way, heterogeneous azeotropic distillation is a useful operation for the separation of azeotropic and close-boiling mixtures. In this work, a new methodology for evaluating the feasibility of this process is developed. This methodology is an extension of that proposed by Castillo et al. (1998) for homogeneous systems. Operation leaves for heterogeneous systems are calculated using the concept of pinch point curves in order to establish the process feasibility. Heterogeneous columns with external decanter are considered as the only heterogeneous stage (OHED: only heterogeneous external decanter). The initialization process for the column calculation requires the selection of the distillate composition using thermodynamic criteria in order to guarantee homogeneous phases within the column. A system with industrial and academic relevance was considered as case study: water-acetic acid-amyl acetate. Results show that the developed shortcut method allows evaluating process feasibility and estimating design parameters, without the use of trial and error procedures implemented, with the aid of simulation tools.
Keywords: VLL equilibrium, heterogeneous azeotropic distillation, operation leaves, pinch point curves, conceptual analysis.
RESUMEN
En las columnas de destilación heterogénea la separación se logra por la interacción de dos fases líquidas y una de vapor, la interacción de tres fases genera complejidades especiales en los cálculos de equilibrio vapor-líquido-líquido y de los equipos de separación que se basan en este equilibrio; sin embargo, el equilibrio líquido-líquido permite desarrollar separaciones que pueden ser imposibles mediante equilibrio vapor-líquido. En este sentido, la destilación azeotrópica heterogénea es una operación útil para la separación de mezclas azeotrópicas y con puntos de ebullición cercanos. En este trabajo se desarrolla una nueva metodología para evaluar la viabilidad de este proceso de separación; esta metodología es una extensión de la propuesta por Castillo et al. (1998) para sistemas homogéneos. Las hojas de operación se calculan usando el concepto de curvas pinch para establecer la viabilidad del proceso. Las columnas heterogéneas con decantador externo fueron consideradas como la única etapa heterogénea (OHED: only heterogeneous external decanter). Para iniciar el cálculo de las columnas es necesario escoger la composición del destilado con criterios termodinámicos, para garantizar que la fase líquida es homogénea en la columna. Un sistema con relevancia académica e industrial fue considerado como estudio de caso: agua-ácido acético-acetato de amilo. Los resultados muestran que el método corto desarrollado permite determinar la viabilidad del proceso y estimar parámetros de diseño, evitando la implementación de procedimientos de ensayo y error con el auxilio de herramientas de simulación.
Palabras clave: Equilibrio VLL, destilación azeotrópica heterogénea, hojas de operación, curvas pinch, análisis conceptual.
Received: February 17th 2014
Accepted: May 26th 2015
Introduction
Separation of heterogeneous systems by distillation is a common operation in industry since it takes advantage of partial miscibility properties to achieve the separation of an azeotropic mixture. Although it is a useful operation, heterogeneous distillation has not received quite attention in the conceptual design due to its complexity. Taylor (2007) presented a state of art paper on distillation and absorption modelling where it is evident that three-phase distillation remains relatively poor understood when compared to distillation with a single liquid phase. The main reason for this is the difficulty of modelling more than one liquid phase throughout the distillation column.
Pham et al. (1989) and Van Dongen and Doherty (1985) presented a methodology based on the boundary value method (BVM) to calculate both distillation profiles and minimum reflux in single-feed columns. While the work of Van Dongen and Doherty (1985) was focused on homogenous distillation, the work of Pham et al. (1989) described the problem for heterogeneous distillation. The method was developed taking into account two important assumptions: 1) constant molar overflow (CMO) and 2) partial miscibility only considered in condenser and decanter; therefore, the distillation column operates in the homogeneous region. For nonideal mixtures, the first consideration is not very accurate, but for conceptual design, it can be accepted. As for the second assumption, modelling of separation processes in heterogeneous systems is easier when the column is operated in the homogeneous region (Prayoonyong and Jobson, 2011; Urdaneta et al., 2002) because heterogeneous phases generate a multiparametric design problem. Hence, columns in which the only heterogeneous stage is the decanter are more efficient and easier to control in practice (Pham and Doherty, 1990b). However, this constraint requires a careful selection of the overhead vapor at the top of the column.
The most recent studies in heterogeneous systems have been focused on the determination of minimum reflux using methods developed for homogeneous systems. Kraemer et al. (2011) presented two novel shortcut methods: the feed pinch method (FPM) and the feed angle method (FAM). The FAM is based on the method proposed by Koehler et al. (1991). FAM is suitable for direct, indirect, and intermediate splits. It also takes conceptual elements from other methods such as zero volume criteria (Julka and Doherty, 1990) and Petlyuk’s methodology (Petlyuk, 2004). FPM is faster than FAM since it does not require tray by tray calculation, but it involves to perform a pinch analysis using the Rectification Body Method (RBM) in the initialization process, and the shortest stripping line method in order to determine the relevant pinch points such as tangent pinches or the initial value for the minimum energy demand. The main advantage of FAM is the ability to solve columns with different types of splits.
Królikowski et al. (2011) studied the behavior of the rectifying profiles in heterogeneous systems with distillation boundaries. Furthermore, the pitchfork boundary analysis was extended to heterogeneous systems. The study showed that the topological behavior between heterogeneous and homogeneous systems is analog. Differences can be observed in the parametric sensibility presented in systems with partial miscibility.
As mentioned above, different methods for the analysis of heterogeneous distillation have been reported in specialized literature. In this paper, a method to evaluate the feasibility in single-feed heterogeneous columns is proposed. The method is based on the ideas presented in our previous works (Estupiñan Perez et al., 2011 and 2015) where both pinch point curves and reversible distillation concepts are the foundations. Pinch point curves are used in heterogeneous systems along with residue curves and phase equilibrium analysis in order to evaluate process feasibility employing the operation leaves (Castillo et al., 1998). Phase equilibrium calculation for heterogeneous systems used to be performed using material stability analysis. In this work, an alternative and less complex strategy, based on the knowledge of the partial miscibility region, is presented. Using the tools abovementioned altogether, a method able to assess the process feasibility in single-feed heterogeneous distillation becomes a practical alternative for the analysis of separation systems with partial miscibility.
Heterogeneous column model
In addition to the assumptions made in the BVM for homogeneous columns, the model for heterogeneous systems is based on the fact the column is operated within the homogeneous region. Therefore, there is only one heterogeneous stage in the unit, the decanter. A strategy that guarantees that the separation unit operates in the homogeneous region was developed by Pham et al. (1989) and is used in this work.
Since the column operates in the homogeneous region, its equations are the same as those for homogeneous columns. The difference between the BVM for homogeneous and heterogeneous systems is the initialization process that must be carried out in the rectifying section for heterogeneous systems in order to ensure that the column will operate in the homogeneous region. On the other hand, constant molar flow (CMO) assumption was taken into account; although this assumption is not accurate for highly nonideal mixtures, it was used in this work as the main focus is a simplified methodology to evaluate the process feasibility. Further, the geometrical features presented by heterogeneous systems are another important focus in this work. To illustrate model variables, a schematic for the column is shown in Figure 1.
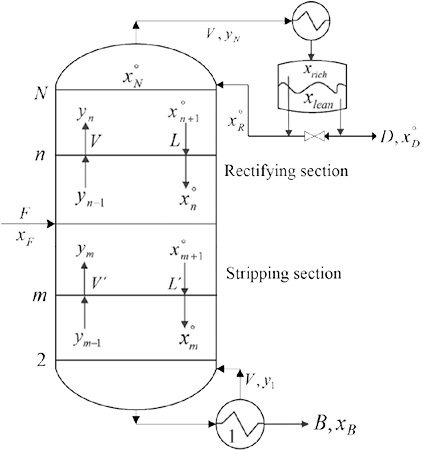
Figure 1. Schematic representation of a heterogeneous distillation column.
Considering two liquid phases, Lα and Lβ, and defining an overall liquid flow into the column, L = Lα + Lβ, and its fraction, x°J , 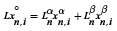 , the mass balance around the n-th plate in the rectifying section generates:
, the mass balance around the n-th plate in the rectifying section generates:
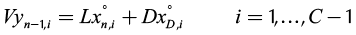 (1)
(1)
where C corresponds to the number of components in the mixture. Therefore, the equations for the rectifying and stripping sections are the same as those for single feed homogeneous columns:
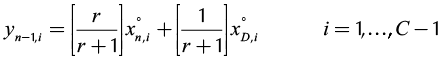 (2)
(2)
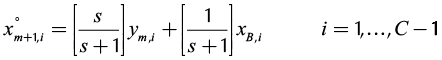 (3)
(3)
In addition to the section column equations, the reflux (r) and reboil (s) ratios are related in the same way as those of the homogeneous columns (Levy et al., 1985).
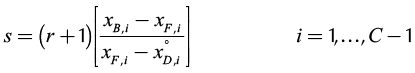 (4)
(4)
Although in this model equations for both heterogeneous and homogeneous columns are the same, profiles calculation is different, especially for the rectifying section where the initialization process requires the knowledge of thermodynamic and topologic mixture behavior. Hence, it is necessary to determine accurately the partial miscibility region and the composition of the azeotropes. Apart from the model equations presented above, another variable should be defined for heterogeneous columns: the overhead vapor is totally condensed, it will form two immiscible liquid phases in the decanter, one of them will be an entrainer-rich phase of composition χrich and the other liquid phase will be an entrainer-lean phase of composition χlean. As a result, a new variable, ϕ, must be defined in order to calculate the relative proportion of these two liquid phases in the decanter. The relative proportion can be obtained through the lever rule, as follows (Pham and Doherty, 1990b):
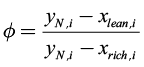 (5)
(5)
The ratio ϕ is an important design variable in heterogeneous columns since it provides the values for both distillate and reflux streams. Pham and Doherty (1990b) considered two possible reflux ratios to configure the decanter: r ≥ ϕ and r ≤ ϕ. At r ≥ ϕ the reflux rate is greater than the condensation rate of entrainer-rich phase. This condition implies that the distillate stream is only a fraction of the entrainer-lean phase, and the reflux stream includes all the entrainer-rich phase plus the remaining fraction of the entrainer-lean phase. Therefore, this policy allows manipulating the reflux ratio keeping the distillate composition. When r is fixed, the composition of the reflux stream (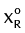 ) is defined.
) is defined.
The second reflux policy, r ≤ ϕ, does not allow to manipulate the reflux ratio and composition as in the case explained above. In this case, the reflux rate is less than the condensation rate of entrainer-rich phase, i.e., the reflux stream 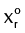 consists of a fraction of entrainer-rich phase. In addition, this policy requires that the distillate rate be greater than condensation rate of entrainer-lean phase; thus, the distillate stream consists of all the entrainer-lean phase plus the balance of the entrainer-rich phase. Accordingly, there is a unique value of r that satisfy the column mass balances. Geometrically, mass balances are verified by the collinearity between
consists of a fraction of entrainer-rich phase. In addition, this policy requires that the distillate rate be greater than condensation rate of entrainer-lean phase; thus, the distillate stream consists of all the entrainer-lean phase plus the balance of the entrainer-rich phase. Accordingly, there is a unique value of r that satisfy the column mass balances. Geometrically, mass balances are verified by the collinearity between 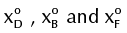 .
.
Methodology for conceptual analysis
Phase equilibrium calculation
One of the main challenges in heterogeneous distillation is to determine the number of phases under specific conditions of temperature, pressure and composition. Due to the changes in composition throughout the distillation column, it is necessary to verify the number of phases in equilibrium in each column stage. Robust algorithms such as tangent plane criteria (Michelsen, 1982) have been proposed to determine the number of phases present in a mixture. A shortcoming of this method and in general of all methods based on Gibbs free energy minimization is the long computation time as well as the complex programming. Besides, after the material stability analysis is performed, it is required to calculate the phase equilibrium with the predicted number of phases.
Due to the fact that stability analysis adds complexity and computation time, a simpler strategy to solve the phase equilibrium calculation is presented. The strategy is based on the knowledge of heterogeneous regions. For this purpose, it is necessary to calculate the binodal curve that delimits homogeneous and heterogeneous regions. Continuation methods (Sánchez et al., 2010; Sanchez et al., 2013; Estupiñan et al., 2015) were used to determine the binodal curve. For a mixture of C components, the system of 3C + 3 equations that represent the binodal curve and the vapor line is:
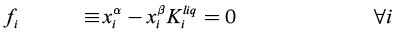 (6)
(6)
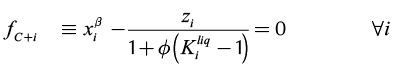 (7)
(7)
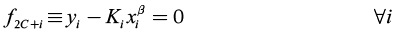 (8)
(8)
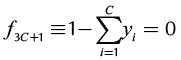 (9)
(9)
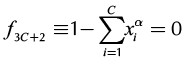 (10)
(10)
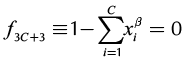 (11)
(11)
where superscripts α, β represent the liquid phases in the mixture. Variables are grouped in a vector:
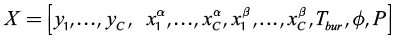 (12)
(12)
The solution determines the VLL binodal along with the vapor line as shown in Figure 2. Using the knowledge on the heterogeneous region, it is possible to determine the number of phases present in each column stage. Therefore, when distillation profiles, residue and pinch curves are calculated, the model for phase equilibrium calculation must change depending on the region that the profile is crossing. Furthermore, the methodology calculates the complete vapor line that, as considered later, is essential for the design process.
After the calculation of the binodal curve, phase equilibrium calculation must be performed to determine the composition of each phase. For VLLE calculation in heterogeneous systems, a modification of the Rachford and Rice algorithm for vapor-liquid calculations (Henley and Seader, 1981) was employed, which is based on the principle of chemical potential equality at the equilibrium state; thus, at the condition of VLLE, three phases coexist (V: vapor, : liquids) and the chemical potential constraint is:
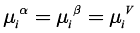 (13)
(13)
Solution strategy for distillation profiles
As mentioned above, the calculation of rectifying profiles requires a different initialization process for heterogeneous columns to guarantee the distillation column will operate in the homogeneous region. The knowledge of partial miscibility region is essential in this process step. For instance, the thermodynamic description for water-acetic acid-amyl acetate system was carried out and is shown in Figure 2. This calculation was performed in Matlab, using the NRTL model (Renon and Prausnitz, 1968) for liquid phase and the Marek’s method (Sebastiani and Lacquaniti, 1967) for vapor phase, in order to take into account the acetic acid dimerization. In this system, the mixture to be separated is water-acetic acid, and amyl acetate is considered as entrainer in order to achieve the required acid purity.
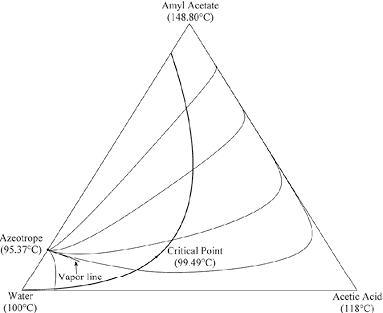
Figure 2. Topological behavior of water-acetic acid-amyl acetate system at 1bar. Residue curves, partial miscibility region, and vapor line.
In addition to the partial miscibility region, the vapor line is important for the design of heterogeneous columns due to its thermodynamic implication: each point on the vapor line is in vapor-liquid-liquid equilibrium (VLLE). However, the column model performs calculations in distillation columns in which the only heterogeneous stage is the decanter. Hence, it is necessary for the overhead vapor to be in equilibrium with a homogeneous liquid, which corresponds to the liquid on the top tray of the column (x°N ). As a result, the overhead vapor (yN) should be chosen as a point inside the miscibility region, but not on the vapor line. Compositions in Figure 3 depict the material balance line in an heterogeneous column with the features mentioned above, this material balance corresponds to the cases r > ϕ or r = ϕ. Therefore, the composition of the distillate (xD) is equal to the entrainer-lean phase (xlean). Besides, the selection of the overhead vapor (yN) must be carefully carried out in order to guarantee the separation feasibility.
As has been described so far, initialization of rectifying profiles requires to specify some variables and to know the thermodynamic features of the mixture. The first step is based on the knowledge of the miscibility region and involves the selection of a tie line for the decanter. Here, two factors must be taken into account: 1) the reflux policy r ≥ ϕ implies that xlean is equal to xD and, 2) The tie line should be located in the correct distillation region according to the specified bottom product. The second step requires the specification of the overall material balance line, which is determined by xD, F and xB.
In the third step, the overhead vapor composition (yN) is specified, its composition must be on the tie line but not on the vapor line. Furthermore, yN must be located in the same distillation region of xB, which guarantees that rectifying and stripping profiles can intersect each other and hence, the distillation process becomes feasible. This consideration is irrelevant for systems like water-acetic acid-amyl acetate where the topologic thermodynamic points out the absence of distillation boundaries (Figure 2). However, in systems with distillation boundaries, e.g., ethanol-water-benzene analyzed in Estupiñan (2012), this consideration is fundamental for the conceptual analysis.
Having defined the ϕ compositions in the previous steps, in the next step the ϕ variable should be calculated (Equation 5). Subsequently, in the fifth step it is possible to specify a reflux ratio value taking into account the design condition r≥ ϕ.
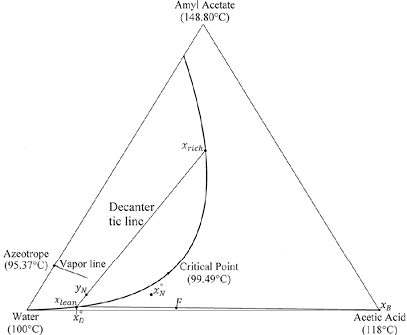
Figure 3. Design specification, mass balance constraint and partial miscibility region for water-acetic acid-amyl acetate system.
Finally, the design specifications are fulfilled when the reboil ratio (s) is calculated from Equation 4. In this way, after the process to determine the initial point in each profile is completed, the calculations for both rectifying and stripping profiles are estimated with the same methodology used for single feed homogeneous columns (Van Dongen and Doherty (1985), Levy et al. (1985), Estupiñan et al. (2015)). Therefore, the first calculation in the rectifying section should be a dew point calculation in order to determine the liquid composition (x°N ) in equilibrium with the overhead vapor. After that, rectifying profile (Equation 2) is solved until the profile reaches its fixed point. It is important to mention that the calculation of the rectifying profile implies the calculation of the liquid-vapor equilibrium at each point on the profile. For the stripping profile, the calculation is the same as in homogeneous systems. The design specifications for water-acetic acid-amyl acetate along with its topological features are depicted in Figure 3.
Operation leaves calculation
Operation leaves are formed by pinch point curves and residue curves. The operation leaf delimits all possible operation profiles after specification of feed, and distillate and bottom products. Each column section has one operation leaf that should overlap the other section leaf for the design to be feasible (Castillo et al., 1998). Therefore, to construct an operation leaf is necessary to specify one product either bottoms or distillate, and feed composition. Using continuation methods along with the procedure to determine the number of phases it was possible to develop a method for calculating these curves and tracing out operation leaves in heterogeneous systems. Calculation methodology is similar to that for homogeneous systems; main differences are based on the complexity of the correct description of phase equilibrium and the number of phases. The system of equations that describe a pinch point in a heterogeneous region is bigger than that for homogeneous system. Therefore, for a three components system, in heterogeneous regions 14 (4C + 2) equations are needed to complete the description of a pinch point and phase equilibrium. The system of equations for the stripping section is shown as follows:
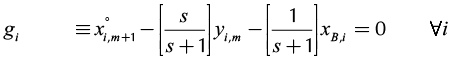 (14)
(14)
 (15)
(15)
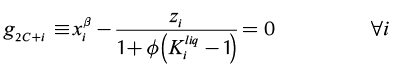 (16)
(16)
 (17)
(17)
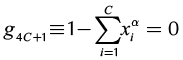 (18)
(18)
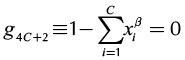 ( 19)
( 19)
Equations 16 and 17 represent the liquid-liquid equilibrium. The remaining equations describe column section profile, vapor-liquid equilibrium and molar fraction summation. For the rectifying section, Equation 14 should be changed by its respective expression obtained from Equation 2. Furthermore, it is important to mention that the equations described above must be only used in the heterogeneous region. For homogeneous region, the calculation is carried out as presented in a previous work (Estupiñan et al., 2015). Before applying the continuation method, the equations and variables are grouped as follows:
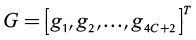 (20)
(20)
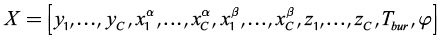 (21)
(21)
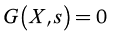 (22)
(22)
The knowledge of the heterogeneous region allows identifying the transition of phases, i.e., the point where the number of phases change. In this point, the calculation algorithm should be changed and the next pinch point is calculated using the algorithm for homogeneous systems. Stripping and rectifying curves are traced out until they reach constant composition points. These points are the initial values to calculate the residue curves.
For residue curves calculation, the algorithm presented by Pham and Doherty (1990a) with the proposed methodology to determine the heterogeneous region was employed. The equation for residue curves is shown below:
 (23)
(23)
where τ is a dimensionless time. When Equation 23 is numerically integrated, heterogeneous residue curves are obtained. Figure 4 describes the algorithm for the feasibility analysis.
Illustrative example
In order to apply the proposed methodology and demonstrate its usefulness in the determination of the process feasibility, the system water-acetic acid-amyl acetate was chosen as case study due to its topological, thermodynamics features, and industrial relevance. Although water-acetic acid mixture does not form azeotropes, its separation is difficult since it is a close-boiling mixture. Acetic acid separation from mixtures with water is possible to achieve using heterogeneous azeotropic distillation. Amyl acetate forms a partial miscibility region and a minimum boiling point azeotrope with water as can be seen in Figure 2. The application of the proposed methodology in other ternary systems, e.g., ethanol-water-benzene is presented in Estupiñan (2012).
Operation leaves for water-acetic acid-amyl acetate mixture were traced out and are depicted in Figure 5. Stripping and rectifying operation leaves are one next to the other since this system does not have distillation boundaries. Despite the absence of distillation boundaries, to achieve a suitable process design for obtaining high purity acetic acid is not a simple task since it requires to locate the overhead vapor (yN) on a correct location on the decanter tie line. It must be taken into account that this composition cannot be on the vapor line due to the fact that it will cause two liquid phases in the distillation column, since the liquid on the top tray of the column (x°N ) is in equilibrium with overhead vapor, hence (x°N ) must be outside of the partial miscibility region.
As mentioned above, composition of overhead vapor (yN) is a degree of freedom and its location will determine the column operation region and the process feasibility. To obtain a feasible design operation leaves of each column section should overlap and hence, the separation is possible. As shown in Figure 5, the selected overhead vapor composition (yN) allows obtaining acetic acid as the bottom product with a purity of 99.9% and as distillate (x°D ) a ternary mixture, mostly water. Finally, for a feasible design, the collinearity condition for F, x°D and B must be verified in order to satisfy the global mass balance. The illustrative example showed that the shortcut method developed for evaluating the process feasibility in heterogeneous single-feed distillation provide accurate results and the initial design parameters for the rigorous simulation.
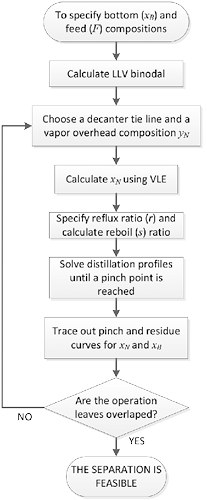
Figure 4. Algorithm for the analysis of process feasibility.
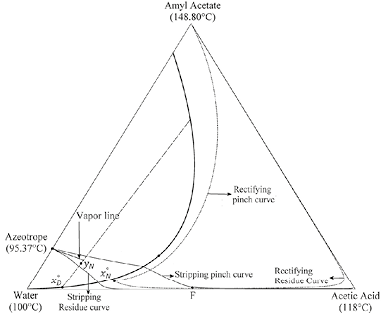
Figure 5. Operation leaves for water-acetic acid-amyl acetate.
Conclusions
The concept of operation leaves was successfully extended, from our previous work on homogeneous systems to heterogeneous mixtures for distillation columns with only heterogeneous external decanter. According to the obtained results, it is clear that OHED operation policy is efficient, since the desired separation is achieved. A simpler algorithm to calculate phase equilibrium without the necessity of material stability analysis was used. The algorithm uses continuation methods to calculate the vapor-liquid-liquid binodal curve. With the precise delimitation of the heterogeneous region, it was possible to determine the phase equilibrium, which should be used when pinch and residue curves are calculated.
The presented methodology allows evaluating the feasibility of a specific separation task. When products and feed stream are fixed, the feasibility can be evaluated through the operation leaves concept. For the study case, it is evident that the separation of the main component (acetic acid) is accomplished under this operation conditions. One of the main advantages of this method is the gaining of knowledge about the thermodynamic and topological behavior of the system. On the other hand, the conceptual design avoids using commercial simulators to determine process feasibility and estimating design parameters. Instead, commercial simulators can be used as a complement of the conceptual design in order to evaluate the process performance with the parameters calculated by the shortcut method.
Finally, it is clear that heterogeneous azeotropic distillation is more sensitive to the initial parameters when compared to homogeneous azeotropic distillation. Therefore, to guarantee that heterogeneous process is successful, the accurate specification of variables such as the vapor overhead (yN) is required. Although process synthesis is difficult, the conceptual design, based on thermodynamic features, allows determining the exact and convenient point where yN must be located and approximated values for reflux and reboil ratios. Without these tools, the design process would be more complex, and hence, it would require extensive parametric studies in order to calculate the design parameters.
References
Castillo, F.J.L., Thong, D.Y., & Towler, G.P. (1998). Homogeneous Azeotropic Distillation. 1. Design Procedure for Single-Feed Columns at Nontotal Reflux. Industrial & Engineering Chemistry Research 37(3), 987-997.
DOI: 10.1021/ie970480b.
Estupiñán, L. (2012). Tools development for analysis and conceptual design of extractive and azeotropic distillation columns at finite reflux. MSc Thesis Universidad Nacional de Colombia.
Estupiñan, L., Sánchez, C.A., Riascos, C.A.M, & Arturo Calvache, J. (2011). Análisis de las Posibilidades de Separación en Columnas de Destilación Azeotrópica Homogénea Operando a Reflujo Finito, Proceedings of XXVI Colombian Congress of Chemical Engineering.
Estupiñan Perez, L., Dechaine, G, P., & Riascos, C.A.M. (2015). Simplified Conceptual Design Methodology for Double-Feed Extractive Distillation Processes. Ind. Eng. Chem. Res., 54 (20), pp 5481–5493. DOI: 10.1021/ie501781p.
Henley, E.J., & Seader, J.D. (1981). Equilibrium-Stage Separation Operations in Chemical Engineering. New York: J. Wiley.
Julka, V., & Doherty, M.F. (1990). Geometric behavior and minimum flows for nonideal multicomponent distillation. Chemical Engineering Science 45(7), 1801-1822
Koehler, J., Aguirre, P., & Blass, E. (1991). Minimum Reflux Calculations for Nonideal Mixtures using the Reversible Distillation Model. Chemical Engineering Science 46(12), 3007-3021. DOI: 10.1016/0009-2509(91)85005-I.
Kraemer, K., Harwardt, A., Skiborowski, M., Mitra, S., Marquardt, & W. (2011). Shortcut-based design of multicomponent hetero-azeotropic distillation. Chemical Engineering Research and Design 89(8), 1168-1189.
DOI: 10.1016/j.cherd.2011.02.026.
Królikowski, A.R., Królikowski, L.J., & Wasylkiewicz, S.K. (2011). Distillation profiles in ternary heterogeneous mixtures with distillation boundaries, Chemical Engineering Research and Design 89(7), 879-893.
DOI: 10.1016/j.cherd.2010.11.016.
Levy, S.G., Van Dongen, D.B., & Doherty, M.F. (1985). Design and synthesis of homogeneous azeotropic distillations. 2. Minimum reflux calculations for nonideal and azeotropic columns. Industrial & Engineering Chemistry Fundamentals 24(4), 463-474. DOI: 10.1021/i100020a011.
Michelsen, M.L. (1982). The isothermal flash problem. Part I. Stability, Fluid Phase Equilibria 9(1), 1-19.
DOI: 10.1016/0378-3812(82)85001-2.
Petlyuk, F.B. (2004). Distillation Theory and its Application to Optimal Design of Separation Units. Cambridge, U.K: Cambridge University Press.
DOI: 10.1017/CBO9780511547102.
Pham, H.N., & Doherty, M.F. (1990a). Design and synthesis of heterogeneous azeotropic distillations—II. Residue curve maps. Chemical Engineering Science 45(7), 1837-1843. DOI: 10.1016/0009-2509(90)87059-2.
Pham, H.N., & Doherty, M.F. (1990b). Design and synthesis of heterogeneous azeotropic distillations—III. Column sequences. Chemical Engineering Science 45(7), 1845-1854. DOI: 10.1016/0009-2509(90)87060-6.
Pham, H.N., Ryan, P.J., & Doherty, M.F. (1989). Design and minimum reflux for heterogeneous azeotropic distillation columns. AICHE Journal 35(10), 1585-1591.
DOI: 10.1002/aic.690351002.
Prayoonyong, P., & Jobson, M. (2011). Flowsheet synthesis and complex distillation column design for separating ternary heter-ogeneous azeotropic mixtures. Chemical Engineering Research and Design 89(8), 1362-1376.
DOI: 10.1016/j.cherd.2011.02.015.
Renon, H., & Prausnitz, J.M. (1968). Local compositions in thermo-dynamic excess functions for liquid mixtures. AICHE Journal 14(1), 135-144.
DOI: 10.1002/aic.690140124.
Sánchez, C.A., Estupiñan, L., & Salazar, M.A. (2010). Herramientas para la caracterización termodinámica de sistemas ternarios en destilación. (Spanish). Revista EIA (13), 77-91.
Sánchez, C.A., Gómez, M.Á., & Rodríguez, G. (2013). Caracterización termodinámica para sistemas de esterificación heterogéneos en destilación reactiva. I. Envolventes reactivas. (Spanish), Revista EIA 10(20), 73-85.
Sebastiani, E., & Lacquaniti, L. (1967). Acetic acid—water system thermodynamical correlation of vapor—liquid equilibrium data. Chemical Engineering Science 22(9), 1155-1162. DOI: 10.1016/0009-2509(67)80182-9.
Taylor, R. (2007). (Di)Still Modeling after All These Years: A View of the State of the Art. Industrial & Engineering Chemistry Research 46(13), 4349-4357.
DOI: 10.1021/ie061626m.
Urdaneta, R.Y., Bausa, J., Bruggemann, S., & Marquardt, W. (2002). Analysis and conceptual design of ternary heterogeneous azeotropic distillation processes. Industrial & Engineering Chemistry Research 41(16), 3849-3866.
DOI: 10.1021/ie0107486.
Van Dongen, D.B., Doherty, M.F. (1985). Design and synthesis of homogeneous azeotropic distillations. 1. Problem formulation for a single column. Industrial & Engineering Chemistry Fundamentals 24(4), 454-463.
DOI: 10.1021/i100020a010.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2015 Carlos Arturo Martinez Riascos, Libardo Estupiñan Perez

Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Los autores o titulares del derecho de autor de cada artículo confieren a la revista Ingeniería e Investigación de la Universidad Nacional de Colombia una autorización no exclusiva, limitada y gratuita sobre el artículo que una vez evaluado y aprobado se envía para su posterior publicación ajustándose a las siguientes características:
1. Se remite la versión corregida de acuerdo con las sugerencias de los evaluadores y se aclara que el artículo mencionado se trata de un documento inédito sobre el que se tienen los derechos que se autorizan y se asume total responsabilidad por el contenido de su obra ante la revista Ingeniería e Investigación, la Universidad Nacional de Colombia y ante terceros.
2. La autorización conferida a la revista estará vigente a partir de la fecha en que se incluye en el volumen y número respectivo de la revista Ingeniería e Investigación en el Sistema Open Journal Systems y en la página principal de la revista (https://revistas.unal.edu.co/index.php/ingeinv), así como en las diferentes bases e índices de datos en que se encuentra indexada la publicación.
3. Los autores autorizan a la revista Ingeniería e Investigación de la Universidad Nacional de Colombia para publicar el documento en el formato en que sea requerido (impreso, digital, electrónico o cualquier otro conocido o por conocer) y autorizan a la revista Ingeniería e Investigación para incluir la obra en los índices y buscadores que estimen necesarios para promover su difusión.
4. Los autores aceptan que la autorización se hace a título gratuito, por lo tanto renuncian a recibir emolumento alguno por la publicación, distribución, comunicación pública y cualquier otro uso que se haga en los términos de la presente autorización.


























