Entrepreneurship and Decision- Making in Latin America
Emprendimiento y toma de decisiones en Latinoamérica
Empreendedorismo e tomada de decisões na América Latina
DOI:
https://doi.org/10.15446/innovar.v24n1spe.47557Palabras clave:
Entrepreneurship, Latin America, decision making, investment selection, aggregation operators, probabilities (en)emprendimiento, Latinoamérica, toma de decisiones, selección de inversiones, operadores de agregación, probabilidade (es)
Empreendedorismo, América Latina, tomada de decisões, escolha de investimentos, operadores de agregação, probabilidades (pt)
El objetivo principal de este artículo es analizar diferentes métodos de toma de decisiones, con enfoque en el emprendimiento en Latinoamérica. Los métodos de toma de decisiones pueden recibir información por parte de operadores de agregación basados en el uso de probabilidades, promedios ponderados (PP) y operadores de agregación generalizados. El artículo presenta un nuevo operador probabilístico generalizado de promedios ponderados (GPWA) que unifica los promedios ponderados y la probabilidad en la misma formulación, considerando el grado de importancia de cada concepto usado en el análisis. La ventaja fundamental de este enfoque es que incluye un amplio rango de casos particulares, incluyendo el operador probabilístico de promedios ponderados, el operador probabilístico de promedios geométricos ponderados y el operador probabilístico de promedios cuadráticos ponderados. Se emplean medios cuasiaritméticos para obtener el operador cuasiprobabilístico de promedios ponderados y para generalizar el enfoque, que luego es aplicado a un conjunto de decisiones empresariales hipotéticas en cuanto a inversión en una región latinoamericana unificada políticamente.
Entrepreneurship and Decision- Making in Latin America1
Emprendimiento y toma de decisiones en Latinoamérica
Entrepreneuriat et prise de décisions en Amérique latine
Empreendedorismo e tomada de decisões na América Latina
José M. MerigóI, Marta Peris-OrtizII
I PhD in Business. Researcher. University of Manchester. Manchester Business School. Booth Street West, M15 6PB, Manchester, UK. E-mail: jose.merigolindahl@mbs.ac.uk
II PhD in Business. Associate Professor. Department of Business Organization, Universitat Politècnica de València. Camino Vera s/n, 46022 Valencia, Spain. Email: mperis@doe.upv.es
Correspondencia: Marta Peris-Ortiz. PhD in Business. Associate Professor. Department of Business Organization, Universitat Politécnica de Valência. Camino Vera s/n, 46022 Valencia, Spain. Email: mperis@doe.upv.es.
Citación: Merigó, J. M., & Peris-Ortiz, M. (2014). Entrepreneurship and Decision-Making in Latin America. Innovar, vol. 24, Edición Especial 2014, 101-111.
Clasificación JEL: C44, C49, D81, D89.
Recibido: Agosto de 2012, Aprobado: Enero de 2014.
Abstract:
The principal purpose of this paper is to analyze different methods for decision making, with a focus on entrepreneurship in Latin America. Decision-making methods may be informed by aggregation operators that are based on the use of probabilities, weighted averages (WAs) and generalized aggregation operators. The paper presents a new generalized probabilistic weighted averaging (GPWA) operator that unifies WAs and probability in the same formulation, considering the degree of importance of each concept used in the analysis. The fundamental advantage of this approach is that it includes a wide range of particular cases including the probabilistic weighted averaging (PWA) operator, the probabilistic weighted geometric averaging (PWGA) operator and the probabilistic weighted quadratic averaging (PWQA) operator. Quasi-arithmetic means are used to obtain the Quasi-PWA operator and to generalize the approach, which is then applied to a set of hypothetical entrepreneurial investment decisions in a politically unified Latin American region.
Key words: Entrepreneurship, Latin America, decision making, investment selection, aggregation operators, probabilities, investment selection.
Resumen:
El objetivo principal de este artículo es analizar diferentes métodos de toma de decisiones, con enfoque en el emprendimiento en Latinoamérica. Los métodos de toma de decisiones pueden recibir información por parte de operadores de agregación basados en el uso de probabilidades, promedios ponderados (PP) y operadores de agregación generalizados. El artículo presenta un nuevo operador probabilístico generalizado de promedios ponderados (GPWA) que unifica los promedios ponderados y la probabilidad en la misma formulación, considerando el grado de importancia de cada concepto usado en el análisis. La ventaja fundamental de este enfoque es que incluye un amplio rango de casos particulares, incluyendo el operador probabilístico de promedios ponderados, el operador probabilístico de promedios geométricos ponderados y el operador probabilístico de promedios cuadráticos ponderados. Se emplean medios cuasiaritméticos para obtener el operador cuasiprobabilístico de promedios ponderados y para generalizar el enfoque, que luego es aplicado a un conjunto de decisiones empresariales hipotéticas en cuanto a inversión en una región latinoamericana unificada políticamente.
Palabras clave: emprendimiento, Latinoamérica, toma de decisiones, selección de inversiones, operadores de agregación, probabilidades.
Résumé:
L'objectif principal de cet article consiste à analyser diverses méthodes pour prendre des décisions du point de vue de l'entrepreneu-riat en Amérique latine. Ces méthodes peuvent recevoir une information d'opérateurs d'agrégation basés sur l'utilisation de probabilités, moyennes pondérées (Mp) et opérateurs d'agrégation généralisés. L'article présente un nouvel opérateur de probabilités généralisé de moyennes pondérées (GPWA) qui unifie les moyennes pondérées et la probabilité dans une même formulation, considérant le degré d'importance de chacun des concepts utilisés dans l'analyse. L'avantage fondamental de cette approche consiste en ce qu'elle inclut un vaste éventail de cas particuliers: l'opérateur probabiliste de moyennes pondérées, le probabiliste de moyennes géométriques pondérées et le probabiliste de moyennes quadratiques pondérées. Des moyens quasi-arithmétiques sont utilisés pour obtenir l'opérateur quasi-probabiliste de moyennes pondérées et pour gé-néraliser l'approche qui, ensuite, est appliquée à un ensemble de décisions entrepreneuriales hypothétiques à propos de l'investissement dans une région latino-américaine unifiée politiquement.
Mots-clés: Entrepreneuriat, Amérique Latine, prise de décisions, sélection des investissements, opérateurs d'agrégation, probabilités.
Resumo:
O objetivo principal deste artigo é o de analisar diferentes métodos para tomar decisões, com enfoque no empreendedorismo na América Latina. Esses métodos podem receber informação de operadores de agregação apoiados no uso de probabilidades, médias ponderadas (MP) e operadores de agregação generalizados. O artigo apresenta um novo operador probabilístico generalizado de médias ponderadas (GMWA) que unifica as médias ponderadas e a probabilidade na mesma formulação, considerando o grau de importância de cada conceito utilizado na análise. A vantagem fundamental desta visão é que inclui uma ampla faixa de casos particulares: O operador probabilístico de médias ponderadas, o probabilístico de médias geométricas ponderadas e o probabilístico de médias quadráticas ponderadas. São utilizadas médias quasearitméticas para obter o operador quaseprobabilístico de médias ponderadas e para generalizar a visão e, depois é aplicado a um conjunto de decisões empresariais hipotéticas quanto a investimento em uma região latino-americana unificada politicamente.
Palavras-chave: Empreendedorismo, América Latina, tomada de decisões, escolha de investimentos, operadores de agregação, probabilidades.
Introduction
Theories of decision-making are very popular in the literature because they affect a wide range of fields including economics, computer science, psychology and business administration (Figueira, Greco & Ehrgott, 2005; Gil-Aluja, 1998; Torra & Narukawa, 2007; Zavadskas & Turskis, 2011). Decision problems can be addressed using a variety of tools that enable optimal decisions to be made. A frequently-used tool is the aggregation operator (Beliakov, Pradera & Calvo, 2007; Calvo, Mayor & Mesiar, 2002; Merigó & Yager, 2013; Yager & Kacprzyk, 1997; Yager, Kacprzyk & Beliakov, 2011), of which weighted average (WA) is one of the most commonly used in the literature. Another interesting aggregation operator is probability. These two concepts have been used in economics, engineering and physics and are probably the most relevant for the field of statistics. There are, however, many other aggregation operators, such as the ordered weighted averaging (OWA) operator and others (Belles, Sampera, Merigó, Guillén & Santolino, 2013; Fodor, Marichal & Roubens, 1995; Xu & Da, 2003; Yager, 1988, 1993, 2004; Yager & Kacprzyk, 1997). A particularly interesting type of generalization can be obtained by using generalized and quasi-arithmetic means to provide the generalized weighted average (GWA) and the generalized probabilistic aggregation operator.
Recently, Merigó has suggested a new model, called the probabilistic weighted averaging (PWA) operator, which unifies weighted average with probability (Merigó, 2012a). The main advantage of the PWA is that it is able to unify probability and WA in the same formulation and consider the degree of importance of each concept in the aggregation.
This paper presents a new approach that unifies weighted average and probability in the same formulation; it is capable of considering the importance of each concept in the aggregation within a broader framework of generalized and quasi-arithmetic means. Thus, we present two new general aggregation operators, the generalized PWA (GPWA) and the quasi-arithmetic PWA (Quasi-PWA) operator. Their main advantage over the PWA is that they are more robust and general, as they include the PWA as a particular case as well as many other particular cases not included in the PWA. For example, they include the geometric PWA (PWGA) operator, the quadratic PWA (PWQA) operator, the harmonic PWA (PWHA) operator, generalized probability and the GWA. We also examine some of the principal properties of the GPWA operator.
Applicability of the GPWA is extremely broad, because any study that uses WA or probability may be revised and extended using the new approach, which is therefore very useful in the fields of statistics, economics, engineering, and decision theory. In this research the GPWA is tested using a range of hypothetical Latin American decision-making problems, with a focus on entrepreneurship. The problems range from global to individual country-level issues in law, politics, economics and science; they are important decisions because they involve large sums of money. It is therefore useful to use group decision-making techniques in order to assess the information more comprehensively and, thereby, reach optimal decisions and maximize benefits. This is the framework chosen to present the multi-person GPWA (MP-GPWA) operator.
The paper is justified by the contribution these techniques make to decision-making, and their role as enablers for the entrepreneurial field, especially for complex and broad decision processes that occur within a decision-making group. These techniques may be appropriate for adopting decisions that affect broad economic areas where different experts intervene or for deciding, in an entrepreneurial context, on investment projects where it is advisable to count with opinions from different experts. This approach facilitates the discovery of opportunities (Shane & Venkataraman, 2000; Shane 2012), investment decisions and the corresponding creation of new companies (Audretsch & Thurik, 2001; Parker & Praag, 2012; Wennekers & Thurik, 1999), or the extension of existing investments to give rise to new combinations of factors and innovation (Barney & Wright, 1998; Hayton, 2005; Schumpeter, 1934).
In this context of different dimensions of entrepreneurship, the relation between entrepreneurial activities and company creation is fundamentally important in three ways: for innovation, as mentioned above, because company creation facilitates new combinations of factors (Hisrich & Peters, 1989; Schumpeter, 1934); for regional development and competitive advantages in relation to other countries and regions (Dubini, 1989; Porter, 1990; Reynolds, Bygrave, Autio, Cox & Hay, 2002, 2003); and for resolving the issue of unemployment (Storey, 1982; White & Reynolds, 1996), which is a particularly important problem in Latin America.
In order to contribute to promoting entrepreneurship in these three ways and, consequently, to facilitating regional development, this article provides techniques for decision-making. The originality of the work lies in the proposed set of algorithms that can be used when making political or investment decisions that require the input of groups of experts.
SMEs should also find the algorithms presented here useful when they come to consult experts (Blackburn & Kovalainen, 2009). They should also prove useful for investment and growth decisions (Baum, Locke & Smith, 2001) taken by any company that consults different experts on the advisability of an investment. According to Schumpeter (1934, pp. 6668), entrepreneurs make new combinations of factors "and the new combinations appear discontinuously". Their actions involve innovation and economic developments which can be carried out by "the same people who control the productive or commercial process (in the enterprise)" or by "the new (innovator people)", who generally, in a fresh venture, achieve new combinations or innovations. This widely accepted characterization of entrepreneurship, however, ignores the decisive step of the investment decision and the criteria and techniques that enable its adoption, wherein lies the contribution of this work.
The fact that the entrepreneurship literature has emphasized personal characteristics and intuition as the sources of new initiatives and discovery of opportunities (Cuervo, 2005), makes this contribution towards identifying techniques on which to base decisions even more necessary. Entrepreneurial decision-making and its fields of action, which involve creating and building and enterprises and developing economies and societies in large areas (Europe or Latin America) depends, to some extent, on procedures (or algorithms) such as the ones proposed here if the complexity of the choices to be made are to be understood and the appropriate decisions taken in each case.

A group decision-making problem concerning the selection of investments is used to illustrate this new approach. In the example, a decision-maker has some resources available for creating a new company in the industrial sector and has to decide which Latin American country to invest in. In risky and uncertain environments results may lead to different decisions depending on the importance attached to probability and the WA.
This paper is organized as follows. In Section 2, we briefly review some basic concepts regarding weighted aggregation operators, probabilistic aggregation operators and generalized aggregation operators. Section 3 presents the GPWA operator and the Quasi-PWA operator. Section 4 analyzes some important real cases and Section 5 analyses the applicability of the approach for group decision-making problems with a particular focus on entrepreneurial problems in Latin America. Section 6 presents an illustrative example of the new approach and Section 7 summarizes the main results of the paper.
Aggregation Operators
In this Section, we briefly describe the weighted, probabilistic and generalized aggregation functions and the PWA operator.
Weighted Aggregation Functions
Weighted aggregation functions are functions that weight the aggregation process using the weighted average. The weighted average can be defined as follows:
A WA operator of dimension n is a mapping WA: Rn → R that has an associated weighting vector W, with wi ε [0, 1] and  , such that:
, such that:
where ai represents the ith argument variable.
Other extensions of the weighted average are those that use it with the OWA operator such as the weighted ordered weighted average (WOWA) operator (Torra, 1997; Torra & Narukawa, 2007) and the hybrid averaging (HA) operator (Wei, Zhao & Lin, 2013; Xu & Da, 2003). Recently, Merigó (2011) suggested another approach called the OWA weighted average (OWAWA) operator whose principal advantage compared to the WOWA and the HA is that it includes the OWA and the WA and considers the degree of importance of each in the aggregation. It may be defined as follows.
An OWAWA operator of dimension n is a mapping OWAWA: Rn→ R that has an associated weighting vector W of dimension n such that wj e [0, 1] and  , according to the following formula:
, according to the following formula:
where bj is the jth largest of the ai, each argument aihas an associated weight (WA) viwith 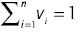 and v ε [0, 1],
and v ε [0, 1],  with ß ε [0, 1] and vjis the weight (WA) v ordered according to bj, that is, according to the jth largest of the ai.
with ß ε [0, 1] and vjis the weight (WA) v ordered according to bj, that is, according to the jth largest of the ai.
Note that other approaches for unifying the OWA and the WA are possible, as suggested by Merigó (2011) using a similar approach to immediate probability. Thus, in WAs the immediate weighted OWA (IWOWA) operator can be defined, for example, by using either 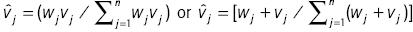 .
.
Note that the literature contains many extensions of weighted aggregation functions, such as those that use uncertain information represented in the form of interval numbers, fuzzy numbers or linguistic variables (Liu, 2013; Merigó, Gil-Lafuente, Zhou & Chen, 2012).
Probabilistic Aggregation Functions
Probabilistic aggregation functions (or operators) are functions that use probabilistic information in the aggregation process. Examples include aggregation with simple probabilities, aggregation with belief structures, the concept of immediate probabilities (Engemann, Filev & Yager, 1996; Yager, Engemann & Filev, 1995) and the probabilistic OWA operator (Merigó, 2012b; Merigó & Wei, 2011). Immediate probability is an approach that uses OWAs and probabilities in the same formulation. It may be defined as follows.
An IPOWA operator of dimension n is a mapping IPOWA: Rn → R that has an associated weighting vector W of dimension n such that Wj e [0, 1] and 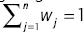 , according to the following formula:
, according to the following formula:

where bj is the jth largest of the ai, each argument ai has a probability viwith 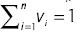 and vi ε [0, 1],
and vi ε [0, 1], 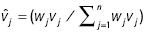 and vjis the probability viordered according to bj, that is, according to the jth largest of the ai .
and vjis the probability viordered according to bj, that is, according to the jth largest of the ai .
Note that the IPOWA operator is a good approach for unifying probabilities and OWAs in certain specific situations. It is not, however, always useful, especially in situations where probabilities or OWA operators need to be given more importance. In order to see why this unification does not appear to constitute a final model, consider other ways of representing vj. For example, it would be possible to consider  or to use other similar approaches.
or to use other similar approaches.
Another approach to unifying probabilities and OWAs in the same formulation is the probabilistic OWA (POWA) operator (Merigó, 2012a), whose main advantage is that it is able to include both concepts, considering the degree of importance of each case in the problem. It may be defined as follows:
A POWA operator of dimension n is a mapping POWA: Rn → R that has an associated weighting vector W of dimension n such that wj e [0, 1] and  , according to the following formula:
, according to the following formula:
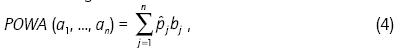
where bj is the jth largest of the ai, each argument a, has an associated probability pi with  and pi ε
and pi ε  with ß ε [0, 1] and pjis the probability piordered according to the jth largest of the ai.
with ß ε [0, 1] and pjis the probability piordered according to the jth largest of the ai.
PWA Operator
The probabilistic weighted averaging (PWA) operator is an aggregation operator that unifies probability and weighted average in the same formulation, considering the degree of importance of each concept in the aggregation. It is defined as follows.
A PWA operator of dimension n is a mapping PWA: Rn → R such that:

where the ai are the argument variables, each argument ai has an associated weight (WA) vi with 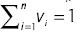 and vi ε [0, 1], and a probabilistic weight pi with
and vi ε [0, 1], and a probabilistic weight pi with  pi, ε [0, 1],
pi, ε [0, 1], 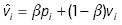 with ß ε [0, 1] and i>, is the weight that unifies probabilities and WAs in the same formulation.
with ß ε [0, 1] and i>, is the weight that unifies probabilities and WAs in the same formulation.
Note that it is also possible to formulate the PWA operator separating the part that strictly affects the probabilistic information from the part that affects the WAs. This representation is useful as it makes it possible to see both models in the same formulation, but it does not seem to be a unique equation that unifies them both. Note that if the weighting vector of probabilities or WAs is not normalized,  the PWA operator can be expressed as:
the PWA operator can be expressed as:

The PWA is monotonic, commutative, bounded and idempotent. For further reading on the PWA, see Merigó (2012a).
Generalized Aggregation Operators
Many aggregation operators use a generalized mean including, among many other possibilities, the weighted generalized mean, the generalized OWA operator and the Minkowski distance. This section provides an example of how to use the generalized mean based on the OWA operator.
The generalized OWA (GOWA) operator was introduced by Yager (2004). It generalizes a wide range of aggregation operators including the OWA operator with its particular cases, the ordered weighted geometric (OWG) operator, the ordered weighted harmonic averaging (OWHA) operator and the ordered weighted quadratic averaging (OWQA) operator. It may be defined as follows.
A GOWA operator of dimension n is a mapping GOWA: Rn → R that has an associated weighting vector W of dimension n with wjß ε [0, 1] and  , such that:
, such that:

where bj is the jth largest of the ai, and λ is a parameter such that λ ε (-∞, ∞) - {0}.
As Yager (2004) has demonstrated, the GOWA operator is a mean operator. This reflects the fact that the operator is commutative, monotonic, bounded and idempotent. It can also be demonstrated that the GOWA operator has as special cases the maximum, the minimum, the generalized mean and the weighted generalized mean. Note that if λ = 1, then OWA operator is used. If λ = 2, then ordered weighted quadratic averaging (OWQA) is the appropriate operator and if λ → 0, then the ordered weighted geometric (OWG) operator is indicated (Zhao, Xu, Ni & Liu , 2010; Zhou & Chen, 2010).
The Generalized Probabilistic Weighted Averaging Operator
The generalized probabilistic weighted averaging (GPWA) operator is an aggregation operator that unifies probability and weighted average in the same formulation, considering the degree of importance of each concept in the aggregation. This approach also uses generalized means to include a wide range of aggregation operators such as the PWA, the probabilistic weighted geometric average (PGWA), the probabilistic weighted harmonic average (PHWA), the probabilistic weighted quadratic average (PQWA), and many others. In this case, the weighted generalized average (WGA) is unified with the probabilistic generalized mean (PGM), and can include other unifications including, for example, the weighted geometric mean (WGM) with the probabilistic geometric mean (PGtM), the weighted quadratic mean (WQM) with the probabilistic quadratic mean (PQM), and so on. It is defined as follows.
A GPWA operator of dimension n is a mapping GPWA: Rn → R such that:

where the ai are the argument variables, each argument ai has an associated weight (PWA) vi with  and vi ε [0, 1], and a probabilistic weight piwith
and vi ε [0, 1], and a probabilistic weight piwith 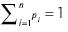 and
and  , is the weight that unifies probabilities and WAs in the same formulation and l is a parameter such that l e (-∞, ∞) - {0}.
, is the weight that unifies probabilities and WAs in the same formulation and l is a parameter such that l e (-∞, ∞) - {0}.
Note that it is also possible to formulate the GPWA operator separating the part that strictly affects probabilistic information and the part that affects the WA. This representation is useful as it makes it possible to see both models in the same formulation, but it does not seem to be a unique equation that unifies both models.
A GPWA operator is a mapping GPWA: Rn→ R of dimension n, if it has an associated probabilistic vector P, with 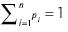 and pi ε [0, 1] and a weighting vector Vthat affects the WA, with
and pi ε [0, 1] and a weighting vector Vthat affects the WA, with  and vi ε [0, 1], such that:
and vi ε [0, 1], such that:

where the aiare the argument variables, ß ε [0, 1] and λ is a parameter such that λ ε (-∞, ∞) - {0}.
Note that if the weighting vector of probabilities or WAs is not normalized, 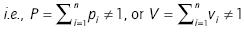 , then, the GPWA operator can be expressed as:
, then, the GPWA operator can be expressed as:

If B is a vector corresponding to the ordered arguments bj, called here the ordered argument vector, and WTis the transpose of the weighting vector, then, the GPWA operator may be expressed as:

The GPWA is monotonic, commutative, bounded and idempotent. It is monotonic because if ai> ui, for all ai, then, GPWA (a1r.., an) > GPWA* (u1 u2.., un). It is commutative because any permutation of the arguments has the same evaluation. It is bounded because the GPWA aggregation is delimited by the minimum and the maximum. That is, Min{ai} < GPWA (a1..., an) < Max{ai}. It is idempotent because if ai= a, for all aa, then, GPWA (a1...,an) = a.
Note that a further generalization of the GPWA operator is possible using quasi-arithmetic means. This generalization is called here the Quasi-PWA operator. It may be defined as follows.
A Quasi-PWA operator of dimension n is a mapping QPWA: Rn→ R that has an associated weighting vector W of dimension n such that the sum of the weights is 1 and wj ε [0, 1], then:

where the ai are the argument variables, each argument aihas an associated weight (PWA) vi with  and vi ε [0, 1], and a probabilistic weight piwith
and vi ε [0, 1], and a probabilistic weight piwith 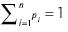 and Pi ε [0, 1], vˆ = ßp, + (1- ß)v, with ß ε [0, 1], v, is the weight that unifies probabilities and WAs in the same formulation and g(b) is a strictly continuous monotone function.
and Pi ε [0, 1], vˆ = ßp, + (1- ß)v, with ß ε [0, 1], v, is the weight that unifies probabilities and WAs in the same formulation and g(b) is a strictly continuous monotone function.
The GPWA operator is generalized using the function g(b). Thus, if g(b) = bλ the Quasi-PWA operator becomes the GPWA operator.
Families of GPWA Operators
First let us consider the two main cases of the PGWA operator that are found by analyzing the coefficient ß. Basically, ß = 0, obtains the weighted generalized mean (WGM) and ß = 1 obtains the generalized probabilistic aggregation (GPA) operator. Note that if vi= 1/n, for all i, then, the generalized mean and the GPA operator (arithmetic generalized probabilistic aggregation (AGPA) operator) are unified. Finally, if pi= 1/n, for all j, then the generalized mean and the GWA operator (the arithmetic generalized weighted average (AGWA) operator) are unified.
Analysis of different values of parameter 1, provides another group of particular cases such as the usual PWA operator, the PWGA operator, the PWQA operator and the PWHA operator.
When λ = 1, the GPWA operator becomes the PWA operator.

Note that, for all ai, pj= 1/n obtains the arithmetic weighted average (AWA) and VI = 1/n, for all ai, obtains the arithmetic probabilistic aggregation (APA) operator.
When λ = 0, the GPWA operator becomes the probabilistic weighted geometric averaging (PWGA) operator.

Note that, for all ai, pj= 1/n obtains the probabilistic geometric arithmetic weighted geometric average (PGAWGA) and vi = 1/n, for all ai, obtains the probabilistic geometric arithmetic mean (PGAM) operator. Note that ß = 1 obtains the probabilistic geometric aggregation (PGA).
λ = -1 obtains the probabilistic weighted harmonic averaging (PWHA) operator.

Note that, for all ai, pj= 1/n obtains the probabilistic harmonic arithmetic weighted harmonic average (PHAWHA) and vi= 1/n, for all ai, obtains the probabilistic harmonic arithmetic mean (PHAM) operator. Note that ß = 1 obtains the probabilistic harmonic aggregation (PHA).
λ = 2 obtains the probabilistic weighted quadratic averaging (PWQA) operator.
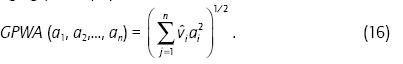
Note that, for all ah pj= 1/n obtains the probabilistic quadratic arithmetic weighted quadratic average (PQAWQA) and vi = 1/n, for all a, obtains the probabilistic quadratic arithmetic mean (PQAM) operator. Note that ß = 1 obtains the probabilistic quadratic aggregation (PQA).
Note that other families could be obtained by using different values in parameter λ, while mixing different classes for each part of the aggregation, for example, could obtain λ = 1 for probabilities and λ = 2 for the WA, thereby obtaining the probabilistic weighted quadratic average (PWQA). Similarly, many other cases such as the probabilistic quadratic weighted geometric average (PQWGA), the probabilistic geometric weighted average (PGWA), the probabilistic geometric weighted quadratic average (PGWQA) could be obtained, and so on.
Decision-Making in Latin America using the GPWA Operator
The GPWA operator may be applied to many problems in decision-making, statistics, engineering and economics. In summary, all the studies that use probability or the weighted average may be revised and extended using this new approach.
This paper focuses on decision-making applications in Latin America, distinguishing between key supranational-and country-level decisions. An interesting issue in this direction is the possible establishment of a new Super State involving most Latin American countries, similar to the European Union (EU), whose creation process would imply multiple key decisions involving millions of dollars. Thus, robust decision-making assessment would be required in order to reach optimal solutions. All aspects have to be considered because decisions are required everywhere including in general supranational policies such as strategic management, innovation and knowledge management. The creation of Latin American supranational law would require many decisions to be made concerning the appropriate regulations required to maximize benefits or minimize costs. The following general areas provide a summary of where new entrepreneurial decisions would have to be taken within the context of Latin American law.
- Constitutional law: The Constitution of a new Super State with fundamental regulations affecting general principles in the region.
- Competition law.
- Tax law.
- Property law.
- Business and banking law.
- Other regulations.
Decision-making is present in all fields since all actions and strategies implicitly involve entrepreneurial decision-making. The following are key areas where decisions are very important for the efficient management of the Latin American region and its constituent countries:
- Politics.
- International relations.
- Monetary, fiscal and commercial policies.
- Other policies.
- Economics.
- Macroeconomics: Decisions concerning the analysis of debt, government spending, taxes, transactions, exports, imports, interest rates, inflation and money supply.
- Microeconomics.
- International economics.
- Development economics.
- Agriculture, manufacturing, service sector and tourism issues.
- Finance.
- The creation and development of a new currency similar to the Euro in the EU.
- National Central Banks and the creation of a Latin American Central Bank with similar characteristics to the European Central Bank.
- A Latin American stock market and other issues concerning Latin American financial integration
- International finance from a Latin American perspective.
- Marketing.
- Management.
- Mathematics and statistics.
- Physics and astronomy.
- Biology and medicine such as regional health service models.
- Sport.
- TV, cinema, radio and newspapers.
In addition a range of other Latin America-wide decision-making scenarios should also be considered, such as:
Usually, because of the large sums involved, such macro decisions are taken by groups of experts rather than a single individual. Thus, group decision-making processes are needed to implement entrepreneurial initiatives. The next section presents a Latin American multi-person decision making problem using the GPWA operator. This provides a method for dealing with the opinions of several experts in a process of analysis, considering the subjective and objective information available in the problem. This aggregation process may be summarized using the following aggregation operator called here the multiperson - GPWA (MP-GPWA) operator.
An MP-GPWA operator of dimension n is a mapping MP-GPWA: Rnx Rp → R that has a weighting vector X of dimension q with 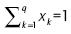 and xk e [0, 1] such that:
and xk e [0, 1] such that:
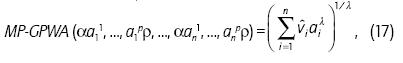
where the aiare the argument variables,  , is the argument variable provided by each person (or expert), each argument ai has an associated weight (PWA) vi with
, is the argument variable provided by each person (or expert), each argument ai has an associated weight (PWA) vi with  and vi ε [0, 1], and a probabilistic weight
and vi ε [0, 1], and a probabilistic weight  with ß ε [0, 1], vi is the weight that unifies probabilities and WAs in the same formulation, and where λ is a parameter such that λ e (- ∞, ∞) - {0}.
with ß ε [0, 1], vi is the weight that unifies probabilities and WAs in the same formulation, and where λ is a parameter such that λ e (- ∞, ∞) - {0}.
The MP-GPWA operator accomplishes similar properties to those explained in Section The Generalized Probabilistic Weighted Averaging Operator. Thus, special cases are:
- The multi-person - arithmetic mean (MP-AM) operator.
- The multi-person - WA (MP-WA) operator.
- The multi-person - PA (MP-PA) operator.
- The multi-person - GWA (MP-GWA) operator.
- The multi-person - GPA (MP-GPA).
Note that more complex situations can be considered by using different types of aggregation operators and many other decision-making methodologies (Antuchevicienè, Za-vadskas & Zakareviclus, 2010; Figueira et aí., 2005; Sonmez & Moorhouse, 2010; Wei, 2010; Xu & Cai, 2012; Yan, 2011; Zavadskas, Kaklauskas, Turskis & Tamosaitiene, 2009; Za-vadskas, Vilutiene, Turskis & Tamosaitiene, 2010; Zhang & Liu, 2010). But this paper focuses on this perspective.
Illustrative Example
Below, we present a brief illustrative example of the new approach applied to a decision-making problem concerning the selection of optimal investments. Consider an entrepreneurial context in which an investor wants to create a new company, has some resources available for the purpose and has to decide where to invest his money. He is considering several countries where the new company might be established but there are several variables that affect the strategy and, depending on the future scenario, the results may be different. Thus, a group of experts is asked to develop a decision-making process to help the entrepreneur ascertain approximately what the expected outcomes are for each alternative.
- A1: Create a new company in Argentina.
- A2: Create a new company in Brazil.
- A3: Create a new company in Colombia.
- A4: Create a new company in Venezuela.
- A5: Do not create any company.
After a careful review of the information, the group of experts establishes the following general information on the alternatives. They assume that profits depend on the future state of nature. In this example, we assume five potential states of nature, S = {S1, S2, S3, S4, S5}:
- S1: Negative growth rate of the economy.
- S2: Growth rate close to 0.
- S3: Low positive growth rate.
- S4: Positive growth rate.
- S5: High growth rate.
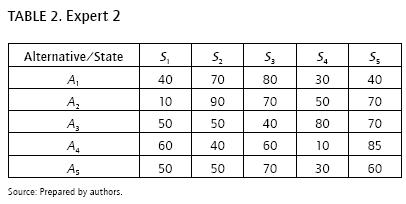
The group of experts is made up of 3 persons, each offering their own single opinion regarding the results obtained by each investment considered. The results are shown in Tables 1, 2 and 3. Note that the results repres ent expected profits between 0 and 100 monetary units.
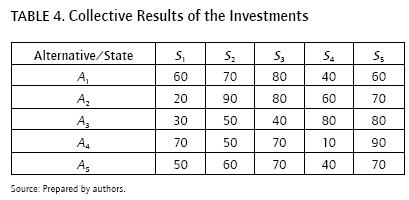
This information can be aggregated in order to make a decision. First, the information of the three groups of experts is aggregated to obtain a collective matrix. The WA obtains this matrix by assuming that the importance of the experts is: X = (0.2, 0.3, 0.5). The results are shown in Table 4.
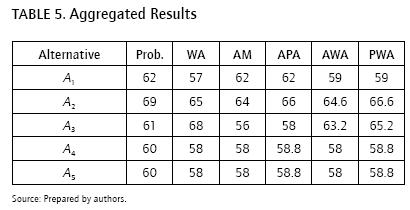
With this information, it is possible to develop different methods based on the GPWA operator for selecting an in -vestment strategy. This example considers probabilistic aggregation, the weighted average, the arithmetic mean, the arithmetic probabilistic aggregation, the weighted arithmetic average and the PWA operator. Assume that ß = 0.4 and the following weights: P = (0.1, 0.2, 0.2, 0.2, 0.3) and V = (0.1, 0.1, 0.1, 0.3, 0.4). The results are shown in Table 5.
As the table shows, depending on the particular type of GPWA operator used, the optimal choice is different. Therefore, it is interesting to establish an ordering of the investment strategies for each particular case. The results are presented in Table 6.
As the table shows each particular type of GPWA operator may lead to a different result and thus the decisions may be different.
Conclusions
The main purpose of this paper was to analyze different methods for decision-making with a focus on entrepre-neurship in Latin America. In this regard it presents a new approach that unifies probability and the weighted average in the same formulation, considering the degree of importance that each concept has in the analysis. This model also uses generalized means, called the generalized probabilistic weighted averaging (GPWA) operator, to provide a more comprehensive formulation of the aggregation operator. The main advantage of this approach is that it includes a wide range of particular cases including, but not confined to, the PWA, the PWGA, the PWQA, the PWHA, the AWA and the APA. The GPWA is further generalized using quasi-arithmetic means, obtaining the Quasi-PWA operator.
Analysis of the applicability of the GPWA operator shows that it is very broad, because all the studies that use probability or the weighted average can be revised and extended using the new approach. Focusing on decision-making problems in Latin America at supranational-and individual country-level, an illustrative example of entre-preneurship was developed, according to which an investor is planning optimal investment in new company creation and has to select the most appropriate Latin American country in which to pursue his strategy. Depending on the particular type of GPWA operator used, the results may differ, although manipulation of the results is not as flexible in this case as with the OWA operator, because it deals with subjective and objective information but does not incorporate the levels of optimism of the decision-maker.
Future research will develop further extensions of this approach, using more general formulations and considering other characteristics of the problem such as the use of uncertain information represented in the form of interval numbers, fuzzy numbers and linguistic variables. The use of distance measures in the analysis and many other applications in decision-making in business and other fields, such as statistics and engineering, will also be considered. In the field of entrepreneurship it will also be interesting to focus on national- and supranational decision-making problems in other regions, because of their relevance and of the large sums of money involved at regional level in Europe, North America, Asia and África, and the particular problems that occur in each individual country.
Pie de página
1Acknowledgements: Support from the University of Barcelona under project 099311 and from the Universitat Politécnica de Valência under project PAID-06-12 (Sp 20120792) is gratefully acknowledged.
References
Antucheviciené, J., Zavadskas, E. K., & Zakarevicius, A. (2010). Multiple criteria construction management decisions considering relations between criteria. Technological and Economic Development of Economy, 16(1), 109-125.
Audretsch, D. B., & Thurik, R. (2001). Linking entrepreneurship to growth. Paris: OECD Directorate for Science, Technology and Industry Working Papers.
Barney, J. B., & Wright, P. M. (1998). On becoming a strategic partner: The role of human resources in gaining competitive advantage. Human Resource Management, 37(1), 31-46.
Baum, J. R., Locke, E. A., & Smith, K. G. (2001). A multidimensional model of venture growth, Academy of Management Journal, 44(2), 292-303.
Beliakov, G., Pradera, A., & Calvo, T. (2007). Aggregation functions: A guide for practitioners. Berlin: Springer-Verlag.
Belles, J., Merigó, J. M., Guillén, M., & Santolino, M. (2013). The connection between distortion risk measures and ordered weighted averaging operators. Insurance: Mathematics and Economics, 52(2), 411-420.
Blackburn, R., & Kovalainen, A. (2009). Researching small firms and en-trepreneurship: Past, present and future, International Journal of Management Reviews, 77(2), 127-148.
Calvo, T., Mayor, G., & Mesiar, R. (2002). Aggregation operators: New trends and applications. New York: Physica-Verlag.
Cuervo, A. (2005). Individual and environmental determinants of en-trepreneurship. International Entrepreneurship and Management Journal, 7, 293-311.
Dubini, P. (1989). The influence of motivations and environment on business start-ups: Some hints for public policies. Journal of Business Venturing, 4(1), 11-26
Engemann, K. J., Filev, D. P., & Yager, R. R. (1996). Modelling decision making using immediate probabilities. International Journal of General Systems, 24(3), 281-294.
Fodor, J., Marichal, J. L., & Roubens, M. (1995). Characterization of the ordered weighted averaging operators. IEEE Transactions on Fuzzy Systems, 3(2), 236-240.
Figueira J., Greco, S., & Ehrgott, M. (2005). Multiple criteria decision analysis: State of the art surveys. Boston: Springer.
Gil-Aluja, J. (1998). The interactive management of human resources in uncertainty. Dordrecht: Kluwer Academic Publishers.
Liu, P. D. (2013). The multi-attribute group decision-making method based on the interval grey linguistic variables weighted aggregation operator. Journal of Intelligent & Fuzzy Systems, 24(2), 405-414.
Hayton, J. C. (2005). Promoting corporate entrepreneurship through human resource management practices: A review of empirical research. Human Resource Management Review, 75, 21-41.
Hisrich, R. D., & Peters, M. (1989). Entrepreneurship: Starting, developing and managing a new enterprise (pp. 3-23). Boston: Richard D. Irwin, Inc.
Merigó, J. M. (2011). A unified model between the weighted average and the induced OWA operator. Expert Systems with Applications, 38(9), 11560-11572.
Merigó, J. M. (2012a). The probabilistic weighted average and its application in multi-person decision making. International Journal of Intelligent Systems, 27(5), 457-476.
Merigó, J. M. (2012b). Probabilities with OWA operators. Expert Systems with Applications, 39(13), 11456-11467.
Merigó, J. M., Gil-Lafuente, A. M., Zhou, L. G., & Chen, H. Y. (2012). Induced and linguistic generalized aggregation operators and their application in linguistic group decision making. Group Decision and Negotiation, 27 (4), 531-549.
Merigó, J. M., & Wei, G. W. (2011). Probabilistic aggregation operators and their application in uncertain multi-person decision making. Technological and Economic Development of Economy, 77(2), 335-351.
Merigó, J. M., & Yager, R. R. (2013). Generalized moving averages, distance measures and OWA operators. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 27(3), 533-559.
Parker, S., & Praag, M. (2012). The entrepreneur's mode of entry: Business takeover or new venture start? Journal of Business Venturing, 27(1), 31-46.
Porter, M. E. (1990). The competitive advantage of nations. New York: Free Press.
Reynolds, P., Bygrave, W. D., Autio, E., Cox, L. W., & Hay, M. (2002). Global Entrepreneurship Monitor. 2002 Executive Report, London: London School Business Eds., Babson College, Kauffman Center for Entrepreneurial Leadership.
Reynolds, P., Bygrave, W. D., Autio, E., et al. (2003). Global Entrepre-neurship Monitor. 2003 Executive Report. London: London School Business Eds., Babson College, Kauffman Center for Entrepreneurial Leadership.
Schumpeter, J. A. (1934). The theory of economic development. Cambridge, MA: Harvard University Press.
Shane, S. (2012). Reflections on the 2010 AMR Decade Award: Delivering on the Promise of Entrepreneurship as a Field of Research. Academy of Management Review, 37(1), 10-20.
Shane, S. & Venkataraman, S. (2000). The promise of entrepreneurship as a field of research. Academy of Management Review, 25(1), 217-226.
Sonmez, M., & Moorhouse, A. (2010). Purchasing professional services: Which decision criteria? Management Decision, 48(2), 189-206.
Storey, J. (1982). Impact on the local economy. In D. J. Storey (Ed.), Entrepreneurship and the new firm (pp. 167-180). London: Croom Helm.
Torra, V. (1997). The weighted OWA operator. International Journal of Intelligent Systems, 72(2), 153-166.
Torra, V., & Narukawa, Y. (2007). Modeling decision: Information fusion and aggregation operators. Berlin: Springer-Verlag.
Wei, G. W. (2010). GRA method for multiple attribute decision making method with incomplete weight information in intuitionistic fuzzy setting. Knowledge-Based Systems, 23(3), 243-247.
Wei, G. W., Zhao, X., & Lin, R. (2013). Some hybrid aggregating operators in linguistic decision making with Dempster-Shafer belief structure. Computers & Industrial Engineering, 65(4), 646-651.
Wennekers, S., & Thurik, R. (1999). Linking entrepreneurship and economic growth. Small Business Economics, 73(1), 27-55.
White, S. B., & Reynolds, P. (1996). Government programs and high growth new firms. Retrieved from http://fusionmx.babson.edu/entrep/fer/papers96/white/.
Xu, Z. S., & Cai, X. (2012). Uncertain power average operators for aggregating interval fuzzy preference relations. Group Decision and Negotiation, 27 (3), 381-397.
Xu, Z. S., & Da, Q. L. (2003). An overview of operators for aggregating the information. International Journal of Intelligent Systems, 78(9), 953-969.
Yager, R. R. (1988). On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Transactions on Systems, Man and Cybernetics, B 78(1), 183-190.
Yager, R. R. (1993). Families of OWA operators. Fuzzy Sets and Systems, 59(2), 125-148.
Yager, R. R. (2004). Generalized OWA aggregation operators. Fuzzy Optimization and Decision Making, 3(1), 93-107.
Yager, R. R., Engemann, K. J., & Filev, D. P. (1995). On the concept of immediate probabilities. International Journal of Intelligent Systems, 70(4), 373-397.
Yager, R. R., & Kacprzyk, J. (1997). The ordered weighted averaging operators: Theory and applications. Norwell, MA: Kluwer Academic Publishers.
Yager, R. R., Kacprzyk, J., & Beliakov, G. (2011). Recent developments in the ordered weighted averaging operators: Theory and practice. Berlin: Springer-Verlag.
Yan, M. R. (2011). A fuzzy logic enhanced bargaining model for business pricing decision support in joint venture projects. Journal of Business Economics and Management, 72(2), 234-247.
Zavadskas, E. K., Kaklauskas, A., Turskis, Z., & Tamosaitiene, J. (2009). Multi-attribute decision-making model by applying grey numbers. Informatica, 20(2), 305-320.
Zavadskas, E. K., & Turskis, Z. (2011). Multiple criteria decision making (MCDM) methods in economics: An overview. Technological and Economic Development of Economy, 77(2), 397-427.
Zavadskas, E. K., Vilutiene, T., Turskis, Z., & Tamosaitiene, J. (2010). Contractor selection for construction works by applying SAW-G and TOPSIS grey techniques. Journal of Business Economics and Management, 77(1), 34-55.
Zhao, H., Xu, Z. S., Ni, M., & Liu, S. (2010). Generalized aggregation operators for intuitionistic fuzzy sets. International Journal of Intelligent Systems, 25(1), 1-30.
Zhang, X., & Liu, P. (2010). Method for aggregating triangular fuzzy intuitionistic fuzzy information and its application to decision making. Technological and Economic Development of Economy, 76(2), 280-290.
Zhou, L. G., & Chen, H. Y. (2010). Generalized ordered weighted logarithm aggregation operators and their applications to group decision making. International Journal of Intelligent Systems, 25(7), 683-707.
Referencias
Antucheviciené, J., Zavadskas, E. K., & Zakarevicius, A. (2010). Multiple criteria construction management decisions considering relations between criteria. Technological and Economic Development of Economy, 16(1), 109-125.
Audretsch, D. B., & Thurik, R. (2001). Linking entrepreneurship to growth. Paris: OECD Directorate for Science, Technology and Industry Working Papers.
Barney, J. B., & Wright, P. M. (1998). On becoming a strategic partner: The role of human resources in gaining competitive advantage. Human Resource Management, 37(1), 31-46.
Baum, J. R., Locke, E. A., & Smith, K. G. (2001). A multidimensional model of venture growth, Academy of Management Journal, 44(2), 292-303.
Beliakov, G., Pradera, A., & Calvo, T. (2007). Aggregation functions: A guide for practitioners. Berlin: Springer-Verlag.
Belles, J., Merigó, J. M., Guillén, M., & Santolino, M. (2013). The connection between distortion risk measures and ordered weighted averaging operators. Insurance: Mathematics and Economics, 52(2), 411-420.
Blackburn, R., & Kovalainen, A. (2009). Researching small firms and en-trepreneurship: Past, present and future, International Journal of Management Reviews, 77(2), 127-148.
Calvo, T., Mayor, G., & Mesiar, R. (2002). Aggregation operators: New trends and applications. New York: Physica-Verlag.
Cuervo, A. (2005). Individual and environmental determinants of en-trepreneurship. International Entrepreneurship and Management Journal, 7, 293-311.
Dubini, P. (1989). The influence of motivations and environment on business start-ups: Some hints for public policies. Journal of Business Venturing, 4(1), 11-26
Engemann, K. J., Filev, D. P., & Yager, R. R. (1996). Modelling decision making using immediate probabilities. International Journal of General Systems, 24(3), 281-294.
Fodor, J., Marichal, J. L., & Roubens, M. (1995). Characterization of the ordered weighted averaging operators. IEEE Transactions on Fuzzy Systems, 3(2), 236-240.
Figueira J., Greco, S., & Ehrgott, M. (2005). Multiple criteria decision analysis: State of the art surveys. Boston: Springer.
Gil-Aluja, J. (1998). The interactive management of human resources in uncertainty. Dordrecht: Kluwer Academic Publishers.
Liu, P. D. (2013). The multi-attribute group decision-making method based on the interval grey linguistic variables weighted aggregation operator. Journal of Intelligent & Fuzzy Systems, 24(2), 405-414.
Hayton, J. C. (2005). Promoting corporate entrepreneurship through human resource management practices: A review of empirical research. Human Resource Management Review, 75, 21-41.
Hisrich, R. D., & Peters, M. (1989). Entrepreneurship: Starting, developing and managing a new enterprise (pp. 3-23). Boston: Richard D. Irwin, Inc.
Merigó, J. M. (2011). A unified model between the weighted average and the induced OWA operator. Expert Systems with Applications, 38(9), 11560-11572.
Merigó, J. M. (2012a). The probabilistic weighted average and its application in multi-person decision making. International Journal of Intelligent Systems, 27(5), 457-476.
Merigó, J. M. (2012b). Probabilities with OWA operators. Expert Systems with Applications, 39(13), 11456-11467.
Merigó, J. M., Gil-Lafuente, A. M., Zhou, L. G., & Chen, H. Y. (2012). Induced and linguistic generalized aggregation operators and their application in linguistic group decision making. Group Decision and Negotiation, 27 (4), 531-549.
Merigó, J. M., & Wei, G. W. (2011). Probabilistic aggregation operators and their application in uncertain multi-person decision making. Technological and Economic Development of Economy, 77(2), 335-351.
Merigó, J. M., & Yager, R. R. (2013). Generalized moving averages, distance measures and OWA operators. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 27(3), 533-559.
Parker, S., & Praag, M. (2012). The entrepreneur's mode of entry: Business takeover or new venture start? Journal of Business Venturing, 27(1), 31-46.
Porter, M. E. (1990). The competitive advantage of nations. New York: Free Press.
Reynolds, P., Bygrave, W. D., Autio, E., Cox, L. W., & Hay, M. (2002). Global Entrepreneurship Monitor. 2002 Executive Report, London: London School Business Eds., Babson College, Kauffman Center for Entrepreneurial Leadership.
Reynolds, P., Bygrave, W. D., Autio, E., et al. (2003). Global Entrepre-neurship Monitor. 2003 Executive Report. London: London School Business Eds., Babson College, Kauffman Center for Entrepreneurial Leadership.
Schumpeter, J. A. (1934). The theory of economic development. Cambridge, MA: Harvard University Press.
Shane, S. (2012). Reflections on the 2010 AMR Decade Award: Delivering on the Promise of Entrepreneurship as a Field of Research. Academy of Management Review, 37(1), 10-20.
Shane, S. & Venkataraman, S. (2000). The promise of entrepreneurship as a field of research. Academy of Management Review, 25(1), 217-226.
Sonmez, M., & Moorhouse, A. (2010). Purchasing professional services: Which decision criteria? Management Decision, 48(2), 189-206.
Storey, J. (1982). Impact on the local economy. In D. J. Storey (Ed.), Entrepreneurship and the new firm (pp. 167-180). London: Croom Helm.
Torra, V. (1997). The weighted OWA operator. International Journal of Intelligent Systems, 72(2), 153-166.
Torra, V., & Narukawa, Y. (2007). Modeling decision: Information fusion and aggregation operators. Berlin: Springer-Verlag.
Wei, G. W. (2010). GRA method for multiple attribute decision making method with incomplete weight information in intuitionistic fuzzy setting. Knowledge-Based Systems, 23(3), 243-247.
Wei, G. W., Zhao, X., & Lin, R. (2013). Some hybrid aggregating operators in linguistic decision making with Dempster-Shafer belief structure. Computers & Industrial Engineering, 65(4), 646-651.
Wennekers, S., & Thurik, R. (1999). Linking entrepreneurship and economic growth. Small Business Economics, 73(1), 27-55.
White, S. B., & Reynolds, P. (1996). Government programs and high growth new firms. Retrieved from http://fusionmx.babson.edu/entrep/fer/papers96/white/.
Xu, Z. S., & Cai, X. (2012). Uncertain power average operators for aggregating interval fuzzy preference relations. Group Decision and Negotiation, 27 (3), 381-397.
Xu, Z. S., & Da, Q. L. (2003). An overview of operators for aggregating the information. International Journal of Intelligent Systems, 78(9), 953-969.
Yager, R. R. (1988). On ordered weighted averaging aggregation operators in multi-criteria decision making. IEEE Transactions on Systems, Man and Cybernetics, B 78(1), 183-190.
Yager, R. R. (1993). Families of OWA operators. Fuzzy Sets and Systems, 59(2), 125-148.
Yager, R. R. (2004). Generalized OWA aggregation operators. Fuzzy Optimization and Decision Making, 3(1), 93-107.
Yager, R. R., Engemann, K. J., & Filev, D. P. (1995). On the concept of immediate probabilities. International Journal of Intelligent Systems, 70(4), 373-397.
Yager, R. R., & Kacprzyk, J. (1997). The ordered weighted averaging operators: Theory and applications. Norwell, MA: Kluwer Academic Publishers.
Yager, R. R., Kacprzyk, J., & Beliakov, G. (2011). Recent developments in the ordered weighted averaging operators: Theory and practice. Berlin: Springer-Verlag.
Yan, M. R. (2011). A fuzzy logic enhanced bargaining model for business pricing decision support in joint venture projects. Journal of Business Economics and Management, 72(2), 234-247.
Zavadskas, E. K., Kaklauskas, A., Turskis, Z., & Tamosaitiene, J. (2009). Multi-attribute decision-making model by applying grey numbers. Informatica, 20(2), 305-320.
Zavadskas, E. K., & Turskis, Z. (2011). Multiple criteria decision making (MCDM) methods in economics: An overview. Technological and Economic Development of Economy, 77(2), 397-427.
Zavadskas, E. K., Vilutiene, T., Turskis, Z., & Tamosaitiene, J. (2010). Contractor selection for construction works by applying SAW-G and TOPSIS grey techniques. Journal of Business Economics and Management, 77(1), 34-55.
Zhao, H., Xu, Z. S., Ni, M., & Liu, S. (2010). Generalized aggregation operators for intuitionistic fuzzy sets. International Journal of Intelligent Systems, 25(1), 1-30.
Zhang, X., & Liu, P. (2010). Method for aggregating triangular fuzzy intuitionistic fuzzy information and its application to decision making. Technological and Economic Development of Economy, 76(2), 280-290.
Zhou, L. G., & Chen, H. Y. (2010). Generalized ordered weighted logarithm aggregation operators and their applications to group decision making. International Journal of Intelligent Systems, 25(7), 683-707.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Julio Albeiro Londoño-Patiño. (2020). Toma de decisiones basada en la productividad en Pymes manufactureras: aproximación desde la Lógica Difusa. Revista CEA, 6(12), p.181. https://doi.org/10.22430/24223182.1507.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2014 Innovar

Esta obra está bajo una licencia internacional Creative Commons Reconocimiento-NoComercial-CompartirIgual 3.0.
Todos los artículos publicados por Innovar se encuentran disponibles globalmente con acceso abierto y licenciados bajo los términos de Creative Commons Atribución-No_Comercial-Sin_Derivadas 4.0 Internacional (CC BY-NC-ND 4.0).
Una vez seleccionados los artículos para un número, y antes de iniciar la etapa de cuidado y producción editorial, los autores deben firmar una cesión de derechos patrimoniales de su obra. Innovar se ciñe a las normas colombianas en materia de derechos de autor.
El material de esta revista puede ser reproducido o citado con carácter académico, citando la fuente.
Esta obra está bajo una Licencia Creative Commons: