Sum of squares decomposition: theory and applications in control
Descomposición en suma de cuadrados: teoría y aplicaciones en control
DOI:
https://doi.org/10.15446/ing.investig.v30n3.18178Keywords:
sum of squares (SOS), stability analysis, nonlinear systems, switched systems (en)suma de cuadrados, SOS, análisis de estabalidad, sistemas no lineales, sistemas conmutados (es)
Downloads
The sum of squares (SOS) decomposition technique allows numerical methods such as semidefinite programming to be used for proving the positivity of multivariable polynomial functions. It is well known that it is not an easy task to find Lyapunov functions for stability analysis of nonlinear systems. An algorithmic tool is used in this work for solving this problem. This approach is presented as SOS programming and solutions were obtained with a Matlab toolbox. Simple examples of SOS concepts, stability analysis for nonlinear polynomial and rational systems with uncertainties in parameters are presented to show the use of this tool. Besides these approaches, an alternative stability analysis for switched systems using a polynomial approach is also presented.
Las técnicas de descomposición en sumas de cuadrados (SOS) permiten emplear métodos numéricos para probar la positividad de funciones polinómicas multivariables resolviendo problemas de programación en semidefinida. Teniendo en cuenta que generalmente es difícil encontrar funciones de Lyapunov para realizar análisis de estabilidad en sistemas no lineales, con el uso de técnicas SOS se utiliza una herramienta computacional para resolver este problema, planteando las condiciones de estabilidad como un problema SOS y obteniendo la solución con un toolbox de Matlab. Para mostrar el uso de esta herramienta se presentan ejemplos simples de los conceptos de SOS, análisis de estabilidad para sistemas no lineales polinomios, racionales, con incertidumbre en los parámetros y de sistemas conmutados con una aproximación en polinomio. Con dicha aproximación se encuentran funciones adecuadas para demostrar estabilidad asintótica para estos sistemas.
Andrés Pantoja1 , Eduardo Mojica Nava2 y Nicanor Quijano3
1 Ingeniero Electrónico, Universidad Nacional de Colombia Sede Manizales. M.Sc., en Ingeniería Electrónica, Universidad de los Andes. Estudiante de Doctorado, Universidad de los Andes. Universidad de Nariño, Pasto. ad.pantoja24@uniandes.edu.co.
2 Ingeniero Electrónico, Universidad Industrial de Santander. M.Sc., en Ingeniería Electrónica, Universidad de los Andes. Ph.D., en Ingeniería, Universidad de los Andes y Ecole Centrale Nantes, Francia. Universidad Católica, Bogotá, Colombia. ea.mojica70@uniandes.edu.co.
3 Ingeniero Electrónico, Pontificia Universidad Javeriana, Bogotá, Colombia. M.Sc., and Ph.D., en Ingenieria Electronica, Ohio State University, Columbus, OH, USA. Universidad de los Andes, Bogotá, Colombia. nquijano@uniandes.edu.co
RESUMEN
Las técnicas de descomposición en sumas de cuadrados (SOS) permiten emplear métodos numéricos para probar la positividad de funciones polinómicas multivariables resolviendo problemas de programación en semidefinida. Teniendo en cuenta que generalmente es difícil encontrar funciones de Lyapunov para realizar análisis de estabilidad en sistemas no lineales, con el uso de t técnicas SOS se utiliza una herramienta computacional para resolver este problema, planteando las condiciones de estabilidad como un problema SOS y obteniendo la solución con un toolbox de Matlab. Para mostrar el uso de esta herramienta se presentan ejemplos simples de los conceptos de SOS, análisis de estabilidad para sistemas no lineales polinomios, racionales, con incertidumbre en los parámetros y de sistemas conmutados con una aproximación en polinomio. Con dicha aproximación se encuentran funciones adecuadas para demostrar estabilidad asintótica para estos sistemas.
Palabras claves: suma de cuadrados, SOS, análisis de estabilidad, sistemas no lineales, sistemas conmutados.
ABSTRACT
Sum of squares decomposition (SOS) techniques allow us to use numerical methods, such as semidefinite programming, to prove positivity of multivariable polynomial functions. It is well known that it is not an easy task to find Lyapunov functions for stability analysis of nonlinear systems. In this work, we use an algorithmic tool to solve this problem. This approach is presented as SOS programming and solutions are obtained with a Matlab toolbox. We present simple examples of SOS concepts, stability analysis for nonlinear polynomial, and rational systems with uncertainties in the parameters to show the use of this tool. Besides of these approaches, we present an alternative stability analysis for switched systems with a polynomial approach.
Keywords: sum of squares, SOS, stability analysis, nonlinear systems, switched systems.
Recibido: abril 30 de 2009
Aceptado: noviembre 15 de
2010
Introducción
La teoría sobre la descomposición de funciones poligonales en sumas de cuadrados (SOS) ha tenido un desarrollo importante en los últimos diez años desde su introducción en (Parrilo, 2000). Este impulso se debe principalmente a la posibilidad de realizar relajaciones de problemas considerados NP-hard (e. g., la evaluación de la no negatividad de polinomios multivariables) (Papadimitriou, 1994), a problemas solucionables computacionalmente en tiempo polinomio. El problema consiste básicamente en encontrar condiciones para verificar la validez de la proposición
Para considerar el estudio algorítmico de este problema es evidente la necesidad de delimitar la estructura de las posibles funciones F, y al mismo tiempo hacer el problema lo suficientemente general para garantizar la aplicabilidad de los resultados. Un buen compromiso es alcanzado restringiendo la clase de F a funciones poligonales (Parrilo, 2000).
F(x1,...,xn)≥0, ∀x1,...,xn∈Rn (1)Definición 1.1.Una función f polinomio en x1, . . . , xn, con coeficientes en un campo k, es una combinación lineal finita de monomios:
f= ∑αcαxα=∑αcαx1α1...xnαn cα>k (2)
donde la suma es sobre un número finito de n−tuplas
α = (α1, ..., αn), con αi∈ N0.
Es posible mostrar que el problema general de probar positividad global de una función en polinomio es también de hecho NP-hard (cuando el grado es al menos cuatro). Así que, cualquier método para garantizar la solución del problema en cada caso posible tendrá un comportamiento inaceptable en tiempo computacional para una función con un número de variables elevado.
Ésta es la principal desventaja de las metodologías teóricas tales como eliminación de cuantificadores (Parrilo, 2000).
Si se desean evitar los problemas de complejidad inherentes relacionados con la solución exacta, surge la siguiente cuestión: ¿hay algunas condiciones, que puedan ser probadas en tiempo polinomio para garantizar positividad global de una función? Como se verá en la siguiente sección, tal condición está dada por la existencia de una descomposición en suma de cuadrados.
Entre los problemas que pueden ser tratados por medio de las técnicas de SOS se encuentran optimizaciones globales, con restricciones y booleanas (Prajna et al., 2004), así como problemas aplicados al control como la búsqueda de funciones de Lyapunov para comprobación de estabilidad de puntos de equilibrio en sistemas no lineales (Topcu et al., 2008) y la delimitación de la incertidumbre en los parámetros en el análisis de sistemas dinámicos (Topcu y Packard, 2009). Además se ha explorado el análisis de estabilidad de sistemas no lineales con retardos de tiempo (Papachristodoulou, 2004) y la síntesis de controladores no lineales (Franze et al., 2009; Ebenbauer y Allg¨ower, 2006).
Específicamente, las técnicas SOS plantean un problema de optimización convexa que puede ser resuelto mediante programación semidefinida (SDP) (Parrilo, 2003). Este método es una generalización en la programación lineal (LP), donde las restricciones de no negatividad de las variables son reemplazadas por desigualdades matriciales semidefinidas positivas. La resolución de SDP se realiza con base en técnicas algorítmicas como las desigualdades lineales matriciales (LMI) y programas con métodos numéricos para SDP tales como SeDuMi y SPDT3 (Anjos y Burer, 2007).
Luego la resolución de un problema SOS implica la formulación de un problema SDP, encontrar la solución numérica y luego interpretar el resultado de forma que corresponda al problema inicial propuesto. Para el desarrollo de este proceso se utiliza el toolbox denominado SOSTOOLS (Prajna et al.), que brinda herramientas para el planteamiento de variables, funciones y restricciones en forma de SOS para la obtención de soluciones utilizando entorno simbólico de Matlab.
En este tutorial se presentan los conceptos básicos de las técnicas SOS, algunas aplicaciones en control como la determinación de funciones de Lyapunov, el análisis de la variación de los parámetros en sistemas no lineales con campos vectoriales racionales, la aplicación a sistemas conmutados y la utilización de SOS TOOLS en la resolución de los problemas planteados.
Suma de cuadrados
En esta sección se presentan conceptos importantes y ejemplos básicos del uso de SOS para observar la funcionalidad de la descomposición de una función en una suma de cuadrados, estableciendo bases para las aplicaciones en el área de control y partiendo del análisis de funciones poligonales multivariables.
Además, se introduce SOSTOOLS como la herramienta computacional utilizada en la resolución numérica de los problemas planteados como principales aplicaciones de estas técnicas.
Conceptos básicos
Definición 2.1.Un polinomio multivariable p(x) de grado 2d en x ∈ Rn, es una suma de cuadrados (SOS) si existen polinomios fi(x) tales que
p(x)= ∑i=1M f12(x) (3)
La descomposición en SOS puede ser expresada también como en (Parrilo, 2003), si existe una matriz Q ∈ Rn×n semidefinida positiva, tal que
p(x)=Z(x)T QZ(x) (4)
donde Z(x) es un vector de monomios en x de grado menor igual a d. Dado que Q = QT _ 0, puede ser factorizada de la forma Q = HHT , donde H ∈ Rn×r con r = rango de Q. Tomando h1, h2, . . . , hr, como las columnas de H, la ecuación (4) puede ser expresada como
p(x)= ∑i=1 (hT1Z(x))2 (5)
Entonces, el problema de la determinación de la descomposición SOS del polinomio mostrada en la ecuación (5) se puede relajar a encontrar una Q _ 0, convirtiéndose en un problema de programación en semidefinida, como se define en (Parrilo, 2000).
En el siguiente ejemplo se presenta cómo se expresa una función polinomio en forma SOS a través de las formas mostradas en (4) y (5).
Ejemplo 2.1. Encontrar una descomposición en SOS del polinomio dado por
p(x) = 13x41+14x31x2-18x21+14x21x22...
...6x1x2+9x42-30x32x1+9Dado un vector
Z(x) = [1 x22 x1x2 x12]T
se encuentra una matriz QT≥ 0 tal que

Una factorización Q =HHT dada por

da como resultado que
p(x)= (3x12-x1x2-3)2 + (2x21-3x22+5x1x2)2
Es claro que una función SOS es globalmente positiva, pero no todas las funciones positivas son SOS.
Un ejemplo de estas funciones es el llamado polinomio Motzkin, M(x) = x41 x22+x21x42+x63−3x21x22x23. Para demostrar positividad en este tipo de funciones usando técnicas SOS, en (Reznick, 2000) se demuestra que si p(x) > 0, ∀x ∈ Rn, entonces existe un r entero positivo tal que
p(x)(∑ni=1x21)r es SOS
Entonces, el problema se extiende a probar diferentes valores de r hasta encontrar factible la representación SOS del nuevo polinomio.
Herramienta computacional SOSTOOLS
SOSTOOLS (Prajna et al.) es un toolbox de Matlab para la resolución de problemas de suma de cuadrados (SOSP) en combinación con un programa de resolución de problemas de programación semidefinida (e. g., SeDuMi o SDPT3). Esta herramienta permite convertir el SOSP planteado en un problema SDP, utilizar el algoritmo de resolución y expresar la solución en términos de las variables y polinomios iniciales. El procedimiento general para obtener la solución de problemas SOS se resume en:
Definir las restricciones del problema SOS como desigualdades e igualdades en función de las variables definidas anteriormente.
En la siguiente sección se presentan algunas aplicaciones en control, especialmente en el análisis de estabilidad de puntos de equilibrio de sistemas no lineales por medio del método directo de Lyapunov, y en el análisis de estabilidad de sistemas conmutados.
Aplicaciones en control
Como se mencionó, una de las aplicaciones para las técnicas SOS se encuentra en la facilidad computacional de hallar una función de Lyapunov que demuestre la estabilidad de un punto de equilibrio de un sistema no lineal. Esta tarea generalmente resulta difícil, excepto para ciertos sistemas con reducido número de variables y dependiendo de pruebas para funciones conocidas (e. g., funciones de energía) o de métodos específicos (como el del gradiente o Krasovskii), aplicados a campos vectoriales especiales (Khalil, 2002).
En el caso de campos vectoriales y funciones de Lyapunov poligonales las condiciones para verificar la estabilidad del punto de equilibrio, son esencialmente pruebas de no negatividad que pueden resultar en problemas NP-Hard. Cambiando estas condiciones por la búsqueda de funciones SOS el problema puede ser resuelto utilizando la herramienta algorítmica SOSTOOLS.
En los ejemplos siguientes se aplica la herramienta en el análisis de sistemas polinomios, racionales y con incertidumbres en los parámetros, realizando variaciones en los algoritmos simples originales y con base en ampliaciones del teorema fundamental de Lyapunov.
Sistemas con campos vectoriales polinómicos y racionales
El teorema de estabilidad de Lyapunov en forma general se aplica a un sistema autónomo de la forma
x.=f(x) (6)
donde f : D →Rn es un mapeo continuo de D ⊂ Rnen Rn, y sin pérdida de generalidad (Khalil, 2002); el origen es un punto de equilibrio de (6) (i. e., f (0) = 0). Si se define una función en continuamente diferenciable V(x) denominada función de Lyapunov, las condiciones de estabilidad del sistema se RESUMEN en que si V(x) es definida positiva y ˙V (x) es semidefinida negativa, el origen es estable. Si además, ˙V (x) es definida negativa, el origen es asintóticamente estable.
Para aplicar las técnicas SOS es necesario realizar una relajación de las condiciones de este teorema, con el fin de que las condiciones de no negatividad sean expresadas como sumas de cuadrados. En el caso de sistemas polinomios, teniendo un estado x = [x1, x2, . . . , xn], se define una función V(x) de grado 2d y una función auxiliar φ(x) de la forma
φ(x)= ∑i=1n ∑nj=1εijx12j (7)
con e ε ≥ 0, para todo i y j y ∑aj=1εij> 0, para todo i = 1, 2, . . . , n. Con estas condiciones, φ(x) es definida positiva. Por lo tanto, si V(x)−φ(x) puede ser expresado como una suma de cuadrados, se garantiza que V(x) es definida positiva también.
Entonces, las condiciones de estabilidad pueden ser expresadas como
V(x)−φ(x) es SOS (8)
- δV/δx f(x) es SOS (9)
Por lo tanto, el algoritmo para encontrar una función de Lyapunov usando SOSTOOLS se resume en:
Definir una función polinómica general V(x) de grado determinado (2d) con monomios en x de grado d.
Crear
la expresión φ(x) como en (7).
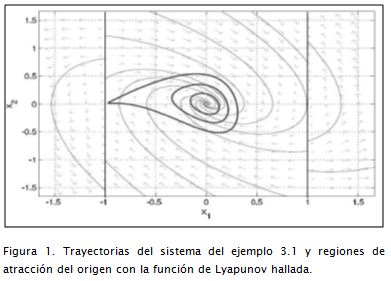
Ejemplo 3.1 (Khalil, 2002). Encontrar una función de Lyapunov que demuestre la
estabilidad asintótica del origen del siguiente sistema: x.1= x2(1-x21) El sistema tiene un punto
de equilibrio en x = 0. Este punto de equilibrio no es único, ya que en x1
= 1 y en x1 = −1, ˙ x1 = 0 y
˙ x2 = 0. Luego al determinar una función de Lyapunov que cumpla
con (8) y (9) se comprueba la estabilidad del origen y se puede establecer una
posible región de atracción observando las curvas de nivel de la función V(x)
encontrada. Usando SOSTOOLS se halla una
función de grado 8, con 42 términos cuyas curvas de nivel se muestran en el
plano de fase del sistema en la Figura 1. Se observa que la mayor región de atracción
para la V(x) encontrada se obtiene al acercarse a x1 = −1,
que es el límite donde las curvas de nivel de la función de Lyapunov dejan de
ser cerradas.
Al tener un sistema con f (x) racional, la condición en (9) se modifica para aplicar el mismo algoritmo en SOSTOOLS.
En este caso se debe encontrar una función
w(x) > 0 tal que
-w(x)- δV/δx f(x) sea SOS y polinómica (11)
Se nota entonces que siendo w(x) > 0, se conserva la segunda condición del teorema general de estabilidad, y siendo (11) una función polinómica, se pueden aplicar nuevamente técnicas SOS para el análisis, como se muestra en el siguiente ejemplo.
Ejemplo 3.2 (Khalil, 2002). Encontrar una función polinómica de Lyapunov para mostrar la estabilidad del origen del sistema dado por
x.1= -6x1/(1+x21)2 +2x2
x.2= -2(x1+x2)/(1+x12)2 (12)
Escogiendo w(x) = (1+x12)2 ≥ 0, y dado que V(x) es polinomio, en el algoritmo para encontrar la función de Lyapunov se define −(1+x12)2 δV/δx f (x) como una desigualdad SOS con la finalidad de cumplir la segunda condición del teorema general de estabilidad.El resultado de esta aplicación es una función V(x) de orden 10 con 62 términos. El diagrama de fase del sistema y algunas curvas de nivel de V(x) (i. e., regiones de atracción en el origen) se muestran en la Figura 2.
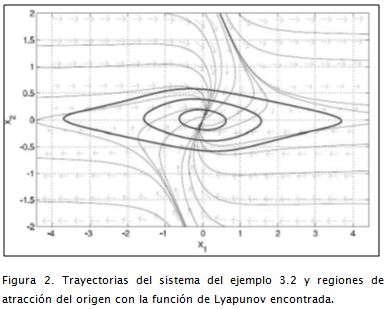
Se observa que en el sistema (12), el punto x = 0 es el único punto de equilibrio, y la determinación de V(x) permite establecer regiones de atracción en el origen.
A pesar de que las funciones de Lyapunov halladas para los ejemplos 3.1 y 3.2 tienen un elevado número de términos, poseen la ventaja de encontrarse directamente en el entorno del toolbox symbolic de Matlab, permitiendo facilidad en la manipulación, graficación y verificación de las condiciones de las expresiones.
Además, a partir de los ejemplos presentados se vislumbra la utilidad de la herramienta SOSTOOLS en el análisis de sistemas de mayor complejidad o de mayor cantidad de variables, simplificando el trabajo de la demostración de estabilidad a la implementación de algoritmos adecuados en la herramienta computacional.
Sistemas con incertidumbres en los parámetros
Considerar el sistema no lineal general dado por la ecuación (6), y que la incertidumbre en los parámetros del sistema puede ser expresada como:
ci(x,u)≤0 para i=1,...,N1 (13)
donde u ∈ Rm es el conjunto de parámetros con incertidumbre y N1 es el número de restricciones requeridas.
Asumir que las funciones ci pueden ser expresadas como funciones polinómicas en (x,u), y f (x,u) como un vector de funciones polinómicas o racionales en (x,u) sin singularidades en D ⊂ Rn×m, donde D = {(x,u) ∈ Rn×m|ci(x,u) ≤ 0, para todo i. Además, sin pérdida de generalidad, asumir que f (x,u) = 0 para
x = 0 y u ∈ D0 u , donde D0 u = {u ∈ Rm|(0,u) ∈ D}. El siguiente teorema, tomado de Papachristodoulou y Prajna (2002), que es una extensión del teorema de estabilidad de Lyapunov, presenta las condiciones para la estabilidad local del origen del sistema (6) con las restricciones dadas por (13).
Teorema 3.2. Suponiendo que para el sistema existen funciones V(x), w(x,u) y pi(x,u) tales que V(x) es positiva definida en una vecindad del origen w(x,u) > 0 y pi(x,u) ≥ 0 en D entonces
Z(x,u)=-w(x,u)δV/δx f(x,u)+∑i=1 N1p1(x,u)c1(x,u)≥0 (14)
garantiza que el origen es un punto de equilibrio estable del sistema.
Para el caso en que f (x,u) sea un campo vectorial racional, se escoge una función w(x,u) > 0 tal que −w(x,u)δV/δx f(x,u) sea una función polinómica y se puedan aplicar los algoritmos SOS. Las condiciones anteriores pueden ser relajadas a definiciones de SOS, como se muestra en la siguiente proposición tomada de Papachristodoulou y Prajna (2002).
Proposición 3.2. Para una función polinómica φ(x) ≥ 0 (o SOS), como se define en (7), la estabilidad local del origen del sistema puede ser garantizada si:
V(x)−φ(x) es SOS, es decir, V(x) es definida positiva. Z(x,u) es SOS.
pi(x,u), es SOS, para i = 1, . . . , N1 es SOS.
Entonces, el algoritmo para encontrar una función de Lyapunov conserva los tres primeros pasos del algoritmo para sistemas sin restricciones. Las diferencias se presentan al definir la condición (14). Para esto se debe:
En el siguiente ejemplo se aplica este procedimiento para evaluar la estabilidad del origen en un sistema térmico multizona con una estrategia de control basada en la teoría de juegos evolutivos (Pantoja y Quijano, 2008).
Ejemplo 3.3. Un sistema térmico con N zonas independientes puede ser modelado mediante
Ti=-aiTi+bixi+aiTa
donde Ti es la temperatura en la i- ésima zona (i = 1, . . . , N), ai,bi constantes positivas, Ta es la temperatura ambiente y xi es la entrada de control para la zona i. Asumiendo que Ti(0) = Ta, que se tiene una temperatura límite superior B tal que B >> Ta, y haciendo qi = B−Ti, el sistema puede ser expresado por:
qi.= -aiqi-bixi+ai(B-Ta) (15)
Las dinámicas de la señal de control se definen de tal forma que la temperatura de todas las zonas llegue a un punto de equilibrio que corresponda a la máxima temperatura uniforme que se pueda obtener a partir de una cantidad de recursos limitada. Estas dinámicas, dadas por el concepto de replicator dynamics (Pantoja y Quijano, 2008), son:
x1.= x1 (q1-1/P∑j=1Nxjqj) (16)
donde P > 0 es la cantidad total de recursos disponibles para calentar todas las zonas. Entonces,∑j=1Nxi= P. El punto de equilibrio del sistema compuesto por (15) y (16) es:
x*1=aj/bjP/∑j=1N aj/bj
q*1= (B-Ta)- P/∑j=1N aj/bj
de donde la temperatura final de cada zona está dada por
T1*= Ta+P/∑j=1N aj/bj, para 1=1, ...,N
que es claramente constante y dependiente solamente de los parámetros del sistema y de los recursos disponibles.
El problema radica entonces en analizar la estabilidad de este punto de equilibrio ante variaciones en los parámetros de cada zona ai y bi para un sistema de dos zonas (i.e., N = 2).
Al realizar un cambio de coordenadas en el sistema para que el origen sea el punto de equilibrio, las variables de error del sistema están definidas por eqi = qi−q*iy exi= xi−x*i. Dado que x1 + x2 = P, x*2 = P−x*1, luego ex2 = −ex1 . Entonces, el sistema descrito por
e.1= (ex1+Pa1b2/a1b2+a2b1)(eq2-eq1)...
(a1b2/a1b2+a2b1 + ex1/P -1)
e.q1=-a1eq1-b1ex1e.q2= -a2eq2+b2ex1
tiene al origen como el único punto de equilibrio.
Unos rangos estimados de las variaciones en los parámetros del sistema están dada por:
0 < ai< 2 para i = 1,2
0 < bi < 0,01 para i = 1,2
Estas desigualdades deben expresarse de forma polinómica para incluirse en el algoritmo SOS. Para esto, sean a y a los límites inferior y superior respectivamente para la variable a, la desigualdad a < a < a se expresa como (a−a)(a−a) < 0. Definiendo además los polinomios respectivos pi(x,u) como variables polinómicas SOS y w(x,u) = (a1b2+a2b1)2 > 0, se adecúa la condición (14) a una desigualdad SOS para implementar el algoritmo en SOSTOOLS.
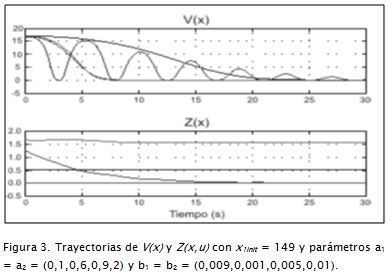
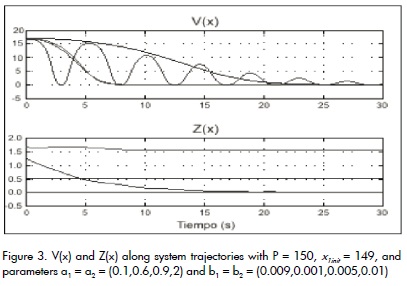
El resultado del programa es una función en V(x) de orden 4 con 32 términos, cuyas trayectorias a lo largo de las soluciones del sistema se muestran en la Figura 3, para diferentes valores de los parámetros aiy bi, con una cantidad de recursos P = 150 y con señal de control inicial x1 = 149. En esta misma figura se presenta el comportamiento de Z(x,u) para iguales condiciones.
Se debe notar que con la finalidad de cumplir con las condiciones del teorema 3.1, las trayectorias de estas funciones sólo deben ser mayores que cero. Cuando los valores de los parámetros se acercan a los límites de los rangos establecidos, Z(x,u) se acerca a cero más rápidamente.
Esto implica la proximidad de la restricción y la necesidad de establecer nuevos rangos para obtener una nueva función de Lyapunov. En cuanto a los resultados mostrados en la Figura 3, el punto de equilibrio del sistema térmico multizona controlado es asintóticamente estable, como se demuestra en Pantoja y Quijano (2008).
Sistemas conmutados
En esta sección se considera el problema del análisis de estabilidad de los sistemas conmutados (i. e., sistemas continuos con señales de conmutación) usando desigualdades de disipación con conmutaciones arbitrarias.
Este método permite encontrar una función común de Lyapunov para todo el conjunto de subsistemas.
El resultado principal que permite usar el método de las desigualdades de disipación, desarrollado previamente para sistemas no lineales de forma polinomio, es una nueva representación del sistema conmutado como un sistema polinomio continuo con restricción, es decir que el sistema conmutado original es representado por un sistema de ecuaciones diferencio-algebraicas DAE (Differential-Algebraic Equations), donde todas las ecuaciones diferenciales y algebraicas son de forma polinomio (Mojica-Nava et al., 2010).
3.3.1 Aproximación en polinomio de los sistemas conmutados. Se define a los sistemas conmutados como aquellos que consisten de varios subsistemas continuos y una ley de conmutación discreta que indica cuál estado está activo en cada instante de tiempo.
El modelo matemático que describe los sistemas conmutados de forma general está dado por
x.(t)=fσ(t)(x,u,t) (17)
donde fi : Rn×Rm×R+→Rnson los vectores de campo, la entrada externa de control u ∈ Rmy s : [0, t f ] → Q ∈ {0,1,2, ...,q} es un función del tiempo constante a trozos. Cada modo de operación corresponde a un sistema específico ˙ x(t) = fi(x,u, t), para algún i ∈ Q, y la señal de conmutación s determina cuál subsistema es seguido en cada instante del tiempo, dentro del intervalo de tiempo [0, t f ], con t f como tiempo final. Las señales de control, σ y u, son funciones medibles.
Esta definición general de sistemas conmutados permite obtener una representación en polinomio continua, como se mencionó, definiendo una nueva variable, la cual cumple las funciones de variable de control, reemplazando la señal de conmutación por una señal continua pero restringida a tomar ciertos valores dentro del conjunto de valores posibles. Para hacer esto lo primero es reescribir la ecuación (17) como un sistema no conmutado controlado.
Primero, se define un vector de campos vectoriales F(x,u) : Rn×Rm→Rn,
F(x,u)=[f0(x,u)f1(x,u)...fq(x,u) (18)
donde fi(x,u), i ∈Q es la función para cada subsistema del sistema conmutado dado en (17). Luego, para encontrar la expresión en polinomio se necesita en cada i ∈ Q = {0,1, . . . ,q} un coeficiente lk con la propiedad de lk(i) = 0 cuando i 6= k, y lk(k) = 1. Sea L el vector de coeficientes de interpolación en polinomio de LaGrange (Burden y Faires, 1985) definido con la nueva variable s, i. e.:
L(s)=[l0(s),l1(s),...,lq(s)]T (19)
donde
lk(s)= Πqi=0,l=/k(20)
Por otro lado, se necesita restringir los valores de la variables para que lleve al sistema a estar en las mismas posibles trayectorias del sistema conmutado; esto se logra gracias a un polinomio cuyas raíces corresponden con los números de posible modos de operación. Sea Q(s) el polinomio que restringe, tal que
Q(s)=Πqk=0 (s-k) =0 (21)
Un sistema polinomio continuo relacionado con el sistema conmutado original (17) está definido en la siguiente proposición, tomada de Mojica-Nava et al. (2010).
Proposición 3.3. Considere un sistema conmutado de la forma presentada en (17), con un vector de campos vectoriales en la forma dada en (19) tal que existe un único polinomio P de orden q+1 con la propiedad de fi(x,u) = P(x,u, i) para cada i ∈ Q. Este polinomio está dado por
P(x,u,s)= F(x,u)L(s)
= ∑qk=0 fk(x,u)lk(s) (22)donde s ∈ R, y lk(s) es dado por (21). Ahora, el sistema (17) toma la forma del sistema continuo polinomio con restricciones, representado por un sistema de ecuaciones algebro-diferenciales no lineales
x.=P(x,u,s)
0=Q(s) (23)
por cada i ∈ Q = {0,1, ...,q} sujeto al polinomio Q(s) dado en (21).
Ahora, la representación polinomio permite tratar el problema con las técnicas descritas para sistemas poligonales usando la teoría de las desigualdades de disipación. Es conveniente aclarar en esta parte que esa representación polinomio también puede ser usada para hallar la función común de Lyapunov por los métodos planteados, pero se presentan las desigualdades de disipación para abrir posibilidades a futuros trabajos en el área del análisis de disipación de energía en los sistemas conmutados, un tema que no ha sido ampliamente desarrollado (Zhao y Hill, 2008).
En la siguiente sección se presentan los principales resultados obtenidos sobre el análisis de estabilidad de sistemas conmutados usando las desigualdades de disipación.
3.3.1. Resultados en análisis de estabilidad usando las desigualdades de disipación
El siguiente teorema (tomado de Ebenbauer y Allg¨ower, 2004) da un resultado simple para la estabilidad de sistemas modelados por ecuaciones algebro-diferenciales del tipo (23).
Teorema 3.4.El punto de equilibrio x = 0 del sistema algebro-diferencial (23) es estable para cualquier entrada admisible s = s(t), si existe una función de Lyapunov candidata V : Rn 7→ R, una función r : R(m+2)(n+q) 7→ R, y un número entero m tal que la desigualdad de disipación
∀ V(x)x.≤ //Gμ(ξ,ς) (24)
es satisfecha por algún x-vecindario Ωx((ξ ,ς) = 0).
La idea detrás de la desigualdad (24) no es más que la verificación de que la función ˙V sea negativa, semidefinida con respecto al conjunto de restricciones.
En general es difícil encontrar una función de Lyapunov V y una función r para problemas por acticos. Pero justamente los desarrollos que han tenido las técnicas SOS basadas en programación semidefinida permiten verificar las desigualdades de la forma (24) eficientemente en el caso de que todas las funciones implicadas en la desigualdad tengan forma polinomio (Ebenbauer y Allg¨ower, 2004). Ciertamente, en este caso, todas las funciones son de naturaleza polinomio. Ya ha sido establecido que el sistema algebro-diferencial (23) es de índice 1 (Mojica-Nava et al., 2010). Así que se debe escoger m = 1, y si se trata de probar la estabilidad global del sistema (22), la siguiente desigualdad polinomio debe ser satisfecha:
V(x) > 0
∀ V (x) P(x,s) ≤ //Q(s)//2ρ(x,s)lo cual implica que
V(x) > 0
∀ V (x)( ∑qk=0fk(x,u)lk(s))≤ //Πqk=0 (s-k)//2ρ(x,s)(25)
para todo x = (x, ˙ x, s) ∈ R2n. Nótese que si V es polinomio y positiva definida, implica que V es radialmente ilimitada.
Por ilustración y claridad de exposición, se considera el caso cuando q = 1. La desigualdad de disipación es de la forma
∀ V (x)(f0(x)(1-s)+f1(x)s≤//s(1-s)//2ρ(x,s)(26)
Usando los conceptos sobre SOS se puede presentar la desigualdad (25) como sigue.
Encontrar una función polinomio V(x) tal que
V(x)-φ(x)≥0 es SOS
-∀ V (x)(∑qk=0fk(x,u)lk(s))+...
//Πqk=0 (s-k)//2ρ(x,s)≥0 es SOS (27)
las funciones poligonales V(x), r (x, s), y la función definida positiva j(x) puede ser computada usando SOSTOOLS (Prajna et al.).
3.3.3. Ejemplo numérico: sistema conmutado. Se considera el sistema conmutado siguiente: ˙ x = fi(x), x = [x1 x2]T, con

Este sistema está considerado como conmutado homogéneo presentado para análisis de estabilidad (Zhang et al., 2007). Con el propósito de probar estabilidad bajo conmutaciones arbitrarias, se usa la representación equivalente polinomio
x.(t)=f0(1-s)+f1s
s∈Γ ={s∈R/Q(s)=s(s-1)=0
Usando estas matrices poligonales se obtiene,
-δV/δxf0(1-s)+f1(s)+(s4-2s3+s2)λ(x,s)≥0
Utilizando SOSTOOLS se obtiene una función de Lyapunov de grado sexto, i. e.:
V(x)= -0,0364x21+0,02x41-0,0082x42+0,0476x22...
-0,056x1x2+0,0113x21x22-0,064x1x32-0,0457x61
...-0,016x41x42+0,0034x62
la cual, a través del teorema 3.5, prueba que el origen del sistema conmutado homogéneo no lineal reformulado como una DAE polinomio es estable.
Conclusiones
En este tutorial se presentan las técnicas SOS como un criterio efectivo para la demostración de no negatividad de funciones polinómicas multivariables. Aunque la determinación de la no negatividad de una función polinómica puede resultar en un problema NPHard, al plantear las condiciones de estabilidad por medio de variables SOS el problema puede ser resuelto eficazmente por el toolbox SOSTOOLS, teniendo en cuenta los posibles errores numéricos y el elevado costo computacional de esta herramienta en sistemas con un número de variables elevado. A partir de considerar sistemas no lineales polinomios se pueden realizar extensiones al análisis de sistemas racionales resultantes de controladores no lineales y de sistemas conmutados analizados desde un enfoque polinomio, teniendo en cuenta las variaciones e incertidumbres en los parámetros del sistema o restricciones en el procedimiento de análisis de estabilidad. De esta manera, a partir de los ejemplos presentados, se vislumbra la utilidad de las herramientas SOS en el análisis de sistemas de diferentes tipos o de mayor complejidad.
BibliografíaAnjos, M., Burer, S., On handling free variables in interior-point methods for conic linear optimization., SIAM Journal on Optimization, 18(4), 2007, pp.1310-1325.
Burden, R., Faires, J. D., Numerical Analysis PWS, Boston, 1985.
Ebenbauer, C., Allgöwer, F., Computer-Aided Stability Analysis of Differential-Algebraic Equations., In Proceedings of the NOLCOS, 2004, pp. 1025-1030.
Ebenbauer, C., Allgöwer, F., Analysis and Design of Polynomial Control Systems Using Dissipation Inequalities and Sum of Squares., Computers & Chemical Engineering, 30 (10-12), 2006, pp. 1590- 1602.
Franze, G., Casavola, A., Famularo, D., Garone, E., An off-line MPC Strategy for Nonlinear Systems Based on SOS Programming., Nonlinear Model Predictive Control, LNCIS 384, 2009, pp. 491-499.
Khalil, H., Nonlinear Systems., Prentice Hall Upper Saddle River, NJ, 2002.
Mojica-Nava, E., Quijano, N., Rakoto- Ravalontsalama, N., Gauthier, A., A Polynomial Approach to Stability Analysis of Switched Systems., Systems and Control Letters, 59(2), 2010, pp. 98-104.
Pantoja, A., Quijano, N., Modeling and Analysis for a Temperature System Based on Resource Dynamics and the Ideal Free Distribution., In Proceedings of the American Control Conference, 2008, pp. 3390-3395.
Papachristodoulou, A., Analysis of Nonlinear Time- Delay Systems Using the Sum of Squares Decomposition., In Proceedings of the American Control Conference, 2004, pp. 4153-4158.
Papachristodoulou, A., Prajna, S., On the Construction of Lyapunov Functions Using the Sum of Squares Decomposition., In Proceedings of the 41st IEEE Conference on Decision and Control, 2002, pp. 3482-3487.
Parrilo, P., Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization., Ph.D. thesis, California Institute of Technology, 2000.
Parrilo, P., Semidefinite Programming Relaxations for Semialgebraic Problems., Mathematical Programming, 96(2), 2003, pp. 293-320.
Prajna, S., Papachristodoulou, A., Parrilo, P., SOSTOOLS: Sum of Squares Optimization Toolbox for MATLAB-User Guide., Control and Dynamical Systems, California Institute of Technology, Pasadena, CA, 91125. Available on http://www.cds.caltech.edu/sostools.
Prajna, S., Papachristodoulou, A., Seiler, P., Parrilo, P., SOSTOOLS: Control Applications and New Developments., In Proceedings of the IEEE International Symposium on Computer Aided Control Systems Design, 2004, pp. 315-320.
Reznick, B., Some Concrete Aspects of Hilberts 17th Problem., Contemporary Mathematics, 253, 2000, pp. 251-272.
Topcu, U., Packard, A., Local Stability Analysis for Uncertain Nonlinear Systems., IEEE Transactions on Automatic Control, 54(5), 2009, pp. 1042-1047.
Topcu, U., Packard, A., Seiler, P., Local Stability Analysis Using Simulations and Sum-of-SquaresProgramming,, Automatica, 44(10), 2008, pp. 2669- 2675.
Zhang, L., Liu, S., Lan, H., On Stability of Switched Homogeneous Nonlinear Systems., J. Math. Anal. Appl, 334, 2007, pp. 414-430.
Zhao, J., Hill, D., Passivity and Stability of Switched Systems: A Multiple Storage Function Method., Systems & Control Letters, 57, 2008, pp. 158- 164.
Andrés Pantoja1 , Eduardo Mojica Nava2 y Nicanor Quijano3
1 Electronic Engineering, Universidad Nacional de Colombia Sede Manizales. M.Sc., in Electronic Engineering, Universidad de los Andes. Ph. D., Student, Universidad de los Andes. Universidad de Nariño, Pasto. ad.pantoja24@uniandes.edu.co
2Electronic Engineering, Universidad Industrial de Santander. M.Sc., in Electronic Engineering, Universidad de los Andes. Ph.D., in Engineering, Universidad de los Andes y Ecole Centrale Nantes, Francia. Universidad Católica, Bogotá, Colombia. ea.mojica70@uniandes.edu.co
3Electrical Engineer, Pontificia Universidad Javeriana, Bogotá, Colombia. M.Sc.,and Ph.D., in Electronic Engineering, Ohio State University, Columbus, OH,USA. Universidad de los Andes, Bogotá, Colombia. nquijano@uniandes.edu.co
ABSTRACT
The sum of squares (SOS) decomposition technique allows numerical methods such as semidefinite programming to be used for proving the positivity of multivariable polynomial functions. It is well known that it is not an easy task to find Lyapunov functions for stability analysis of nonlinear systems. An algorithmic tool is used in this work for solving this problem. This approach is presented as SOS programming and solutions were obtained with a Matlab toolbox. Simple examples of SOS concepts, stability analysis for nonlinear polynomial and rational systems with uncertainties in parameters are presented to show the use of this tool. Besides these approaches, an alternative stability analysis for switched systems using a polynomial approach is also presented.
Keywords: sum of squares (SOS), stability analysis, nonlinear systems, switched systems.
Received: april 30th 2009
Accepted: november 15th 2010
Introduction
The theory of sum of squares (SOS) decomposition of polynomial functions has achieved significant progress during the last ten years since its introduction (Parrilo, 2000). This development has resulted from possible relaxations of NP-hard problems (e.g., non-negativity proofs of multivariable polynomials) (Papadimitriou, 1994) for solvable problems in computational polynomial time. The basic problem consists of finding conditions to verify. The possible classes of F functions must be limited to study this problem from an algorithmic approach and, at the same time, to keep the problem general enough to guarantee the applicability of the results. A tradeoff is achieved when the class of F functions is restricted to polynomial functions (Parrilo, 2000)
F(x1,...,xn)≥0, ∀x1,...,xn∈Rn (1)Definition 1.1. A polynomial function f in x1, . . . , xn, with coefficients in a field k, is a finite lineal combination of monomials:
f= ∑αcαxα=∑αcαx1α1...xnαn cα>k (2)
where the sum is given over a finite number of n -− tuples
α = (α1, ..., αn), con αi∈ N0.
It is possible to show that proving polynomial function global positivit is in fact an NP-hard problem too (when the degree of the function is at least four). Therefore, a method guaranteeing the solution of this problem for any polynomial function could have unacceptable computational performance for a function having a high number of variables. This is the main disadvantage of theoretical methods so that the quantifiers are eliminated (Parrilo, 2000).
A question arises when inherent computational complexity problems must be avoided. Do some conditions guarantee the positivity of a multivariable function so that the method can be executed in polynomial time? The next section shows that SOS descomposition techniques fulfil complexity reduction conditions.
Some SOS technique applications are global, boolean and constrained optimization problems (Prajna et al., 2004). Moreover, some general control problems, such as Lyapunov´s function construction for stability analysis of nonlinear systems (Topcu et al.,2008) and parameter uncertainty limitation in dynamic system analysis (Topcu and Packard, 2009) have been solved using the SOS approach. Other specific control applications are stability analysis of nonlinear systems with time delay (Papachristodoulou, 2004) and the synthesis and design of nonlinear controllers (Franze et al., 2009; Ebenbauer and Allg¨ower, 2006).
SOS techniques solve a convex optimisation problem by means of semidefinite programming (SDP) (Parrilo, 2003). This method is a generalisation of linear programming (LP) where non-negativity constraints in decision variables are replaced by positive semidefinite matrix inequalities. The methods for solving SDP are given by algorithmic techniques such as linear matrix inequalities (LMI) and numerical programmes for SDP such as SeDuMi and SPDT3 (Anjos and Burer, 2007).
Solving an SOS problem implies SDP problem construction, finding the numerical solution, and interpreting the result of the SDP problem in initial variable formulation. The Matlab toolbox SOSTOOLS (Prajna et al.,) was used for defining SOS variables,functions and constraints needed for resolving the optimisation problem in a symbolic environment.
This tutorial presents and reviews the basic concepts of SOS techniques and some control applications such as Lyapunov function construction for stability analysis of nonlinear systems, parameter uncertainty analysis in systems having rational vector fields, application in stability analysis of switching systems and the use of SOSTOOLS for solving some problems and examples.
Sum of squares (SOS)
The main concepts and basic examples of SOS techniques are presented in this section. As stated, these concepts were originally introduced by P. Parrilo (Parrilo, 2000). The examples start with SOS decomposition of a multivariable polynomial function to introduce some control applications.
The Matlab toolbox SOSTOOLS is introduced as a computational method used in the numerical solution of SOS problems introduced in this tutorial.
Basic concepts
Definition 2.1. A multivariable polynomial p(x) having degree 2d in x ∈ Rn, is a sum of squares (SOS) if there exists M polynomials fi(x) so that
p(x)= ∑i=1M f12(x) (3)
SOS decomposition can be expressed as shown by Parrilo (2003) if there is a positive semidefinite matrix Q ∈ Rn×n, so that
p(x)=Z(x)T QZ(x) (4)
where Z(x) is a vector of monomials in x with a degree less than or equal to d. Given that Q = Q,T _ 0 can be written as Q = HHT, where H ∈ Rn×r with r = rank(Q), and if h1, h2, . . . , hr, are the columns of H, then equation (4) can be expressed as
p(x)= ∑i=1 (hT1Z(x))2 (5)
Therefore, SOS decomposition can be relaxed to find matrix Q _ 0 and the resulting problem becomes a semidefinite programming issue as defined by Parrilo (2000).
The next example presents the representation of a polynomial function in an SOS form expressed as in equations (4) and (5).
Example 2.1. Find SOS decomposition of the polynomial function given by
p(x) = 13x41+14x31x2-18x21+14x21x22...
...6x1x2+9x42-30x32x1+9With a vector
Z(x) = [1 x22 x1x2 x12]T
a matrix QT≥ 0 is found so that

Then, with factorisation Q =HHT given by
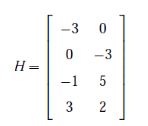
The resulting SOS decomposition is
p(x)= (3x12-x1x2-3)2 + (2x21-3x22+5x1x2)2
Clearly an SOS function is globally positive, but not all positive functions are SOS.
An example of these functions would be the Motzkin polynomial M(x) = x41 x22+x21x42+x63−3x21x22x23. To prove positivity in this class of functions using SOS techniques, Reznick (2000) has shown that if p(x) > 0, for all x ∈ Rn, then there exists a positive integer r so that
p(x)(∑ni=1x21)r is SOS
The non-negativity problem is relaxed for testing different values of r until SOS representation is possible.
SOSTOOLS computational tool
SOSTOOLS (Prajna et al.,) is a Matlab toolbox which is used to solve SOS problems with an algorithm for semidefinite programming(e.g., SeDuMi or SDPT3).This tool turns the SOS problem into an SDP problem, uses the solving algorithm and expresses the solution in the initial variables and polynomials. The general procedure for obtaining SOS problem solution using SOSTOOLS is summaryzed as follows:
- Define SOS variables, polynomials and constants using the symbolic toolbox, or in Matlab polynomial format;
- Define the problem´s constraints as SOS inequalities; and
- Use the SOSTOOLS functions for solving the problem and for expressing the solution in the problem´s initial variables.
The next section presents some control applications which use SOS techniques to obtain a Lyapunov function which can be used for the stability analysis of the equilibrium point for nonlinear and switched systems
Control applications
Finding a Lyapunov function to prove the stability of an equilibrium point in a nonlinear system is a difficult task, except for systems having few variables and special vector fields (e.g., energy functions and gradient systems), where specific methods (e.g., Krasovskii) could be used (Khalil, 2002).
For more general systems, SOS techniques facilitate finding an appropriate Lyapunov function using a computational tool and fixed algorithm. The conditions for verifying the stability of an equilibrium point in systems having polynomial and rational vector fields rely on non-negative functions which could result in NPHard problems. Therefore, by turning these conditions into SOS functions, the problem can be solved using the SOSTOOLS computational tool.The tool is applied to polynomial and rational systems having parameter uncertainties in the next examples using variations of the simple original algorithms and extensions of the fundamental theorems in Lyapunov analysis.
Systems having polynomial and rational vector fields
The Lyapunov stability theorem is applied to the general autonomous system given by
x.=f(x) (6)
where f : D →Rn is a continuous map from D ⊂ Rnen Rn, and without loss of generality (Khalil, 2002), the origin is an equilibrium point of (6) (i.e., f (0) = 0). If a continuously differentiable function V(x) (so-called Lyapunov function) is found, the system´s stability conditions are defined by: i) if V(x) is positive definite, and ii) V(x) is negative semidefinite, the origin of (6) is stable; and ii) if V(x) is negative definite, the origin is asymptotically stable.
This theorem´s conditions must be relaxed to apply the SOS techniques for proving stability in nonlinear systems to express non-negativity as SOS. In polynomial systems having state variables x = [x1, x2, . . . , xn], a function V(x) with degree 2d is defined using an auxiliary function φ(x) given by
φ(x)= ∑i=1n ∑nj=1εijx12j (7)
where e ε ≥ 0, for all i and j, and ∑aj=1εij> 0, for alli = 1,2, . . . ,n. With these conditions, j(x) is positive definite. Therefore, if V(x)−φ(x) can be expressed as SOS, it is guaranteed that V(x) is positive definite too. Stability conditions can then be expressed as:
V(x)−φ(x) es SOS (8)
- δV/δx f(x) es SOS (9)
Hence, the SOS algorithm for finding a Lyapunov function using SOSTOOLS is stated as follows:
- Define a general polynomial function V(x) with degree 2d and monomials in x with degree d;
- Create the auxiliary function φ(x) as defined in (7);
- Define the expression V(x)−φ(x) as SOS. Inequality;
- Define - δV/δx f (x) as SOS inequality; and
- Solve the SOSTOOLS programme and obtain the resulting V(x).
Example 3.1. (Khalil, 2002). Find a Lyapunov function to show asymptotical stability of the origin in the system:
x.1= x2(1-x21)
x.2= -(x1+x2)(1-x21) (10)The system has an equilibrium point in x = 0. This equilibrium is not the only one, given that in x1 = 1 y en x1=−1, x1=0 and x2=0. Then, finding a Lyapunov function that satisfies conditions (8) and (9) is not an easy task for analysing the origin´s characterristics. Moreover, a region of attraction can be determined using the contour lines of the function V(x) so obtained.
Using SOSTOOLS, a function having 42 terms and degree 8 is found. Figure 1 shows the system´s phase plane and the contour lines of V(x). It is shown that the biggest region of attraction is obtained when the contour lines approximate to x1 = −1, which is thelimit where the isoclines of the Lyapunov function are closed.

In a system having a rational vector field f (x), condition (9) is modified to apply the SOSTOOLS algorithm. In this case, a function w(x) > 0 must be found so that
-w(x)- δV/δx f(x) sea SOS and polynomial (11)
If w(x) > 0, the second condition of the general stability theorem is satisfied, and if (11) is a polynomial function, the SOS techniques can be applied as shown in the next example.
Example 3.2. (Khalil, 2002). Find a polynomial Lyapunov function to show stability of the origin of the system given by
p>x.1= -6x1/(1+x21)2 +2x2x.2= -2(x1+x2)/(1+x12)2 (12)
Choosing w(x) = (1+x21)2 ≥ 0, and given that V(x) is a polynomial function, the algorithm for finding the Lyapunov function must include −(1+x12)2 δV/δx f (x) as SOS inequality to satisfy the second condition of the stability theorem.
The result of this SOSTOOLS programme is a function V(x) with 62 terms and degree 10. The phase plane and some contour lines of V(x) (i.e., regions of attraction of the origin) are shown in Figure 2.

The system in (12) has a unique equilibrium point in x = 0, and the Lyapunov function obtained leads to establishing regions of attraction for the origin.
Although the Lyapunov functions found in examples 3.1 and 3.2 have a high number of terms, these functions are in the Matlab symbolic environment which facilitates plotting and verifying stability conditions.
Besides, the examples presented here have given a glimpse of the use of SOS techniques for analysing more complex and higher order systems.
Systems with parameter uncertainties
Consider the general nonlinear system given by equation (6) with parameter uncertainties expressed as
ci(x,u)≤0 para i=1,...,N1 (13)
where u ∈Rm is the set of uncertain parameters, and N1 is the number of required constraints.
Assume that functions ci can be expressed as polynomial functions in (x,u), and that f (x,u) is a rational or polynomial vector field in (x,u) without singularities in D ⊂ Rn×m, where D = {(x,u) ∈ Rn×m|ci(x,u) ≤ 0, for all i. Without loss of generality, it is assumed that f (x,u)= 0 for x = 0 and u ∈ D0 u , donde D0 u = {u ∈ Rm|(0,u) ∈ D}.The following theorem taken from Papachristodoulou and Prajna (2002) gives us the conditions for local stability of the origin of the system (6) constrained by (13).
Theorem 3.1. Suppose that for the system described above, there are polynomial functions V(x), w(x,u), and pi(x,u) so that: V(x) is positive definite in a neighbourhood of the origin, w(x,u) > 0 and pi(x,u) ≥ 0 in W Then, if
it guarantees that the origin of the state space is a stable equilibrium of the system (6). In the case where f (x,u) is a rational vector field, a function w(x,u) > 0 must be chosen so that −w(x,u)δV/δx f(x,u) is a polynomial function, and SOS algorithm can be applied without additional modifications. These conditions can be relaxed to SOS definitions according to the following proposition taken from Papachristodoulou and Prajna (2002).
Proposition 3.2. For a polynomial function φ(x) ≥ 0 (or SOS) defined as in equation (7), the local stability of the origin of (6) can be guaranteed if:
V(x)−φ(x) is SOS (i.e., V(x) is positive definite). Z(x,u) is SOS.
pi(x,u), is SOS, for i = 1, . . . , N1.
Using this proposition, the algorithm to find the Lyapunov function preserves the first three steps used in systems without constraints. The differences for systems with parameter uncertainties are defined for the condition given by (14). The next steps are required for this definition:
- Define a number of SOS functions pi(x,u) equal to the number of inequality constraints in the problem;
- Choose a function w(x,u) > 0 if necessary for a rational vector field f (x,u);
- Define −w(x,u)δV/δx f(x,u) + ∑ pi(x,u)ci(x,u) as SOS inequality; and
- Solve the SOSTOOLS problem and obtain V(x).
The next example applies the previously described procedure for evaluating the stability of the equilibrium point in a multi-zone thermal system with a controller based on evolutionary game theory (Pantoja and Quijano, 2008).
Example 3.3. A system with multiple disjoint temperature zones can be modelled by
Ti=-aiTi+bixi+aiTa
where Ti is the temperature in the ith zone (i = 1, . . . ,N), ai,bi are positive constants, Ta is ambient temperature and xi is control input for zone i. Assuming that B is a temperature limit so that B >> Ta, and with variable change qi = B−Ti the system can be expressed by:
qi.= -aiqi-bixi+ai(B-Ta) (15)
The control signal dynamics are designed so that the temperature in all zones achieves an equilibrium point equal to the maximum uniform temperature that can be obtained with a limited amount of power resources. The control strategy is given by the replicator dynamics concept (Pantoja and Quijano, 2008):
x1.= x1 (q1-1/P∑j=1Nxjqj) (16)
where P > 0 is the total available amount of resources for heating all zones. Then ∑j=1Nxi= P. The equilibrium point of the complete system composed by equations(15) and (16) is:
x*1=aj/bjP/∑j=1N aj/bj
q*1= (B-Ta)- P/∑j=1N aj/bj
The final temperature in each zone is given by:
T1*= Ta+P/∑j=1N aj/bj, para i =1, ...,N
which is clearly constant and depends on the system´s parameters and on the available resources.
The proposed problem is to analyze the stability of the equilibrium point, given limited variations in the parameters of each zone ai and bi for a two-zone system (i.e., N = 2).
To express the system in "error coordinates" so that the equilibrium point is displaced to the origin, the displacement variables are eqi = qi−q*iy exi= xi−x*i. Taking into account that x1 + x2 = P, x*2 = P−x*1,, then ex2 = −ex1. With these conditions, the system is given by:
e.1= (ex1+Pa1b2/a1b2+a2b1)(eq2-eq1)...
(a1b2/a1b2+a2b1 + ex1/P -1)
e.q1=-a1eq1-b1ex1e.q2= -a2eq2+b2ex1
and the origin is the unique equilibrium point.
Appropriate estimated ranges for the parameters´ variations are:
0 < ai< 2 para i = 1,2
0 < bi < 0,01 para i = 1,2
These inequalities must be expressed in polynomial form to be included in the SOS algorithm. For this purpose, if we assume that a and a are the lower and higher limits for a, respectively, inequality a < a < a is expressed as (a−a) (a−a) < 0. Defining polynomials pi(x,u), for i = 1,2 as SOS variables, and w(x,u) = (a1b2+a2b1)2 > 0, condition (14) is implemented as SOS inequality in the SOSTOOLS algorithm.
The resulting V(x) is a Lyapunov function with 32 terms and 4 degrees whose trajectories throughout the system´s solutions are shown in Figure 3 for different parameter values within the specified ranges, with P = 150, and initial condition x1 = 149. Moreover, this Figure presents the trajectories of Z(x,u) for the same conditions.
It is interesting to notice that V(x) and Z(x,u) just need to be positive to satisfy the conditions in Theorem 3.1. Near the fixed limits of uncertainty, the functions are close to zero, showing the activation of the constraints and the need for finding another Lyapunov function for a wide range of uncertainties.
With the results presented in Figure 3, the equilibrium point of the controlled multi-zone temperature system is asymptotically stableas shown in Pantoja and Quijano (2008).
Switched systems
This section deals with switched systems´ stability analysis (i.e. continuous systems having switching signals) using dissipation inequalities under arbitrary switching.
This method leads to finding a common Lyapunov function for switched systems.
An efficient numerical method is presented using the simple stability result for stability analysis of polynomial differential-algebraic equations (Mojica- Nava et al., 2010).
Polynomial approach for switched systems: A switched system is a system that consists of several continuous-time systems with discrete switching events. A switched system may be obtained from a hybrid system by neglecting the details of discrete behaviour and instead considering all possible switching patterns from a certain class. The mathematical model can be described by
x.(t)=fσ(t)(x,u,t) (17)
where fi : Rn×Rm×R+→Rn are vector fields, exogenous input u ∈ Rm and σ [0, tf ] → Q ∈ {0,1,2,...,q} is a piecewise constant function of time. Every mode of operation corresponds to a specific subsystem ˙ x(t) = fi(x,u, t), for some i ∈ , and the switching signals determine which subsystem is followed at each point in time, into interval of time [0, tf], with tf as final time. The control inputs, σ and u, are both measurable functions.
This general definition of switched systems leads to obtaining a polynomial expression that is able to mimic switched system behaviour which is developed using a new variable s, which works as a ontrol variable or a parameter. The starting point is to rewrite (17)
as a continuous non-switched control system in its more general case.
First, a drift vector field F(x,u) : Rn×Rm →Rn
F(x,u)=[f0(x,u)f1(x,u)...fq(x,u) (18)
is defined where fi(x,u), i ∈Q is the function for each subsystem of the switched systems given in (17). Now, to find a polynomial expression, we need for each i ∈ Q = {0,1,. . . ,q}, a quotient lk with the property that lk(i) = 0 when i ≠ k, and lk(k) = 1. Let L be the vector of Lagrange polynomial interpolation quotients (Burden and Faires, 1985) defined with the new variable s, i.e.
L(s)=[l0(s),l1(s),...,lq(s)]T (19)
Where
lk(s)= Πqi=0,l=/k(20)
On the other hand, a complementary polynomial can be used to constrain s to take only integer values. Let Q(s) be the constraint polynomial so that
Q(s)=Πqk=0 (s-k) =0 (21)
A related continuous polynomial system of the switched system(17) is constructed in the following proposition taken from Mojica- Nava et al. (2010).
Proposition 3.3. Consider a switched system of the form given in(17) with a drift vector field which are in the form given in (19). Then, there exists a unique polynomial P of order q+1 with property f. This polynomial is given by
P(x,u,s)= F(x,u)L(s)
= ∑qk=0 fk(x,u)lk(s) (22)
where s ∈ R, and lk(s) is given by (21). Now, the system (17)takes the constrained continuous form of a non-linear differential algebraic equation
x.=P(x,u,s)
0=Q(s) (23)
for each i ∈ Q = {0,1,...,q} subject to the constraint polynomial Q(s) given in (21).
Polynomial representation means that the approach presented recently for constrained polynomial control systems based on dissipation inequality can now be applied. Notice that this polynomial representation can also be used for finding a common Lyapunov function using traditional methods, but dissipation inequalities are used to provide possibilities for future work in analysing energy dissipation in switched systems, a topic which has not been widely studied (Zhao and Hill, 2008).
The next section presents the main results obtained for stability analysis of switched systems using dissipation inequalities.
Results in stability analysis using dissipation inequalities
The following theorem taken from Ebenbauer and Allgower (2004)gives a simple stability result for the general differential-algebraic systems of type (23).
Theorem 3.4. Equilibrium point x = 0 from the differential-algebraic system (23) is stable for any admissible input s = s(t), if there exists a Lyapunov function candidate V : Rn → R, a function ρ: R(μ+2)(n+q) → R, and an integer number μ so that dissipation inequality
∀ V(x)x.≤ //Gμ(ξ,ς) (24)
is satisfied for some x-neighbourhood Ωx((ξ ,ς) = 0).
The main idea behind inequality (24) is just to check negative emidefiniteness of ˙V regarding the constraint set.
It is very difficult to search for a Lyapunov function V and a function r for practical problems. However, recently established methods based on semidefinite programming and SOS decomposition allow very efficiently verifying Lyapunov inequalities of form (24)in the case where G, V, r are assumed to be polynomials(Ebenbauer and Allg¨ower, 2004). Certainly, in our case, functions G, V, and r are all polynomial. In this case, the differentiation index of the differential-algebraic system is known, therefore it is reasonable to choose m to be equal to the differentiation index (i.e., µ = 1) (Mojica-Nava et al., 2010). Therefore, µ = 1 may be chosen and if we try to prove global stability of the system (22), the following polynomial inequalities must be satisfied,
V(x) > 0
∀ V (x) P(x,s) ≤ //Q(s)//2ρ(x,s)
which implies that
for all x = (x, ˙ x, s) ∈ R2n. Note that if V is polynomial and positive definite, it implies that V is radially unbounded.
For illustration and clarity of exposition, consider the case when q = 1. Dissipation inequality is
∀ V (x)(f0(x)(1-s)+f1(x)s≤//s(1-s)//2ρ(x,s) (26)
Using SOS concepts, inequality (26) can be posed as follows. Find polynomial V(x) so that
V(x)-φ(x)≥0 es SOS
-∀ V (x)(∑qk=0fk(x,u)lk(s))+...
//Πqk=0 (s-k)//2ρ(x,s)≥0 es SOS (27)
polynomials V(x), r (x, s) and positive definite function j(x) can be computed using SOSTOOLS (Prajna et al.,).
Numerical example: switched system: Consider the switched system described by ˙ x = fi(x), x = [x1 x2]T , with

This system is considered to be a homogeneous switched system presented in stability analysis (Zhang et al., 2007). Polynomial equivalent representation is used to prove stability under arbitrary switching:
x.(t)=f0(1-s)+f1s
s∈Γ ={s∈R/Q(s)=s(s-1)=0
Using these polynomial matrices and equation (27), the following is obtained:
-δV/δxf0(1-s)+f1(s)+(s4-2s3+s2)λ(x,s)≥0
Using SOSTOOLS, a Lyapunov function of degree six is found, i.e.
V(x)= -0,0364x21+0,02x41-0,0082x42+0,0476x22...
-0,056x1x2+0,0113x21x22-0,064x1x32-0,0457x61
...-0,016x41x42+0,0034x62
which, through theorem 3.4, proves that the homogeneous nonlinear switched system reformulated as a polynomial DAE is stable.
Conclusions
This tutorial has presented SOS techniques as effective criteria for proving the non-negativity of multivariable polynomial functions. Although determining non-negativity of a function could be an NPhard problem, using SOS decomposition is an efficient method for solving this problem. Moreover, by means of the SOSTOOLS computational tool the problem can be simplified to (appropriately) use the SOS algorithm, taking into account the inherent numerical errors and high computational cost of this tool for relatively high order systems. Some SOS conditions are given for analysing rational systems with nonlinear controllers and switched systems using a polynomial approach based on stability analysis of nonlinear polynomial systems. The SOS techniques were used to consider the parameters´ variations and possible uncertainties as inequality constraints on the original systems. Moreover, from the methods used to solve the presented examples it can be seen that SOS techniques are a useful method for dealing with high order and complex systems.
References
Anjos, M., Burer, S., On handling free variables in interior-point methods for conic linear optimization., SIAM Journal on Optimization, 18(4), 2007, pp.1310-1325.
Burden, R., Faires, J. D., Numerical Analysis PWS, Boston, 1985.
Ebenbauer, C., Allgöwer, F., Computer-Aided Stability Analysis of Differential-Algebraic Equations., In Proceedings of the NOLCOS, 2004, pp. 1025-1030.
Ebenbauer, C., Allgöwer, F., Analysis and Design of Polynomial Control Systems Using Dissipation Inequalities and Sum of Squares., Computers & Chemical Engineering, 30 (10-12), 2006, pp. 1590- 1602.
Franze, G., Casavola, A., Famularo, D., Garone, E., An off-line MPC Strategy for Nonlinear Systems Based on SOS Programming., Nonlinear Model Predictive Control, LNCIS 384, 2009, pp. 491-499.
Khalil, H., Nonlinear Systems., Prentice Hall Upper Saddle River, NJ, 2002.
Mojica-Nava, E., Quijano, N., Rakoto- Ravalontsalama, N., Gauthier, A., A Polynomial Approach to Stability Analysis of Switched Systems., Systems and Control Letters, 59(2), 2010, pp. 98-104.
Pantoja, A., Quijano, N., Modeling and Analysis for a Temperature System Based on Resource Dynamics and the Ideal Free Distribution., In Proceedings of the American Control Conference, 2008, pp. 3390-3395.
Papachristodoulou, A., Analysis of Nonlinear Time- Delay Systems Using the Sum of Squares Decomposition., In Proceedings of the American Control Conference, 2004, pp. 4153-4158.
Papachristodoulou, A., Prajna, S., On the Construction of Lyapunov Functions Using the Sum of Squares Decomposition., In Proceedings of the 41st IEEE Conference on Decision and Control, 2002, pp. 3482-3487.
Parrilo, P., Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization., Ph.D. thesis, California Institute of Technology, 2000.
Parrilo, P., Semidefinite Programming Relaxations for Semialgebraic Problems., Mathematical Programming, 96(2), 2003, pp. 293-320.
Prajna, S., Papachristodoulou, A., Parrilo, P., SOSTOOLS: Sum of Squares Optimization Toolbox for MATLAB-User Guide., Control and Dynamical Systems, California Institute of Technology, Pasadena, CA, 91125. Available on http://www.cds.caltech.edu/sostools.
Prajna, S., Papachristodoulou, A., Seiler, P., Parrilo, P., SOSTOOLS: Control Applications and New Developments., In Proceedings of the IEEE International Symposium on Computer Aided Control Systems Design, 2004, pp. 315-320.
Reznick, B., Some Concrete Aspects of Hilberts 17th Problem., Contemporary Mathematics, 253, 2000, pp. 251-272.
Topcu, U., Packard, A., Local Stability Analysis for Uncertain Nonlinear Systems., IEEE Transactions on Automatic Control, 54(5), 2009, pp. 1042-1047.
Topcu, U., Packard, A., Seiler, P., Local Stability Analysis Using Simulations and Sum-of-SquaresProgramming,, Automatica, 44(10), 2008, pp. 2669- 2675.
Zhang, L., Liu, S., Lan, H., On Stability of Switched Homogeneous Nonlinear Systems., J. Math. Anal. Appl, 334, 2007, pp. 414-430.
Zhao, J., Hill, D., Passivity and Stability of Switched Systems: A Multiple Storage Function Method., Systems & Control Letters, 57, 2008, pp. 158- 164.
References
Anjos, M., Burer, S., On handling free variables in interior-point methods for conic linear optimization., SIAM Journal on Optimization, 18(4), 2007, pp.1310-1325. DOI: https://doi.org/10.1137/06066847X
Burden, R., Faires, J. D., Numerical Analysis PWS, Boston, 1985.
Ebenbauer, C., Allgöwer, F., Computer-Aided Stability Analysis of Differential-Algebraic Equations., In Proceedings of the NOLCOS, 2004, pp. 1025-1030.
Ebenbauer, C., Allgöwer, F., Analysis and Design of Polynomial Control Systems Using Dissipation Inequalities and Sum of Squares., Computers & Chemical Engineering, 30 (10-12), 2006, pp. 1590- 1602. DOI: https://doi.org/10.1016/j.compchemeng.2006.05.014
Franze, G., Casavola, A., Famularo, D., Garone, E., An off-line MPC Strategy for Nonlinear Systems Based on SOS Programming., Nonlinear Model Predictive Control, LNCIS 384, 2009, pp. 491-499. DOI: https://doi.org/10.1007/978-3-642-01094-1_39
Khalil, H., Nonlinear Systems., Prentice Hall Upper Saddle River, NJ, 2002.
Mojica-Nava, E., Quijano, N., Rakoto- Ravalontsalama, N., Gauthier, A., A Polynomial Approach to Stability Analysis of Switched Systems., Systems and Control Letters, 59(2), 2010, pp. 98-104. DOI: https://doi.org/10.1016/j.sysconle.2009.12.004
Pantoja, A., Quijano, N., Modeling and Analysis for a Temperature System Based on Resource Dynamics and the Ideal Free Distribution., In Proceedings of the American Control Conference, 2008, pp. 3390-3395. DOI: https://doi.org/10.1109/ACC.2008.4587016
Papachristodoulou, A., Analysis of Nonlinear Time- Delay Systems Using the Sum of Squares Decomposition., In Proceedings of the American Control Conference, 2004, pp. 4153-4158. DOI: https://doi.org/10.23919/ACC.2004.1383959
Papachristodoulou, A., Prajna, S., On the Construction of Lyapunov Functions Using the Sum of Squares Decomposition., In Proceedings of the 41st IEEE Conference on Decision and Control, 2002, pp. 3482-3487.
Parrilo, P., Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization., Ph.D. thesis, California Institute of Technology, 2000.
Parrilo, P., Semidefinite Programming Relaxations for Semialgebraic Problems., Mathematical Programming, 96(2), 2003, pp. 293-320. DOI: https://doi.org/10.1007/s10107-003-0387-5
Prajna, S., Papachristodoulou, A., Parrilo, P., SOSTOOLS: Sum of Squares Optimization Toolbox for MATLAB-User Guide., Control and Dynamical Systems, California Institute of Technology, Pasadena, CA, 91125. Available on http://www.cds.caltech.edu/sostools.
Prajna, S., Papachristodoulou, A., Seiler, P., Parrilo, P., SOSTOOLS: Control Applications and New Developments., In Proceedings of the IEEE International Symposium on Computer Aided Control Systems Design, 2004, pp. 315-320.
Reznick, B., Some Concrete Aspects of Hilberts 17th Problem., Contemporary Mathematics, 253, 2000, pp. 251-272. DOI: https://doi.org/10.1090/conm/253/03936
Topcu, U., Packard, A., Local Stability Analysis for Uncertain Nonlinear Systems., IEEE Transactions on Automatic Control, 54(5), 2009, pp. 1042-1047. DOI: https://doi.org/10.1109/TAC.2009.2017157
Topcu, U., Packard, A., Seiler, P., Local Stability Analysis Using Simulations and Sum-of-Squares-Programming, Automatica, 44(10), 2008, pp. 2669- 2675. DOI: https://doi.org/10.1016/j.automatica.2008.03.010
Zhang, L., Liu, S., Lan, H., On Stability of Switched Homogeneous Nonlinear Systems., J. Math. Anal. Appl, 334, 2007, pp. 414-430. DOI: https://doi.org/10.1016/j.jmaa.2006.12.065
Zhao, J., Hill, D., Passivity and Stability of Switched Systems: A Multiple Storage Function Method., Systems & Control Letters, 57, 2008, pp. 158- 164. DOI: https://doi.org/10.1016/j.sysconle.2007.08.011
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
License
Copyright (c) 2010 Andrés Pantoja, Eduardo Mojica Nava, Nicanor Quijano

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors or holders of the copyright for each article hereby confer exclusive, limited and free authorization on the Universidad Nacional de Colombia's journal Ingeniería e Investigación concerning the aforementioned article which, once it has been evaluated and approved, will be submitted for publication, in line with the following items:
1. The version which has been corrected according to the evaluators' suggestions will be remitted and it will be made clear whether the aforementioned article is an unedited document regarding which the rights to be authorized are held and total responsibility will be assumed by the authors for the content of the work being submitted to Ingeniería e Investigación, the Universidad Nacional de Colombia and third-parties;
2. The authorization conferred on the journal will come into force from the date on which it is included in the respective volume and issue of Ingeniería e Investigación in the Open Journal Systems and on the journal's main page (https://revistas.unal.edu.co/index.php/ingeinv), as well as in different databases and indices in which the publication is indexed;
3. The authors authorize the Universidad Nacional de Colombia's journal Ingeniería e Investigación to publish the document in whatever required format (printed, digital, electronic or whatsoever known or yet to be discovered form) and authorize Ingeniería e Investigación to include the work in any indices and/or search engines deemed necessary for promoting its diffusion;
4. The authors accept that such authorization is given free of charge and they, therefore, waive any right to receive remuneration from the publication, distribution, public communication and any use whatsoever referred to in the terms of this authorization.



























