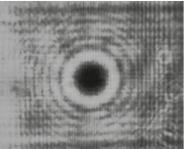
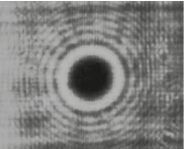
Superposition of two optical vortices with opposite integer or non-integer orbital angular momentum
Superposición de dos vórtices ópticos opuestos con momento angular orbital entero o no entero
DOI:
https://doi.org/10.15446/ing.investig.v36n1.43948Keywords:
Optical vortices, superposition, topological charge, orbital angular momentum. (en)Vórtices ópticos, superposición, carga topológica, momento angular orbital. (es)
This work develops a brief proposal to achieve the superposition of two opposite vortex beams, both with integer or non-integer mean value of the orbital angular momentum. The first part is about the generation of this kind of spatial light distributions through a modified Brown and Lohmann’s hologram. The inclusion of a simple mathematical expression into the pixelated grid’s transmittance function, based in Fourier domain properties, shifts the diffraction orders counterclockwise and clockwise to the same point and allows the addition of different modes. The strategy is theoretically and experimentally validated for the case of two opposite rotation helical wavefronts.
El presente trabajo desarrolla una breve propuesta para superponer dos vórtices ópticos con valor promedio de momento angular orbital entero de sentidos opuestos. En primera instancia se aborda la generación de éste tipo de distribuciones espaciales de luz a través del holograma modificado de Brown y Lohmann. Posteriormente se inserta un sencillo artificio matemático sobre la función de transmitancia de la rejilla pixelada basado en las propiedades del espacio de Fourier, para lograr desplazar los órdenes de difracción de sentidos levógiro y dextrógiro a un mismo punto espacial y efectuar la suma de los modos. Se valida la estrategia de manera teórico experimental para el caso de los dos frentes de onda helicoidales opuestos en rotación.
Superposition of two optical vortices with opposite
integer or non-integer orbital angular momentum
Superposición de dos vórtices ópticos opuestos
con momento angular orbital entero o no entero
C. F. Díaz1, Y. Torres2, and C. H. Acevedo3
1Carlos Fernando Díaz Meza: Electronic Engineer, Universidad Industrial de Santander, Colombia. Master in Electronic Engineer, Universidad Industrial de Santander, Colombia. Affiliation: Researcher, Universidad Industrial de Santander, Colombia. E-mail: marck177@hotmail.com.
2Yezid Torres Moreno: Physicist, Universidad Industrial de Santander, Colombia. PhD Optique Et Traitment Du Signal, Université de Franche Comté, France. Affiliation: Titular Professor, Universidad Industrial de Santander, Colombia. E-mail: ytorres@uis.edu.co.
3Cristian Hernando Acevedo Caceres: Physicist, Universidad Industrial de Santander, Colombia. Phd(c) Natural Sciences Physics, Universidad Industrial de Santander, Colombia. Affiliation: Catedra Professor, Universidad Industrial de Santander, Colombia. E-mail: cristian_rvd@yahoo.com.
How to cite: Díaz, C. F., Torres, Y., & Acevedo, C. H. (2016). Superposition of two optical vortices with opposite integer or non-integer orbital angular momentum. Ingeniería e Investigación, 36(1), 79-84.
DOI: https://doi.org/10.15446/ing.investig.v36n1.43948.
ABSTRACT
This work develops a brief proposal to achieve the superposition of two opposite vortex beams, both with integer or non-integer mean value of the orbital angular momentum. The first part is about the generation of this kind of spatial light distributions through a modified Brown and Lohmann’s hologram. The inclusion of a simple mathematical expression into the pixelated grid’s transmittance function, based in Fourier domain properties, shifts the diffraction orders counterclockwise and clockwise to the same point and allows the addition of different modes. The strategy is theoretically and experimentally validated for the case of two opposite rotation helical wavefronts.
Keywords: Optical vortices, superposition, topological charge, orbital angular momentum.
RESUMEN
El presente trabajo desarrolla una breve propuesta para superponer dos vórtices ópticos con valor promedio de momento angular orbital entero de sentidos opuestos. En primera instancia se aborda la generación de éste tipo de distribuciones espaciales de luz a través del holograma modificado de Brown y Lohmann. Posteriormente se inserta un sencillo artificio matemático sobre la función de transmitancia de la rejilla pixelada basado en las propiedades del espacio de Fourier, para lograr desplazar los órdenes de difracción de sentidos levógiro y dextrógiro a un mismo punto espacial y efectuar la suma de los modos. Se valida la estrategia de manera teórico experimental para el caso de los dos frentes de onda helicoidales opuestos en rotación.
Palabras clave: Vórtices ópticos, superposición, carga topológica, momento angular orbital.
Received: June 9th 2014
Accepted: October 8th 2015
Introduction
Since Allen et al. (1992) explicitly demonstrated that light carries orbital angular momentum (OAM), and spin angular momentum (SAM), various methodologies have been proposed and developed to produce beams with this rotational dynamic in the wavefront.
Astigmatic converters, phase plates (Beijersbergen et al., 1993, 1994) and computer-generated holograms (CGH) (Heckenberg, 1992; Janicijevic, 2008) are the techniques most often used to generate optical vortices with topological charge (TC) and therefore a beam with well defined OAM. However, based on the Díaz et al. (2012) review, CHG are selected as the most simple and feasible method to be implemented in a hybrid system, by the variety of modes that are generated and availability of equipment in the optics laboratory in Universidad Industrial de Santander (Bucaramanga/Colombia) for this kind of setup.
This optoelectronic system comprises a coherent light source of 532 nm wavelength, a collimator, one spatial light modulator (SLM), two computers and a CCD camera to record the intensity of the light.
The CGH that deploys over the SLM is a modified transmittance function; the original was exposed in the late sixties by Brown and Lohmann (1969). It allows to incorporate the azimuthal phase term on the diffraction orders of the incident beam, producing optical vortices with mean value of OAM both integer and fractional (Gotte et al., 2007, Berry et al., 2004).
The superposition of this kind spatial light distributions, requires the inclusion of other types of arrangements in the original architecture such as porro prisms, mirror-mirror systems or circulars grids (Naidoo et al., 2011, 2012; Dudley, 2012), which attenuates the beams intensity and increases the number and length of optical paths for the mode to be propagated.
Below, a simple proposal to add wavefronts with a specified integer or non-integer mean value of the OAM is discussed. From the signal processing point of view, the modes superposition is made with a single propagation path and without additional hardware.
Optical vortices generation
All beams whose spatial light configuration is multiplied by an azimuthal phase term 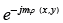 have a wavefront with helical pattern and an optic vortex in the intensity, with a radius that varies according to the m value related with the OAM.
have a wavefront with helical pattern and an optic vortex in the intensity, with a radius that varies according to the m value related with the OAM.
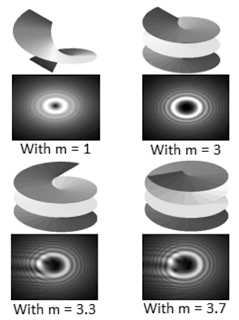
Figure 1. Helical structure and intensity patterns with Bessel Gauss envelope and different values of m.
The phase singularity is inserted on a Gaussian plane wavefront beam, were it is transmitted by a set of CGH displayed in a translucent matrix Holoeye, LC2002 model. The far field is composed of the different diffraction orders, each one with an optical vortex with different OAM mean value. The centered order at the optical axis has a null OAM and the vortices placed on the right and left sides are symmetrical with opposite signs.
However, there are various pixelated grids for that purpose. The Brown and Lohmann’s blazed CGH (1969) Equation (1) adapts a specific angle for raising diffraction efficiency as much as possible, modifying the interfringe step d on the transmittance function T(x,y), with n equal to the number of orders to propagate.
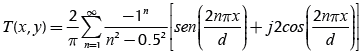 (1)
(1)
The mathematical description above does not include an azimuthal mask. This transmittance function is unable to produce an optical vortex, and therefore a variant T1(x,y) in Equation (2) is proposed, inserting a phase singularity (3) with the step index m.
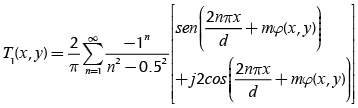 (2)
(2)
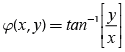 (3)
(3)
The hologram from T1(x,y) presented in Figure 2 produces two optical vortices in the Fresnel-Fraunhofer space. The related simulations in Figures 3 and 4 are corresponding to the vortex profiles exposed by Leach (2004).

Figure 2. CGH generated from the new function with step index m = +5.
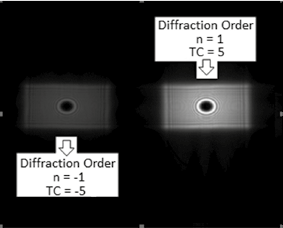
Figure 3. Optical vortices propagated with m = −5 (left) and m = +5 (right).
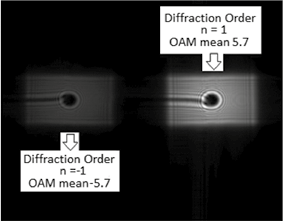
Figure 4. Optical vortices propagated with OAM mean −5,7 (left) and +5,7 (right).
The related signs of azimuthal index in the resulting spatial distribution of light indicate the direction of counterclockwise or clockwise rotation of the diffracted components (G. Gibson et al., 2004). The wavefront of each of the orders propagates with the same helical periodicity but opposite orientation.
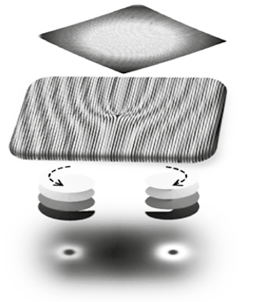
Figure 5. Diffracted optical vortices with opposite orientation generated from incidence of fundamental mode on CGH.
Some experimental results over the privileged diffraction order by the CGH are:
|
|
|
|
TC. m = 1 |
TC. m = 2 |
|
|
|
|
TC. m = 4 |
TC. m = 5 |
|
|
|
|
OAM mean 5.1 |
OAM mean 5.2 |
|
|
|
|
OAM mean 5.8 |
OAM mean 5.9 |
Figure 6. Optical vortices with different TC (first four images) and different OAM mean (last four images).
Superposition of two optical vortices with opposite OAMs.
The process of superposition is mainly based in the use of two wavefronts generated with the physics property of interest, with the counterclockwise and clockwise rotation that is present in the far field.
The idea is movethe two spatial light configurations to the same propagation axis in the reciprocal space and without inserting other optical components. This is possible if these modes are convolved with two pulses located at the same point where the vorticess are placed.
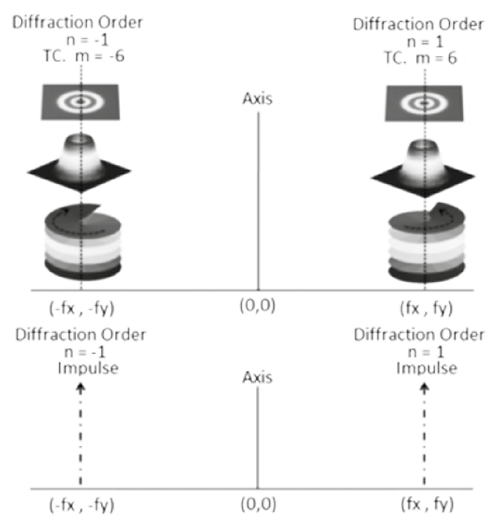
Figure 7. Modes (above) and impulses (below) located in far field.
Refer to the Figure 7 for the particular case of superposition of two opposite rotation modes; the convolution between the impulse located in (−fy, −fx) and the vortex in (fy, fx), shift this to the optical axis. The same effect occurs with the convolution between the Dirac pulse placed in (fy, fx) and the beam centered at (−fy, −fx), as shown in Figure 8.
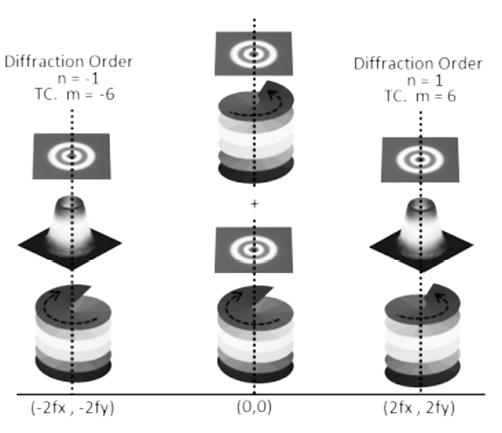
Figure 8. Modes and impulses located in far field.
Mathematically, in order to locate these Dirac pulses in the corresponding inverse space, multiply the transmittance function T1(x,y) by the cosine expression in the direct space; see Equation (4). This operation is equivalent to the inverse Fourier transform of two symmetrically shifted deltas Dirac distribution.
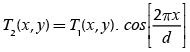 (4)
(4)
The resultant field due to superposition the opposite modes is expressed as:
 (5)
(5)
where A1(x,y,z) describes any kind of spatial light distribution: Laguerre Gauss, Bessel, Airy, Mathieu, plane, among others. The azimuthal phase terms 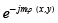 and
and  correspond to the wavefront dislocations.
correspond to the wavefront dislocations.
The intensity of the two overlapped diffraction orders is written as:
 (6)
(6)
From the last expression, it can be observed that resulting spatial light configuration must exhibit a number of constructive and destructive interference that is equal to twice the value of the TC of the modified CGH T2(x,y).
The theoretical and experimental results for the superposition of opposite modes with TC are presented below:

Figure 9. Simulation of the intensity profile of the diffraction orders superposition with m = −2 and m = +2.

Figure 10. Simulation of the intensity profile of the diffraction orders superposition with m = −3 and m = +3.

Figure 11. Simulation of the intensity profile of the diffraction orders superposition with m = −4 and m = +4.

Figure 12. Simulation of the intensity profile of the diffraction orders superposition with m = −5 and m = +5.
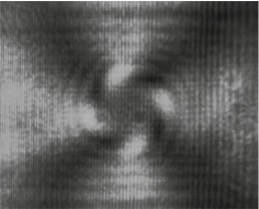
Figure 13. Experimental intensity profile of the diffraction orders superposition with m = −2 and m = +2.
When extending the procedure described for optical vortices with non-integer OAM mean is obtained the next profiles.

Figure 14. Experimental intensity profile of the diffraction orders superposition with m = −3 and m = +3.

Figure 15. Experimental intensity profile of the diffraction orders superposition with m = −4 and m = +4.

Figure 16. Experimental intensity profile of the diffraction orders superposition with m = −5 and m = +5.
|
|
|
|
Superposition with opposite rotation, modes with m = + 5 and m = − 5. |
Superposition with opposite rotation, modes with m = + 5.1 and m = − 5.1. |
|
|
|
|
Superposition with opposite rotation, |
Superposition with opposite rotation, modes with m = + 5.3 and m = − 5.3. |
|
|
|
|
Superposition with opposite rotation, modes with m = + 5.4 and m = − 5.4. |
Superposition with opposite rotation, modes with m = + 5.5 and m = − 5.5. |
|
|
|
|
Superposition with opposite rotation, modes with m = + 5.6 and m = − 5.6. |
Superposition with opposite rotation, modes with m = + 5.7 and m = − 5.7. |
|
|
|
|
Superposition with opposite rotation, modes with m = + 5.8 and m = − 5.8. |
Superposition with opposite rotation, modes with m = + 5.9 and m = − 5.9. |
|
|
|
|
Superposition with opposite rotation, |
|
Figure 17. Experimental intensity profiles of the superposition of the diffraction orders for TC X and X, with OAM mean values of 0.1 steps
Note the images presented in the Figure 17, as they generate additional interference with the increasing of the OAM mean values superposed, associated to phase dislocations, with steps of 0.1.
The first fringe begins to be generated at the left side of the image for the OAM mean superposed of 5.1, and it is consolidated at an OAM mean superposed of 5.3. The second and necessary additional interference fringe begins to be generated in the same place that the first one, at the left side of the image for the OAM mean superposed of 5.7, and is consolidated at a 5.9 OAM mean superposed value.
Conclusions and observations
The transmittance function T1(x, y) spreads the wavefronts with the respective phase dislocations inserted by the phase step index of the CGH. The privileged diffraction order can be selected interchanged the imaginary factor that multiply sinusoidal expression in the Equation (2).
The number of destructive and constructive interferences for both results, from the numerical simulation and from the experiment, validates the procedure of modulation for the CGH, using the new proposed transmittance function T2(x, y)as an option to superpose vortices with TC or non-integer OAM mean with opposite rotation.
With this proposed technique it is possible to generate both even and odd numbers of constructive and destructive interferences, along the azimuthal direction of the spatial light distribution produced by the superposed vortex beams.
The work answers a remaining question about the place of origin of the new interference fringes when opposite sign non-integer OAM mean modes are superposed. The experimental results confirm that this place is the same spatial position where the discontinuity in the non-integer phase step index is written on the CGH. Rotation of the interference pattern is achieved changing the initial phase position for the modulated hologram deployed over the SLM.
Acknowledgements
The authors thank anonymous referees for their helpful suggestions. They also thank Universidad Industrial de Santander - UIS, for supporting this research by means of the Research and Services (VIE), with funding projects 5708 and 1788, both of the institutional program for consolidation of research groups, years 2013 and 2014, respectively.
Additionally, they thank Colciencias for their support in this research project, titled “Optics devices for quantum key distribution, high dimensionality systems based in orbital angular momentum of light”, number 110256934957, funding results from the National call for a bank of projects in science, technology and innovation 2012.
References
Allen, L., Beijersbergen, M., Spreeuw, R., & Woerdman, J.P. (1992). Orbital angular momentum of light and the transformation ofLaguerre Gaussian laser modes. Physical Review A, 45(11), 8185–8189. DOI: 10.1103/PhysRevA.45.8185.
Beijersbergen, M., Allen, L., van der Veen, H.E.L.O. & Woerdman, J.P. (1993). Astigmatic laser mode converters and transfer of orbital angular momentum. Optics Communications, 96(1), 123-132. DOI: 10.1016/0030-4018(93)90535-D.
Beijersbergen, M., Coerwinkel, R.P.C., Kristensen, M. & Woerdman, J.P. (1994). Helical wave-front laser beams produced with a spiral phase plate. Optics Communications, 112(5), 321-327. DOI: 10.1016/0030-4018(94)90638-6.
Berry, M.V. (2004). Optical vortices evolving from helicoidal integer and fractional phase steps. Journal of Optics A, 6(2), 259-268. DOI: 10.1088/1464-4258/6/2/018.
Brown, B., & Lohmann, A. (1969). Computer-generated binary holograms. IBM Journal of Research and Development, 13(2), 160-168. DOI: 10.1147/rd.132.0160.
Díaz, C., Torres, Y., Acevedo, C., & Barrero, J. (2012). Preliminary optoelectronic encoder modeling for data transfer through the orbital angular momentum of light. Revista UIS ingenierías, 11(1), 35-43.
Dudley, A. (2012). Superpositions of light fields carrying orbital angular momentum (Unpublished doctoral dissertation). University of Kwazulu-Natal, School of Chemistry and Physics, South Africa.
Gibson, G., Courtial, J., Padgett, M., Vasnetsov, M., Barnett, S., & Sonja Franke-Arnold. (2004). Free-space information transfer using light beams carrying orbital angular momentum. Optics Express, 12(22), 5448-5456. DOI: 10.1364/OPEX.12.005448.
Götte, J.B., Franke-Arnold, S., Zambrini, R., & Barnett, S.M. (2007). Quantum formulation of fractional orbital angular momentum. Journal of Modern Optics, 54, 1723-1738. DOI: 10.1080/09500340601156827.
Heckenberg, N. R., McDuff, R., Smith, C. P., & White, A. G. (1992). Generation of optical phase singularities by computer-generated holograms. Opt. Lett, 17(3), 221–223. DOI: 10.1364/OL.17.000221.
Janicijevic, L., & Topuzoski, S. (2008). Fresnel and Fraunhofer diffraction of a Gaussian laser beam by fork-shaped gratings. JOSA A, 25(11), 2659-2669. DOI: 10.1364/JOSAA.25.002659.
Leach, J., Yao, E., & Padgett, M.J. (2004). Observation of the vortex structure of a non-integer vortex beam. New J. Phys., 6(1), 71-78. DOI: 10.1088/1367-2630/6/1/071.
Naidoo, D., Aït-Ameur, K., Brunel, M., & Forbes, A. (2012). Intra-cavity generation of superpositions of Laguerre-Gaussian beams. J. of Appl. Phys. B: Lasers and Optics, 106(3), 683-690. DOI: 10.1007/s00340-011-4775-x.
Naidoo, D., Forbes, A., Ait-Ameur, K., & Brunel, M. (2011). Constructing petal modes from the coherent superposition of Laguerre-Gaussian modes. SPIE LASE, 791304-791304. DOI: 10.1117/12.876854.