New digital demodulator with matched filters and curve segmentation techniques for BFSK demodulation: FPGA implementation and results

Nuevo demodulador digital con filtros macheados y técnicas de segmentación de curvas para la demodulación de señales BFSK: Implementación en FPGA y resultados

The current article addresses digital implementation of new demodulation schemes for Binary Frequency Shift Keying (BFSK), and has two main objectives: of the description of the performance of the new processing method and its implementation on FPGA technology. Performance is analyzed by means of the total number of demodulated bits free of errors without noise, and by means of the BER parameter. The proposed method exhibits to have better performance than the solutions reported. Additionally, the solution obtained shows lower complexity than reported methods in regard to the total number of adders and multipliers. The implementation is described for FPGA systems, and the System Generator software is used for testing and simulating the results.

 

 

El presente artículo aborda la implementación digital de un nuevo esquema de demodulación para la modulación Binary Frequency Shift Keying (BFSK), y tiene dos objetivos principales: la descripción del desempeño del nuevo método, así como su implementación con la tecnología FPGA. El desempeño se analiza teniendo en cuenta el total de bits demodulados libre de errores en un ambiente sin ruido, y por medio del parámetro BER. El método propuesto exhibe un mejor desempeño en cuanto a estos parámetros en comparación con otras soluciones reportadas. Adicionalmente, la solución obtenida muestra menor complejidad que las reportadas en la literatura científica, teniendo en cuenta el total de sumadores y multiplicadores. La implementación del demodulador propuesto se desarrolla sobre un sistema FPGA, y con el empleo de la aplicación System Generator se obtienen los resultados de prueba y simulación.

J. Torre¹, F. Hernández², and J. Habermann³

---

¹Jorge Torres Gómez: BSc. in Telecommunications and Electronics, MSc. in Telecommunication Systems, PhD in Telecommunication Systems, Affiliation: Department of Telecommunications and Telematics, Electrical School, CUJAE, Cuba. Email: jorge.tg@electrica.cujae.edu.cu.

²Fidel Ernesto Hernández Montero: MSc in Digital Systems from CUJAE in 2000, PhD degree in Electronics and Industrial Automation from University of Mondragon, Spain, in 2006, Affiliation: Department of Telecommunications and Telematics, Electrical School, CUJAE, University of Pinar del Rio, Cuba. Email: alaina@tele.upr.edu.cu.

³Joachim Habermann: Dr.-Ing. (PhD) degrees in Electrical Engineering both with highest honors from the Technical University of Darmstadt, Germany. Senior member of the Institute of Electrical and Electronics Engineers (SM IEEE). reviewer of several research institutions, such as the German Research Council (DFG), Affiliation: full professor in the Department of Electrical Engineering and Information Technology of the Technische Hochschule Mittelhessen (THM), University of Applied SciencesGiessen, Germany. Email: joachim.habermann@iem.thm.de.

---

How to cite: Torres, J., Hernández, F., & Habermann, J. (2015). New digital demodulator with matched filters and curve segmentation techniques for BFSK demodulation: FPGA implementation and results. Ingeniería e Investigación, 36(1), 105-110. DOI: https://doi.org/10.15446/ing.investig.v36n1.47388.

---

ABSTRACT

Keywords: Curve segmentation, digital demodulation, BFSK, FPGA.

---

RESUMEN

Palabras clave: Segmentación de curvas, demodulación digital, BFSK, FPGA.

---

Received: November 20th 2014

Accepted: November 10th 2015

---

Introduction

Digital frequency modulations such as Frequency Shift Keying (FSK) are commonly applied in wireless technologies (Ibrahim, Hafez, & Khalil, 2013) (Peng, Lin, & Chao, 2013), satellite communications(VEŘTÁT & MRÁZ, 2013), power lines communications (PLC) (Ouahada, 2014), mobile communications (Karabulut, Ozdemir, & Ilhan, 2015), spread spectrum systems (Neifar, Trabelsi, Bouzid, & Masmoudi, 2012) and biomedical applications (Wang, Chen, Lin, & Lee, 2014). Among the reported demodulators, methods to demodulate Binary Frequency Shift Keying (FSK) signals with the aid of correlators are of particular interest in this paper. The most common solutions in this regard are the receivers based on a Quadricorrelator (Gardner, 1985), Balanced Quadricorrelator (Kang, Kim, & Park, 2011) and Quotient Detector (Kreuzgruber, 1994), all of these well known in scientific literature. However, these schemes are implemented by means of lowpass filters (LPF), which in turn demand a high complexity when higher order filters are applied.

On the other hand, a different solution can be obtained with the use of matched filters and curve segmentation techniques. This method is advantageous in the sense that it achieves a strong reduction in hardware complexity.

In this paper the implementation of the system is addressed and the applicability of the proposed solution with FPGA (Field Programmable Gate Array) technology is explained. Besides, an algorithm is required to be developed for recovering the bits transmitted. This symbol synchronization procedure allows to complete the demodulation process. In this paper, closed form expressions are obtained in order to describe the performance.

The rest of the paper is organized as follows: Section 2 summarizes the proposed receiver; Section 3 develops closed form expressions for recovering the binary data; in Section 4 the simulation results are shown and in Section 5 the implementation on a FPGA is described. Conclusions are presented in Section 6.

Non-coherent and asynchronous receiver

Figure 1 depicts the proposed scheme. The system is comprised of the discrete correlator and the detection blocks.

Figure 1. Receiver for the BFSK waveform with segmentation curve techniques.

The discrete correlator accumulates the multiplication result, followed by the curvatures measurement block for estimating the slope at its input. The slope estimation algorithm is performed by means of the relation:

(1)

where:

Given a BFSK signal at the system input, the output signal 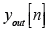is shown in Figure 2. In order to detect the binary levels, a value for the threshold is derived by means of:

(2)

where:

(3)

(4)

(5)

Figure 2. a) Upper part: Receiver input in Figure 1. b) Lower part: Output for the receiver in Figure 1 applying the k-angular bending segmentation curve algorithm. Parameters: ω₀ = 0,1425 rad/s, ω₁= 0,3562 rad/s, k = 44 samples.

The term Δ₁ describes the case where the frequency received is equal to the frequency of the local oscillator at the receiver. This term determines the amplitude of the oscillation at the output. The term Δ₀ describes the contrary case, that is, when the frequency received is different from the local tone generated.

The length of window k can be chosen in order to minimize the amplitude of the oscillations at the output given by Δ₀ and Δ₁. In this work, Δ₁ is cancelled by the following relation in order to become zero the term from (5):

(6)

The operations given in Equations (1) and (2) perform the signal processing steps of the proposed receiver. However, two issues of interest must be further discussed:

I. Symbol synchronization: The system depicted in Figure 1 recovers the binary levels from the waveform received as depicted in Figure 2. However, the bits transmitted must be extracted from the rectangular pulses in Figure 2 b) in order to recover the information. The synchronization of the pulses obtained in Figure 2 b) must be accomplished for that purpose (this is considered in Section 3).

II. Implementation: The algorithm has to be efficiently implemented with the state of the art FPGA devices.

Data Recovery

The recovery process of the binary levels from a BFSK waveform using the scheme in Figure 1 have been described in the previous Section. In this Section, the synchronization procedure is presented. This is useful in determining the bits transmitted, and completely describes the process of demodulation.

Once the high and low levels have been recovered, as indicated in Figure 2, the total amount of “1's” and “0's” in a transmitted data block for each level has to be obtained. The length in time of either a “1” or a “0” is given by the symbol time and is denoted as T_s. The comparison of the length of the level and T_s will result in the quantity of “1's” and “0's” under each level. However, this comparison is prone to errors since the transition of each level is not abrupt; in this case, there is an upper bound on the total of bits to be analyzed without error (error free). The present Section analyzes this situation giving closed form expressions.

The algorithm for data recovery is as follows:

• Sketching a histogram where the abscissa represents the length of a transition in samples; the amplitude is given by the number of occurrences of these lengths. An example is given in Figure 3 b), where the abscissa represents the duration of the interval in a). This histogram is used for the estimation of the symbol duration.
• The histogram is comprised of peaks as indicated in Figure 3 b), where the peak closer to zero is related to the symbol duration, leading to the estimation of T_s as indicated in Figure 3 c). The estimation of T_s is obtained as:

(7)

where N₁ and N₂ represent the intervals of the x-axis (e.g. N₁ = 200 and N₂ = 250 in Figure 3c), in that portion of the histogram with values unequal to zero, T_m represents the sample period, and h [i] represents the values at specific time instants.

The length of the high levels in Figure 3 are established by the intersection of the output signal of the system with the threshold y_th of (2). In this case, the length of these measures are modified from symbol to symbol because of the smooth transitions between levels. The accuracy in the determination of T_s, denoted by Δt, could be estimated by calculating the deviation, as indicated in Figure 3 c) through the following relation:

(8)

Once is obtained, the transmitted digital information is recovered by dividing the length of each level, obtained by the interceptions between the output of the system and the threshold y_th, with the symbol time. The total of bits represented is recovered by rounding the result to the nearest integer.

The accuracy to be obtained on the third step depends on the deviation Δt. If b identical symbols are supposed to be transmitted sequentially, then the level duration at the output of Figure 1 can be approximated by b • T_s plus the deviation, i.e. the square root of the variance Δt. If this resulting duration is divided by T_s+ Δt, then the total bits to be recovered can be described by the following approximate expression, using Laurant expansion and considering :

(9)

Expression (8) utilizes the addition of the variance to the symbol time instead of substraction because the linear components in the system of Figure 1 tend to expand the transitions and not to contract. Besides, the same variance is also considered on each transition as a simplification in the determination of accuracy. This considers that the system responds in the same way, no matter the total symbols received.

Figure 3. Details regarding the transition between consecutive symbols. a) Signal received and binary levels. b) Histogram of the length of transitions. c) Horizontal Zoom of b).

An error in the estimation of b occurs when the second term in Equation (8) is larger than 0.5. In such a case, the estimated value will be larger than when the correct value is b. Hence, even in the absence of noise the estimation of consecutive symbols is limited in order to perform an error free reception.

Equation (8) represents the upper bound for k when T_s and Δt are substituted by and respectively, since both values are obtained via the histogram. This equation gives an idea on how many bits the system in Figure 1 might be receiving without errors in the absence of noise. The probability of transmitting k bits comprised of repetitive sequences of “1's” and “0's” is , so an error could happen once in 2^b-1transmitted bits. This is why the receiver is upper bounded in the total number of bits to be processed. The following relation is a closed form expression that represents a figure of merit for the receivers analyzed, and its values are analyzed in the next Section:

(10)

Results

The proposed solution is analyzed taking into account the precision by means of (9) and the BER (Bit Error Rate) curves are obtained with the aid of simulations.

Precision

Numerical simulations were done in order to compare the proposed receiver with that of the Balanced Quadricorrelator. Experiments were performed using m = 10, ω₀= 0.3562 [rad/s] and ω₁= 0.1425 [rad/s], and results yielded a precision (given by Equation (9)) of 61 for the proposed solution, and 1175 for the Balanced Quadricorrelator. Although the Balanced Quadricorrelator exhibits a higher precision than the proposed solution, the proposed receiver can also be employed if a sequence of 61 or less all-one or all-zero bits are transmitted. Considering the probability of occurrence of this case, a total of 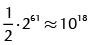bits can be transmitted free of errors in the absence of noise, which represents a useful value for establishing a communication link.

Performance in noise

Figure 4 depicts the measured BER as a function of the signal to noise ratio (SNR) in comparison to the Balanced Quadricorrelator. The parameters employed were ω₀= 0.3562 [rad/s] and ω₁= 0.1425 [rad/s], m = 6 and k = 6 samples. The simulation was performed using a total number of 106 bits in steps of 0.25 dB on the SNR axis. The range analyzed is below an SNR equal to 5 dB, since up to this value error correcting codes are usually employed (Carlson, Crilly, & Rutledge, 2002).

Figure 4. Bit error rate performance.

The BER performance of the proposed solution is worse than the Balanced Quadricorrelator. This is due to the fact that the proposed method does not use lowpass filters (LPF) like the Balanced Quadricorrelator; the system depicted in Figure 1 is mainly based on accumulators. However, if a LPF is employed at the output of the system, as shown in Figure 5, with the same bandwidth as the Balanced Quadricorrelator, then a better performance is obtained, as depicted in Figure 4.

Figure 5. Proposed receiver with a lowpass filter at the output.

Hardware Implementation.

This Section describes a generic design without specifying the FPGA employed. The design is investigated with the aid of simulations by means of the System Generator Software for Xilinx.

The discrete correlator, , from Figure 1 is implemented by a first order IIR filter, as shown in Figure 6. The cosine function and the BFSK waveform are fed into the system through mat files in Matlab®.

The block for the curvature measurement is implemented using the relation (1). This relation performs an operation similar to a FIR filter as indicated by:

(11)

where the impulse response sequence h[n] is equal to the unite vector, and the input x[n] is fed by the sequence . The digital implementation of this procedure can be developed with a delay block and a FIR filter with all its coefficients set to one.

Figure 6 shows the details for the discrete correlator and the curvature measurement block. The implementation of the curvature measurement block does not consider the constant c in the system. This constant can be simply incorporated in the detection by just multiplying the output by c2 or dividing the threshold by the same quantity.

Figure 6. System Implemented on the System Generator Software.

Figure 7 depicts the entire system in the System Generator Environment, and Figure 8 shows the results. It can be observed that high and low levels are obtained in accordance with the received symbols.

The receiver depicted in Figure 7 is built without the use of digital filters. The complex elements are realized by accumulator blocks. On the other hand, the Balanced Quadricorrelator is implemented with two lowpass filters and two time-discrete differentiators, and this system demands more digital adders and multipliers when the order of the filters is high. In this regard, the proposed solution shows a reduction in hardware complexity.

Figure 7. Implemented System on the System Generator Software.

Figure 8. Results obtained from the simulation of the system in the System Generator Software. Parameters: ω0 = 0.3562 [rad/s]], ω1= 0.1425 [rad/s], k = 72 samples.

The implementation of systems on FPGA technology is useful for several reasons. It allows the parallel implementation of several modules, that is, the receiver in Figure 6 can be duplicated in order to demodulate on a different band at the same time. Although the solution can be implemented on serial processors like a microcontroller, this lacks of multiband operation, and it is commonly demanded in applications for communications. On the other hand, FPGA technology implements digital hardware with the advantages of stability, flexibility and reliable reproduction in comparison with the analogic implementations (Carlson et al., 2002).

Conclusions

In this paper the performance and the implementation of a new digital receiver is analyzed. The main advantage of the proposed solution is the low complexity, achieved by avoiding the use of higher order filters. The system is merely based on accumulators, devices suitable for low complexity FPGA implementation.

Although the precision obtained is worse than the Balanced Quadricorrelator, the value achieved is sufficient for establishing communications. In order to reduce the effect of noise, and additional lowpass filter can be inserted to improve the performance. This solution is still less complex in hardware than the Balanced Quadricorrelator, which makes use of an additional LPF.

References

Carlson, A. B., Crilly, P. B., & Rutledge, J. C. (2002). Communication Systems: An introduction to Signals and Noise in Electrical Communication (Fourth Edition). New York, NY, USA: McGraw-Hill.

Gardner, F. (1985). Properties of Frequency Difference Detectors. IEEE Transactions on Communications, 33(2), 131 – 138. DOI: 10.1109/TCOM.1985.1096264.

Ibrahim, G. H., Hafez, A., & Khalil, A. H. (2013). An ultra low power QPSK receiver based on super-regenerative oscillator with a novel digital phase detection technique. AEU - International Journal of Electronics and Communications, 67(11), 967–974. DOI: 10.1016/j.aeue.2013.05.008.

Kang, H.-S., Kim, D., & Park, S.-C. (2011). Coarse frequency offset estimation using a delayed auto-quadricorrelator in OFDM-based WLANs. In 2011 3rd International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT) (pp. 1–4). Budapest, Hungary.

Karabulut, M. A., Ozdemir, O., & Ilhan, H. (2015). Link adaptive relaying with noncoherent BFSK and DPSK modulations in multiple access relay channels. In Wireless Telecommunications Symposium (WTS), 2015 (pp. 1–5) DOI: http://doi.org/10.1109/WTS.2015.7117265.

Kreuzgruber, P. (1994). A class of binary FSK direct conversion receivers. In Vehicular Technology Conference, 1994 IEEE 44th (pp. 457 –461 vol.1). http://doi.org/10.1109/VETEC.1994.345086.

Neifar, A., Trabelsi, H., Bouzid, G., & Masmoudi, M. (2012). Design of a zero crossing BFSK demodulator for a wireless sensor. In 2012 7th International Conference on Design Technology of Integrated Systems in Nanoscale Era (DTIS) (pp. 1–5).DOI: 10.1109/DTIS.2012.6232953.

Ouahada, K. (2014). Nonbinary convolutional codes and modified M-FSK detectors for power-line communications channel. Journal of Communications and Networks, 16(3), 270–279. DOI: 10.1109/JCN.2014.000047.

Peng, K.-C., Lin, C.-C., & Chao, C.-H. (2013). A Novel Three-Point Modulation Technique for Fractional-N Frequency Synthesizer Applications. Radioengineering, 22(1), 269–275.

VEŘTÁT, I., & MRÁZ, J. (2013). Hybrid M-FSK/DQPSK Modulations for CubeSat Picosatellites. Radioengineering, 22(1), 389–393.

Wang, L.-H., Chen, T.-Y., Lin, K.-H., & Lee, S.-Y. (2014). A low-power super-regenerative BFSK transceiver for intelligent healthcare monitoring system. In 2014 IEEE International Symposium on Bioelectronics and Bioinformatics (ISBB) (pp. 1–4). DOI: 10.1109/ISBB.2014.6820913.