Influence of heat transfer on two-phase flow behavior in onshore oil pipelines
Influencia de la transferencia de calor en el comportamiento de un flujo bifásico en ductos terrestres de petróleo
DOI:
https://doi.org/10.15446/ing.investig.v36n1.51570Keywords:
Heat exchange, oil pipeline, two-phase flow, pressure drop, Pipesim. (en)Intercambio de calor, tubería de petróleo, flujo bifásico, disminución de presión, Pipesim. (es)
Computational tools for simulation of multiphase flow in oil pipelines are of great importance for the determination of the technical feasibility of the production in oilfields. The present article presents the mathematical and numerical modeling of the oil biphasic flow in a partially submerged onshore pipeline. The biphasic behavior of the heavy oil of 13,2ºAPI is translated by the Dukler correlation. The oil’s viscosity is regarded as dependent on the temperature and on the API density of the oil by means of the Hossain correlation. The pipeline, of 3,600m and 4 inches (10.16cm) in diameter, transports the oil from a collecting station to a storage center and consists of three sections. The first and third sections are above ground and are in contact with the external environment. The intermediate section is sitting on the river bed and is the critical part of the pipeline, once high heat losses are observed. The influence on the type of pipe insulation in the pressure and temperature gradients was analyzed with the aid of commercial 1D software Pipesim®. The results, of this 1D and non-isothermal problem with prescribed outlet pressure, show that the use of isolation when appropriately designed in terms of material quality and thickness is of utmost importance to maintain the heat transfer at low levels, in order to ensure the movement of fluids in long sections without compromising the system operation.
Las herramientas computacionales para la simulación numérica del flujo bifásico en tuberías son importantes para determinar la viabilidad técnica de producción de campos de petróleo. En este artículo se presenta el modelamiento matemático y numérico del flujo bifásico en una tubería terrestre parcialmente inmersa en un río. La correlación de Dukler es utilizada para modelar la presencia de más de una fases de fluidos. La dependencia de la viscosidad con la temperatura y el grado API del petróleo siendo transportado es introducida por la correlación de Hossain. La tubería transporta petróleo desde una estación de colecta (que recibe la producción de varios pozos) hasta un centro de almacenamiento. Esta tubería, de 3600m y 4 pulgadas de diámetro, es formada por tres secciones. La primera y tercera se apoyan directamente sobre el suelo, intercambiando calor con el aire externo. La segunda sección pasa por el lecho de un río, estando expuesta a un intercambio de calor más intenso. La tubería es aislada en toda su extensión y la influencia del tipo de material del aislamiento que la recubre, así como la utilización de una bomba para impulsar el fluido, es estudiado mediante el software unidimensional Pipesim® para condición de presión prescrita en la salida. Los resultados obtenidos para el problema no isotérmico muestran que el tipo de aislamiento es muy importante para garantizar que el intercambio de calor entre el petróleo caliente y el medio externo más frío permanezca en niveles adecuados, de forma a que el transporte de fluidos en las secciones extensas de la tubería no comprometan la operación del sistema.
Influence of heat transfer on two-phase flow
behavior in onshore oil pipelines
Influencia de la transferencia de calor en el comportamiento
de un flujo bifásico en ductos terrestres de petróleo
O. J. Romero1, H. C. Saad2, I. B. Pereira3, and M. I. Romero4
1Oldrich Joel Romero. D. Sc. PUC-Rio, Brazil. Affiliation: Professor, Federal University of Espírito Santo – Ufes, Brazil. E-mail: oldrich.romero@ufes.br.
2Hugo Candiá Saad. B. Sc. in Petroleum Engineer Ufes. Affiliation: Supervisor, National Agency of Petroleum Natural Gas and Biofuels – ANP, Brazil.
Email: hsaad@anp.gov.br.
3Isabela Braga Pereira. Affiliation: Undergraduate Student, Federal University of Espírito Santo – Ufes, Brazil. Email: isa-bela-braga@hotmail.com.
4Mao Ilich Romero. D. Sc. PUC-Rio. Affiliation: Oil and Gas Consultant, Wyoming, United States of America. Email: ilichromero@gmail.com.
How to cite: Romero, O. J., Saad, H. C., Pereira, I. B., & Romero M. I. (2016). Influence of heat transfer on two-phase flow behavior in on-shore oil pipelines.Ingeniería e Investigación, 36(1), 14-22.
DOI: https://doi.org/10.15446/ing.investig.v36n1.51570.
ABSTRACT
Computational tools for simulation of multiphase flow in oil pipelines are of great importance for the determination of the technical feasibility of the production in oilfields. The present article presents the mathematical and numerical modeling of the oil biphasic flow in a partially submerged onshore pipeline. The biphasic behavior of the heavy oil of 13,2 ºAPI is translated by the Dukler correlation. The oil’s viscosity is regarded as dependent on the temperature and on the API density of the oil by means of the Hossain correlation. The pipeline, of 3,600 m and 4 inches (10.16 cm) in diameter, transports the oil from a collecting station to a storage center and consists of three sections. The first and third sections are above ground and are in contact with the external environment. The intermediate section is sitting on the river bed and is the critical part of the pipeline, once high heat losses are observed. The influence on the type of pipe insulation in the pressure and temperature gradients was analyzed with the aid of commercial 1D software Pipesim®. The results, of this 1D and non-isothermal problem with prescribed outlet pressure, show that the use of isolation when appropriately designed in terms of material quality and thickness is of utmost importance to maintain the heat transfer at low levels, in order to ensure the movement of fluids in long sections without compromising the system operation.
Keywords: Heat exchange, oil pipeline, two-phase flow, pressure drop, Pipesim.
RESUMEN
Las herramientas computacionales para la simulación numérica del flujo bifásico en tuberías son importantes para determinar la viabilidad técnica de producción de campos de petróleo. En este artículo se presenta el modelamiento matemático y numérico del flujo bifásico en una tubería terrestre parcialmente inmersa en un río. La correlación de Dukler es utilizada para modelar la presencia de más de una fases de fluidos. La dependencia de la viscosidad con la temperatura y el grado API del petróleo siendo transportado es introducida por la correlación de Hossain. La tubería transporta petróleo desde una estación de colecta (que recibe la producción de varios pozos) hasta un centro de almacenamiento. Esta tubería, de 3600 m y 4 pulgadas de diámetro, es formada por tres secciones. La primera y tercera se apoyan directamente sobre el suelo, intercambiando calor con el aire externo. La segunda sección pasa por el lecho de un río, estando expuesta a un intercambio de calor más intenso. La tubería es aislada en toda su extensión y la influencia del tipo de material del aislamiento que la recubre, así como la utilización de una bomba para impulsar el fluido, es estudiado mediante el software unidimensional Pipesim® para condición de presión prescrita en la salida. Los resultados obtenidos para el problema no isotérmico muestran que el tipo de aislamiento es muy importante para garantizar que el intercambio de calor entre el petróleo caliente y el medio externo más frío permanezca en niveles adecuados, de forma a que el transporte de fluidos en las secciones extensas de la tubería no comprometan la operación del sistema.
Palabras clave: Intercambio de calor, tubería de petróleo, flujo bifásico, disminución de presión, Pipesim.
Received: June 28th 2015
Accepted: February 23rd 2016
Introduction
The integrated and optimized management of operation and production processes is strategic to the advancement of the oil sector due to the vast and growing technological tools and the great challenges, such as fluid transportation, under many adverse conditions. The fluid transportation from the reservoir to the surface facilities is commonly divided into three stages, as shown in the 2D schematic representation of Figure 1: recovery, lifting and gathering. The diagram corresponds to an onshore production system. Each step is highly complex due to the dynamics of the process and the microscopic and macroscopic scales present mainly in the porous medium. The recovery treats the flow within the reservoir rock from the distant frontiers to the bottom (Romero & Fejoli, 2015; Romero & Pereira, 2014). The lifting refers to the flow inside the tubing from the bottom to the wellhead (Romero & Almeida, 2014; Romero & Hupp, 2014). The tubing, in turn, is contained in the previously drilled and cemented well. The term completed well is used to name a well equipped to produce the fluid coming from the reservoir in a safe and controlled way. The gathering stage refers to the fluid flowing from the wellhead to the facilities where they are processed. The last mentioned step consists of separating the water, gas, oil, and sediments. The fluid of interest is the oil. Water is treated before being discarded. The gas is typically burned as it is present in amounts that prove its use uneconomical. Sediments are also discarded after compliance with environmental legislation.

Figure 1. Stages of the oil flow from the reservoir rock to the surface facilities.
During oil production, the flow is usually a mixture of water, oil, gas and sediments, which provides a multiphase flow. When it ascends towards the surface, several flow patterns that depend on the dynamics of the production process are observed. In a simplified way, the flow may be treated as biphasic, in which one phase is gaseous and the other liquid. This type of flow is often found in the production string into the well and in the production pipelines. This can occur in vertical, inclined or horizontal sections. Correlations, such as those proposed by Hagedorn & Brown (1965), Duns & Ross (1963), Beggs & Brill (1963) and Oliemans (1976), have been developed to facilitate the flow analysis of this nature.
In the gathering stage, the pipeline engineering is presented as a specialty of utmost importance, in which one of the main operating/research topics is called flow assurance. Its main targets are to identify, qualify and mitigate operational problems, especially those resulting from the flow of heavy oil, since it can cause difficulties in the flow through the pipe. As an example, problems of corrosion and premature wear, in addition to the deposition of hydrates, paraffins and asphaltenes, resulting in large pressure drop and even obstruction of the pipes can be cited.
Since new discoveries of conventional oil are scarce and insufficient to meet the increase in energy demand, heavy and extra-heavy oils are important to supply this volumes of oil. However, as commented by Henaut et al. (2003), “a major flow assurance challenge in the near future is the production and transport of heavy oils. Despite very large reserves, their exploitation is limited by their high viscosity”. Looking for best ways to overcome this limitation, several reviews, experimental and numerical works are available in scientific literature, as for example: Pouraria et al. (2016), Hart et al. (2014), Santos et al. (2014), Aiyejina et al. (2011), Palau et al. (2011), Phillips et al. (2011), Goldstein et al. (2010), Li et al. (2010), Ashrafizadeh and Kamran (2010), Guozhong and Gang (2010), Saniere et al. (2004), among others, reflecting the interest of the scientific community and industry on this topic.
In this context, some practical examples of the challenges addressed by world oil companies operating in Brazil are briefly commented here. (i) In Ostra and Argonauta offshore fields operated by Shell and partners, hot oil is injected at the wellhead and then mixed with the low oAPI oil being produced. The resulting less viscous oil mixture, offers less resistance to flow along the flowline and riser to the platform. This technique also allows the reduction of paraffin deposition in the inner wall (ANP, 2016). (ii) Oil produced from Sabiá da Mata oil field, operated by Sonangol Starfish Oil & Gas Onshore, has a very low oAPI and BSW. At standard conditions, the oil flow is practically impossible. The production is made possible mixing the low API oil with a high API oil from Petrobras. (iii) In Fazenda Alegre onshore oil field at Espírito Santo basin, Brazil (Portal do Espírito Santo, 2016). In order to transport the low API oil to TNC – Terminal Norte Capixaba (Iorio e Cerqueira, 2002), the oil is previously heated at a certain temperature in order to reduce its viscosity and promote gas liberation, which helps oil flow. Pig operations are periodically executed to reduce paraffin deposition. (vi) Fluids (oil, water and gas) produced from offshore fields in Rio Grande do Norte and Ceará, Northeast region in Brazil, are pumped together through a unique pipeline to the onshore Unit Treatment and Fluid Processing plant. This is realized to allow the flow of the viscous oil.
Pipelines are the most convenient means of transporting crude oil from the producing field to the refinery (Hart, 2014); for such reason, this article aims to expose the influence of the pressure drop and heat transfer during the transportation of a biphasic fluid inside the pipeline. This is a real problem encountered in Espírito Santo basin.
Methods
Problem specification
The problem addressed here is the flow of oil-water mixture in an onshore pipeline susceptible to heat loss. The goal is to determine, by numerical simulation, the influence of heat loss in the fluid’s behavior.
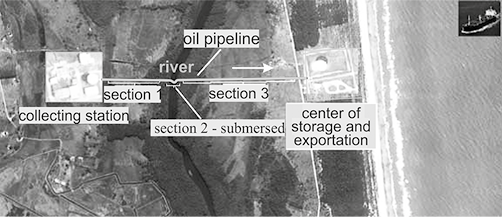
As shown in Figure 2a, the onshore system through which the mixture flows is formed by:
- a collecting station that receives the production from 15 onshore wells of low flow with pressure of 5 kg/cm2 and temperature of 66.7 °C. This is the point where the flow starts and the input boundary conditions must be imposed;
- a pipeline of 3,600 m and 4 inches (10.16 cm) in diameter and through which 21 m3/d of oil are disposed; and
- a storage and exporting center located on land that receives fluids. This is the point where the flow ends and output boundary conditions must be imposed.
(a)
(b)
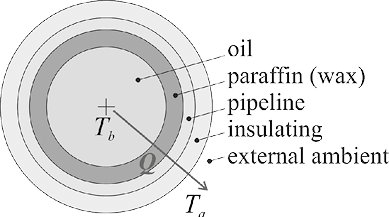
Figure 2. a) Spatial view of the components that defines the problem domain (source: Google Earth, 2015). b) cross section of the pipe showing the heat exchange between the hot fluid and the cooler environment.
The pipeline is composed of three segments called “section 1” with 802 m length, “section 2” with 203 m length, and “section 3” with 2,595 m length. All parts have a diameter of 4 in (10.16 cm), thickness of 0.251 in (6.37 mm) and roughness of 0.001 in (0.0254 mm). In sections 1 and 3 the pipe is suspended on land (above ground) with an ambient temperature of 26 °C. In section 2 the pipe passes through the river bed at a depth of 6 m and a temperature of 16 °C. It is in this section that an intense heat loss of the transported fluid is observed and, therefore, the need for studies on the use of appropriate insolation arises. The insulation used for this case study was the base asphalt, typically used in the oil industry.
The lengths of the sections are presented as equivalent to straight sections, i.e., all curves and other elements of the pipe were converted into straight section lengths, with equivalent pressure loss. The fluid properties using the black oil model are: gas/oil ratio 24,9 m3/m3, water and sediments volume of 30 %, relative gas density of 0.66, relative water density of 1.02, oil density of 13.2 °API, H2S of 0.06 %, and viscosity of dead oil as 69.4 cP at 93.3 °C and 20,269 cP at 15.5 °C. The conveyed fluid is formed by liquid and gaseous phases, so the Dukler correlation (Taitel & Dukler, 1976) is used to determine the pressure drop which considers slippage between the phases. As for the viscosity of the oil, which is a function of temperature and the API density, the Hossain correlation (Hossain et al., 2005) is selected.
For the exchange of heat between the hot fluid and the cooler environment, the following information items are required: thermal conductivity of the pipe kpipe = 35 W/(m K), thermal conductivity of the insulation klayer = 0.7 W/(m K), thermal conductivity of the oil koil = 0.08 W/(m K), convective heat transfer coefficient from the external environment hext= 4 W/(m2 K), for approximate air velocity of 0.5 m/s (Pipesim, 2011).
Mathematical model
Horizontal correlation for multiphase flow: The Dukler correlation (Taitel and Dukler, 1976) enables the determination of the pressure drop in a horizontal pipe caused by multiphase flow considering the slippage between the phases. For a correct description of the flow inside the pipe it is necessary to determine the pressure gradient dp/dl, where p is the pressure and l is the length along the pipeline.
 (1)
(1)
The first term on the right side of Equation (1), subscript “g”, is the pressure gradient corresponding to the gravity, and equals ρkΔz/gc. In a horizontal pipeline this component is very small and may therefore be neglected. The second term with subscripts “f” is relative to the friction and only exists when there is a flow. The last portion, sub index “acc”, refers to the pressure loss due to the acceleration and the friction term, and only exists in dynamic conditions.
The friction loss component is calculated by  , where gc is the gravitational constant that converts gravity acceleration in weight and D is the inner diameter of the pipe. As the problem threats the flow in more than one phase, the computation of the equation though apparently trivial is not simple. The variables depend on others to mathematically translate the complex interaction of the phases in the process. Thus, the first variable to be calculated is the specific weight of the mixture ρk which depends on the specific weight of the liquid phase ρL and gas phase ρg, on the liquid fraction of the input γL, on the fraction of the input gas γg and on the liquid hold-up HL (hold-up determination is described in the next paragraph) which is equal to
, where gc is the gravitational constant that converts gravity acceleration in weight and D is the inner diameter of the pipe. As the problem threats the flow in more than one phase, the computation of the equation though apparently trivial is not simple. The variables depend on others to mathematically translate the complex interaction of the phases in the process. Thus, the first variable to be calculated is the specific weight of the mixture ρk which depends on the specific weight of the liquid phase ρL and gas phase ρg, on the liquid fraction of the input γL, on the fraction of the input gas γg and on the liquid hold-up HL (hold-up determination is described in the next paragraph) which is equal to  . Another necessary variable is the friction factor f obtained from
. Another necessary variable is the friction factor f obtained from  , which is a function of y and that, in turn, depends on the length ln of the pipe and the input liquid fraction γL γ = -Lnγ L.fn is obtained from
, which is a function of y and that, in turn, depends on the length ln of the pipe and the input liquid fraction γL γ = -Lnγ L.fn is obtained from 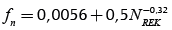 and the Reynolds number NREK is
and the Reynolds number NREK is  , where D is the inner diameter of the pipe and μod the viscosity of dead oil, which varies with the environment temperature and with the API density of the oil by means of the Hossain correlation (Hossain et al., 2005) detailed in next subsection.
, where D is the inner diameter of the pipe and μod the viscosity of dead oil, which varies with the environment temperature and with the API density of the oil by means of the Hossain correlation (Hossain et al., 2005) detailed in next subsection.
The value of liquid hold-up HL necessary to calculate the density of the mixture is obtained by the following iterative process:
1. From the data of the fluid, establish fluid density ρL.
2. Estimate the hold-up HL.
3. With the information from (1) and (2), calculate the approximate value of ρk.
4. Calculate μod with the Hossain’s correlation, Equation (3).
5. With the information from (3) and (4) calculate the Reynolds number NREK.
6. With the information from (1) and (5), using Figure 3, obtain HL.
7. Compare the values of the hold-up HL estimated in (2) and calculated in (6); if the result of this comparison is greater than a certain tolerance, use the calculated value as the new estimative and repeat the process from step (3) on. Otherwise, the convergence is satisfied, and the iterative process terminates with the hold-up required.

Figure 3. Graphical representation of the Dukler’s correlation (Taitel and Dukler, 1976) to determine the liquid hold-up.
The acceleration term that is part of Equation (1) is defined by  , with Usg and Usl being the average speeds of the gas and of the liquid, respectively, ρL and ρg being the specific weight of the liquid and of the gas, respectively, and gc the gravitational constant that converts acceleration of gravity in weight. Thus, the final expression for the calculation of the pressure gradient in horizontal pipes carrying multiphase fluids is represented by Equation (2), below.
, with Usg and Usl being the average speeds of the gas and of the liquid, respectively, ρL and ρg being the specific weight of the liquid and of the gas, respectively, and gc the gravitational constant that converts acceleration of gravity in weight. Thus, the final expression for the calculation of the pressure gradient in horizontal pipes carrying multiphase fluids is represented by Equation (2), below.
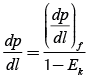 (2)
(2)
Correlation for the oil viscosity: The Hossain’s correlation (Hossain et al., 2005) allows to determine the viscosity of the dead oil, μod, for different values of fluid temperature T. It is valid for heavy oils with API density, dAPI, ranging from 10 < dAPI < 22.3. This dependence is evidenced by
 (3)
(3)
where a and b are parameters dependent on the oil API density dAPI and are defined by a= − 0,71523 dAPI + 22,13766 and b = 0,269024 dAPI − 8,268047. Figure 4 represents this relationship.

Figure 4. Oil viscosity dependence of temperature and API density, according to Hossain’s correlation.
The heavier the oil, i.e., high viscosity, the more its heating results in a higher decrease of viscosity. In other words, the viscosity of heavy oil is more affected by temperature change. Whereas heavy oil has a higher percentage of paraffinic components, the possibility of forming deposits is therefore greater.
Heat loss: Heat transfer is a manifestation of thermal mismatch between two bodies. Nature seeks to achieve and maintain a state of equilibrium. This condition is reached when the temperature of cooler body increases and the temperature of warmer body decreases. In the specific situation of multiphase fluid being transported by pipe, the “cooler body” is the big external environment, so its temperature will rise very little. In other practical terms, the external temperature is kept constant. Thus, the temperature of the “warmer body”, which is the fluid inside the pipe, will decrease in order to reach the equilibrium with the surrounding environment. Several thermal resistances are offered to mitigate this heat exchange. Equation (4) is the mathematical representation of the heat exchange Q (Figure 2b), with Tb as the temperature of hot fluid inside the pipe, Ta temperature of the cooler environment, outside the pipe, and A is the perpendicular area to the direction of heat flow.
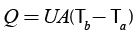 (4)
(4)
The overall heat exchange coefficient, represented by U, depends on thermal resistance offered by bodies between the fluid of interest and the external environment; in a simplified manner, it is calculated by means of Equation (5):
 (5)
(5)
where parameters hint (or, in this study, hoil), kpipe, klayer and hext are, respectively, the heat transfer coefficient of the multiphase fluid flowing in the pipe (“int”), the thermal conductivity of the metallic pipe (“pipe”), the thermal conductivity of the isolation layer, in this base situation asphalt (“layer”), and the heat transfer coefficient of the external environment (“ext”), which can be either air or water depending on the section.
According to Kaminsky (1999), for a laminar flow with a Reynolds number NREK < 2.300, hint can be obtained using  ,
,  ,
,  ,
,  , where μL is the oil viscosity; μw is the viscosity of water; CpL is the specific heat capacity of oil; kL the thermal conductivity of oil; D is the diameter of the pipe; Nu is the Nusselt number and its value can vary between 0 and 1; and Pr the Prandtl number.
, where μL is the oil viscosity; μw is the viscosity of water; CpL is the specific heat capacity of oil; kL the thermal conductivity of oil; D is the diameter of the pipe; Nu is the Nusselt number and its value can vary between 0 and 1; and Pr the Prandtl number.
The second and third terms on the right side of Equation (5) refer to the heat exchange through the wall of the pipe and thermal isolation; they are obtained from the equations  and
and  with wtlayer being the thickness of the isolation layer adjacent to the pipe.
with wtlayer being the thickness of the isolation layer adjacent to the pipe.
The last term on the right side of Equation (5), which is the convective heat transfer coefficient between the isolation layer and the external environment, hext, is obtained from the equations
 ,
, ,
, and
and  , where L is the length of the pipe, and Gr and Ra are the Grashof and the Rayleigh numbers, respectively.
, where L is the length of the pipe, and Gr and Ra are the Grashof and the Rayleigh numbers, respectively.
For sections 1 and 3 of the pipe, which are above ground, the hext coefficient has the typical value of 4 Wm-2K-1 for natural convection with the approximate speed of the air being 0.5 m/s.
Boundary conditions: To solve the equations system it is necessary to determine its solution domain; this means establishing the boundary conditions to have a mathematical system can be solved.
As a one-dimensional problem (Figure 2a), the boundary conditions at the input and output of the pipe should be imposed, as mentioned previously. In this paper two situations were analyzed. They are identified as cases 1 and 2.
- Case 1 - Low input pressure: fluid pressure at the input is prescribed in 5 kg/cm2. This means that the fluid pressure in the output should be calculated; and
- Case 2 - Pressure provided by a centrifugal pump: fluid pressure in the output is prescribed at 3 kg/cm2, meaning that the fluid pressure at the input should be calculated.
In both situations the oil enters at a fixed flow rate of 21 m3/d and a temperature of 67 °C. The outside environment temperature is 26 °C in air and 16 °C in water.
Numerical model
All the equations presented are solved using the Pipesim® software, whose use is widely spread in artificial lift engineering as well as in pipeline engineering. The procedure to obtaining the solution implemented in this software is based on the technique called Nodal Analysis®. This procedure consists in segmenting the flow line in a number of sections, denoted by the index j. Each section is subdivided into even small intervals denoted by the index i. The pressure gradient correlation is selected in function of the fluid and flow characteristics. This correlation is solved at each small interval.
Such technique is commonly applied for multiphase flow analysis, since the PVT (pressure / volume / temperature) properties of the fluid significantly alter the extent in which the fluid is transported; furthermore, the geometry where these fluids flow may change in diameter, in the roughness of the inner wall, and inclination of the pipe. The purpose of the division into sections j is to be able to contemplate pipes with different inclinations.
The numerical integration of Equation (2) along the length L of the pipeline results in Equation (6), which allows to calculate the differential pressure ∆p of the pressure gradient dp/dl for n different segments of pipe and m pipe sections:
 (6)
(6)
In our situation, m = 3. Figure 5 illustrates the application of the technique to the case of a submarine system for petroleum production.

Figure 5. Nodal Analysis® technique application in a submarine production system.
Results and discussion
Case 1: low input pressure
The problem analyzed in this article is detailed in Figure 2a. For case 1, the representation in Pipesim® symbology is very similar to that shown in Figure 10 for case 2 (without the presence of the pump); for this reason, it is not repeated here.
Initially, the pressure check in the collecting station (pipeline input), serves to verify if the fluid is able to move to its final destination in the storage and export center considering low heat exchange along the section. In other words, the overall heat exchange coefficient U, is approximated by U = 1,135 W/(m2K). The main objective of this first stage is to determine if artificial mechanisms are necessary in order to increase the pressure in the pipe input, or not.
The calculated pressure gradient is shown in Figure 6. It can be seen that pressure drop along the pipe is non-linear due to the presence of more than one phase, and for this conditions the fluid does not have sufficient energy to flow to the end of the tubing of 3,600 m length. It only runs through the first 2,950 m, 82 % of the full length. Thus, it can be established that in these conditions the production is not viable. It is noteworthy that to achieve the end of the pipe the fluid should have a minimum pressure of 3 kg/cm2 to overcome internal resistance in the storage tank.

Figure 6. Pressure variation over the pipeline for case 1, with low heat exchange, U1,2,3 = 1,135 W/(m2 K), in sections 1, 2 and 3.
In Figure 7 the temperature gradient for case 1 condition is shown. The oil enters the pipeline with a temperature of 67 °C and decreases along the pipeline until it reaches the temperature of approximately 31 °C at 2,950 m, which is the maximum distance that the fluid is moved, 82 % of the full length. As section 1 is 802 m long, section 2 is 203 m, and section 3 is 2,595 m, the oil tends to seek equilibrium with the external environment, which is at a temperature of 26 °C, and therefore reaches only part of section 3.
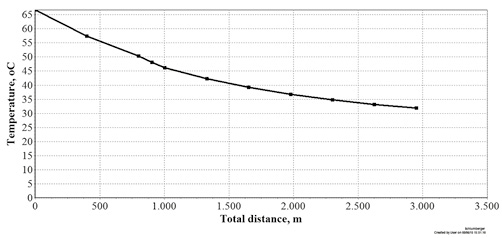
Figure 7. Variation of temperature along the pipe for case 1, with low heat exchange, U1,2,3 = 1,135 W/(m2 K) in sections 1, 2 and 3.
Another analysis can be obtained by considering a more intense heat exchange in all pipe sections. This means that in sections 1 and 3, which are exposed to air, the value of the coefficient U is equal to 113.6 W/(m² K), 100 times bigger than previous one; and in the second section, which is submersed in water, U is 1,135.7 W/(m² K), 1,000 times bigger than previous one.
Figures 8 and 9 illustrate graphs of the pressure gradient and temperature gradient, respectively, for this new U values. As expected, once the conditions are more unfavorable to avoid heat exchange, a greater pressure drop occurs along the route, causing a smaller displacement of fluid compared to the situation mentioned previously (low heat exchange). In other words, it requires additional energy to move the fluid. This can be seen in Figure 9, where the abrupt and continuous decrease of the fluid temperature until the equilibrium with the external medium that is 26 °C, allows the arrival of fluid just in the end of section 1.

Figure 8. Pressure variation along the pipeline for case 1, whereas high heat exchange. Sections 1 and 3 U1,3 = 113.57 W/(m2 K) and section 2 U2 = 1,135.7 W/(m2 K).
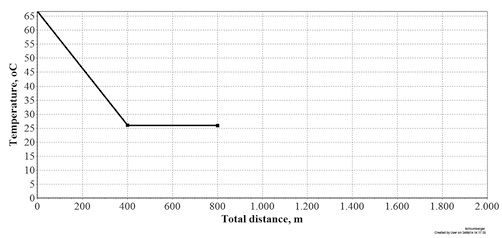
Figure 9. Temperature variation along the pipeline for case 1, whereas high heat exchange. Sections 1 and 3: U1,3 = 113.57 W/(m2 K) and section 2: U2 = 1,135.7 W/(m2 K).
The main reason is that with the decrease of the oil temperature, the oil viscosity increases sharply and paraffin eventually begins to precipitate in the inner wall of the pipeline. The appearance of paraffin deposits is manifested by the breaking of phase equilibrium, caused by the oil cooling and/or release of the lighter fractions dissolved originally in oil. Paraffin, when exposed to a certain temperature, called WAT (wax appearance temperature), precipitates in crystal forms and is characterized by a solid phase; it deposits on the internal walls of the pipelines, obstructing the flow and promoting the increase of pressure drop in production lines. Among other problems, decreasing of the flow rate of the fluid and the obstruction of the production pipeline section may occur.
Case 2: pressure provided by a centrifugal pump
Based on the previous results it was decided to use a centrifugal pump with 1,491.4 W power and efficiency of 50 %. The pump will be installed in the inlet plane, close to the collecting station. The new configuration in Pipesim® symbology is shown in Figure 10.
Figure 10. Representation in Pipesim® symbology of the new configuration with the pump in the pipeline inlet.
Provided that there is a need to increase pressure in the system, the question to be answered is: what level of pressure should be used? The prescribed pressure of 3 kg/cm2 in the pipe output, which is the arrival of fluid in the storage and export center, determines that the minimum pressure in the input pipe should be 10.5 kg/cm2. This result assumes a low heat loss in the system (U = 1,135 W/(m2 K); the minimum pressure gradient is shown in Figure 11.
The temperature profile, Figure 12, shows that an increase in pressure has a smaller temperature decrease compared to situation 1, Figure 7, reaching the final destination of approximately 29.5 °C.

Figure 11. Pressure variation along the pipeline for case 2, with low heat exchange, U1,2,3 = 1,135 W/(m2 K) in sections 1, 2 and 3.

Figure 12. Temperature variation along the pipeline for case 2, with low heat exchange, U1,2,3 = 1,135W/(m2 K) in sections 1, 2 and 3.
Again, with a pressure of 3 kg/cm2 in the output of the pipeline, and similar to case 1, a high heat transfer conditions, i.e., segments 1 and 3 with U = 113.57 W/(m2 K) and segment 2 with U = 1,135.7 W/(m2 K), and pressure and temperature gradients are presented in Figures 13 and 14, respectively.

Figure 13. Pressure variation along the pipeline for case 2, high heat exchange. Sections 1 and 3 U1,3 = 113.57 W/(m2 K) and section 2 U2 = 1,135.7 W/(m2 K).
Because heat loss is more severe, the temperature of the oil being transported considerably decreases, negatively impacting in the viscosity values since inverse dependence with temperature is governed by Equation (3), which accordingly increases the pressure gradient. The input pressure of the system goes from 10.5 kg/cm2 (Figure 11) to about 24.6 kg/cm2 (Figure 13). When snalyzing the graphics, there is a more significant decrease in pressure in section 2 due to the fact that the pipeline crosses the river bed at temperatures below air temperature.
Unlike small temperature variations obtained with low heat exchange - Figure 12, in this situation -, with high heat exchange, temperature has an abrupt decrease, from 67 °C at the input to pipe to 26 °C in the first 400 m, as seen in Figure 14. As the second section is submerged in the river, the oil temperature further decreases to equilibrate to 16 °C external water over 203 m. In section 3, oil exchanges heat with air at a temperature of 26 °C, comes into equilibrium and maintains this temperature until the pipe output at 3,600 m.
When a pressure increases 20 % more than the minimum required in the discharge pipe to meet operational fluctuations, the new boundary condition at the output plane is set to 3.6 kg/cm2. The new pressure profile, with low heat transfer U1,2,3 = 1,135 W/(m2 K) in all sections, is very similar to that of Figure 11; additionally, the temperature profile along the pipe hasn’t changed significantly in relation to Figure 12, and therefore the results are not shown.
As in the previous analysis performed, the response of the system with this new pressure condition, to high heat exchange, section 1 and 3 U1, 3 = 113.57 W/(m2 K) and section 2 U2 = 1,135.7 W/(m2 K), was also sought. Again, the pressure and temperature behavior are similar to those described in Figures 13 and 14.
Final remarks and future work
It is clearly noticeable that the influence of temperature drop on the flow can provide great difficulties in flowing through the pipe, especially when dealing with heavy oils. The appearance of paraffins, hydrates and/or asphaltenes are examples of problems caused by this thermal unbalance, which requires further increase of the fluid pressure at the inlet and more effective isolation conditions.

Figure 14. Temperature variation along the pipeline for case 2, high heat exchange. Sections 1 and 3 U1,3 = 113.57 W/(m2 K) and section 2 U2 = 1,135.72 W/(m2 K).
For the problem analyzed here, there is a need for using a pump suitably selected to drive the fluids to the delivery location, serving inaccuracies in the simulation results as well as operational fluctuations that may occasionally occur. The use of isolation when appropriately designed, in terms of material quality and thickness, is of extreme importance to maintain the heat transfer at low levels, in order to ensure the movement of fluids over long sections without compromising system operation.
A refinement of this paper involves studying the initiation of growth of paraffin deposits (Aiyejina et al., 2011), which occurs when the oil temperature becomes equal to, or lower than, the WAT; after that cleaning operation of pipeline, such as pigs, are necessary (Figure 15).
.This, however, requires the use of other commercial software or development of specific in-house applications (Romero, 2005).
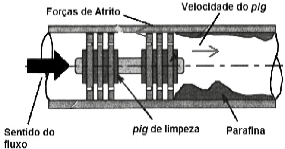

Figure 15. Schematic of pig operation (left) and photograph of cleaning process (right).
Acknowledgements
The authors thank Schlumberger for granting the academic license Pipesim® software. Professor Oldrich Joel Romero thanks the FAPES - Foundation for Research of Espírito Santo, for the financial support granted through the process 54.708.508/2011.
References
Aiyejina, A., Chakrabarti, D. P., Pilgrim, A., & Sastry, M. K. S. (2011). Wax formation in oil pipelines: A critical review. International Journal of Multiphase Flow, v. 37, 671–694. DOI: 10.1016/j.ijmultiphaseflow.2011.02.007.
ANP - National Agency of Petroleum, Natural Gas and Biofuels (Brazil). Retrieved from http://www.anp.gov.br. Visited in February 26, 2016.
Ashrafizadeh, S. N., & Kamran, M. (2010). Emulsification of heavy crude oil in water for pipeline transportation. Journal of Petroleum Science and Engineering, v. 71, 205–211. DOI:10.1016/j.petrol.2010.02.005.
Beggs, H. D., & Brill J. P. (1973). A study of two phase flow in inclined pipes. Journal of Petroleum Technology, v. 25, n. 5, 607-617. DOI: 10.2118/4007-PA.
Duns, H., & Ros, N. C. J. (1963). Vertical flow of gas and liquid mixtures in wells. 6th World Petroleum Congress, 19-26 June, Frankfurt am Main, Germany.
Goldstein, R. J., Ibele, W. E., Patankar, S. V., Simon, T. W., Kuehn, T. H., Strykowski, P. J., Tamma, K. K., Heberlein, J. V. R., Davidson, J. H., Bischof, J., Kulacki, F. A., Kortshagen, U., Garrick, S., Srinivasan, V., Ghosh, K., & Mittal, R. (2010). Heat transfer—A review of 2004 literature. International Journal of Heat and Mass Transfer, v. 53, 4343–4396.
Guozhong, Z., & Gang, L. (2010). Study on the wax deposition of waxy crude in pipelines and its application. Journal of Petroleum Science and Engineering, v. 70, 1–9.
DOI: 10.1016/j.petrol.2008.11.003.
Hagedorn, A. R., & Brown, K. E. (1965). Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits. Journal of Petroleum Technology, v. 17, n. 4, 475-484. DOI: 10.2118/940-PA.
Hart, A. (2014). A review of technologies for transporting heavy crude oil and bitumen via pipelines. J Petrol Explor Prod Technol, v. 4, 327–336. DOI: 10.1007/s13202-013-0086-6.
Henaut, I., Argillier, J-F., Pierre, C., & Moan, M. (2003). Thermal flow properties of heavy oils. Offshore Technology Conference, 5-8 May, Houston, Texas. DOI: 10.4043/15278-MS.
Hossain, M. S., Sarica, C., Zhang, H. Q., Rhyne, L., & Greenhill, K. L. (2005). Assessment and development of heavy-oil viscosity correlations. SPE International Thermal Operations and Heavy Oil Symposium, 1-3 November, Calgary, Alberta, Canada. DOI: 10.2118/97907-MS.
Iorio, S. M. B. M., & Cerqueira, J. R. (2002). Avaliação de diferenças composicionais do petróleo fazenda alegre e a produção de lubrificantes naftênicos. Boletim Técnico da Petrobras, v. 45, n. 3/4, 255-266.
Kaminsky, R. D. (1999). Estimation of two-phase flow heat transfer in pipes. J Energy Res Tech, v. 121, n. 2, 75-80. DOI: 10.1115/1.2795071.
Li, G ., Sheng, Y., Jin, H., Ma, W., Qi, J., Wen, Z., Zhang, B., Mu, Y., & Bi, G. (2010). Forecasting the oil temperatures along the proposed China–Russia Crude Oil Pipeline using quasi 3-D transient heat conduction model. Cold Regions Science and Technology, v. 64, 235–242. DOI: 10.1016/j.coldregions.2009.08.003.
Oliemans, R. V. A. (1976). Two-phase flow in gas-transmission pipeline. ASME paper 76-Pet, presented at Pet. Div. ASME meeting Mexico City.
Palou, M. M., Mosqueira, M. L., Rendón, B. Z., Juárez, E. M., Huicochea, C. B. López, J. C. C., & Aburto, J. (2011). Transportation of heavy and extra-heavy crude oil by pipeline: A review. Journal of Petroleum Science and Engineering, v. 75, 274–282. DOI:10.1016/j.petrol.2010.11.020.
Phillips, D. A., Forsdyke, I. N., McCracken, I. R., & Ravenscroft, P. D. (2011). Novel approaches to waxy crude restart: Part 1: Thermal shrinkage of waxy crude oil and the impact for pipeline restart. Journal of Petroleum Science and Engineering, v. 77, 237–253. DOI:10.1016/j.petrol.2010.11.009.
Pipesim (2011). Fundamentals Training and Exercise Guide - version 2011.1, Schlumberger.
Portal do Espírito Santo. Retrieved from http://www.es.gov.br/EspiritoSanto/paginas/petroleo_gas.aspx (in Portuguese). Visited in February 26, 2016.
Pouraria, H., Seo, J. K., & Paik, J. K. (2016). Numerical modelling of two-phase oil–water flow patterns in a subsea pipeline. Ocean Engineering, v. 115,135–148. DOI: 10.1016/j.oceaneng.2016.02.007.
Romero, M. I. (2005). Avaliação do mecanismo de difusão molecular para a modelagem da deposição de parafina em dutos de petróleo. (Unpublished Master’s Dissertation). Pontifícia Universidade Católica do Rio de Janeiro (PUC-Rio), Rio de Janeiro, RJ, Brazil.
Romero, O. J., & Almeida, P. (2014). Numerical simulation of the sucker-rod pumping system. Ingeniería e Investigación, v. 34, n. 3, 4-11. DOI: 10.15446/ing.investig.v34n3.40835.
Romero, O. J., & Fejoli, R. F. (2015). Fundamentos da recuperação avançada de petróleo: injeção de espumas1. ed. Saarbrücken, Sarre, Alemanha: Novas Edições Acadêmicas. v. 1. 196 p. ISBN 978-613-0-15342-7.
Romero, O. J., & Hupp, A. (2014). Subsea electrical submersible pump significance in petroleum offshore production (JERT-12-1245). Journal of Energy Resources Technology, v. 136, n. 1, 012902. DOI: 10.1115/1.4025258.
Romero, O. J., & Pereira, F. R. (2014). Modelagem computacional da injeção de dióxido de carbono como método de recuperação de petróleo. Estudos Tecnológicos (Online), v. 10, n. 1, 10-23. DOI: 10.4013/ete.2014.101.02.
Saniere, A., Hénaut, I., & Argillier, J. F. (2004). Pipeline transportation of heavy oils, a strategic, economic and technological challenge. Oil & Gas Science and Technology – Rev. IFP, v. 59, n. 5, 455-466.
Santos, R. G., Loh, W., Bannwart, A. C., & Trevisan, O. V. (2014). An overview of heavy oil properties and its recovery and transportation methods. Brazilian Journal of Chemical Engineering,v.31,n.3,571–590. DOI:10.1590/0104-6632.20140313s00001853.
Taitel, Y., & Dukler, A.E. (1976).A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow. AIChE Journal, v.22, n.1,47-55. DOI: 10.1002/aic.690220105.

How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Lorena A. dos Santos, Daniel da C. Ribeiro, Oldrich J. Romero. (2020). Heavy oil transportation through steam heating: An analytical and numerical approach. Journal of Petroleum Science and Engineering, 195, p.107932. https://doi.org/10.1016/j.petrol.2020.107932.
2. Syed Amjad Ahmed, Bibin John. (2018). Liquid – Liquid horizontal pipe flow – A review. Journal of Petroleum Science and Engineering, 168, p.426. https://doi.org/10.1016/j.petrol.2018.04.012.
Dimensions
PlumX
Article abstract page views
Downloads
License
Copyright (c) 2016 Oldrich Joel Romero, Hugo Candiá Saad, Isabela Braga Pereira, Mao Ilich Romero

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors or holders of the copyright for each article hereby confer exclusive, limited and free authorization on the Universidad Nacional de Colombia's journal Ingeniería e Investigación concerning the aforementioned article which, once it has been evaluated and approved, will be submitted for publication, in line with the following items:
1. The version which has been corrected according to the evaluators' suggestions will be remitted and it will be made clear whether the aforementioned article is an unedited document regarding which the rights to be authorized are held and total responsibility will be assumed by the authors for the content of the work being submitted to Ingeniería e Investigación, the Universidad Nacional de Colombia and third-parties;
2. The authorization conferred on the journal will come into force from the date on which it is included in the respective volume and issue of Ingeniería e Investigación in the Open Journal Systems and on the journal's main page (https://revistas.unal.edu.co/index.php/ingeinv), as well as in different databases and indices in which the publication is indexed;
3. The authors authorize the Universidad Nacional de Colombia's journal Ingeniería e Investigación to publish the document in whatever required format (printed, digital, electronic or whatsoever known or yet to be discovered form) and authorize Ingeniería e Investigación to include the work in any indices and/or search engines deemed necessary for promoting its diffusion;
4. The authors accept that such authorization is given free of charge and they, therefore, waive any right to receive remuneration from the publication, distribution, public communication and any use whatsoever referred to in the terms of this authorization.



























