Correo Electrónico
DNINFOA - SIA
Bibliotecas
Convocatorias
Identidad U.N.
Publicado
Sensibilidad del coeficiente de Manning en la estimación de los niveles de crecida para el mapeo de inundaciones en un río de la región interandina de Ecuador
The Sensitivity of Manning’s Coefficient in Estimating Water Levels in an Ecuadorian River in The Inter-Andean Region for Flood Mapping
Sensibilidade do coeficiente de Manning na estimativa de níveis de água para o mapeamento de inundações em um rio da região interandina do Equador
DOI:
https://doi.org/10.15446/rcdg.v32n1.94764Palabras clave:
análisis de sensibilidad, coeficiente de rugosidad, mapas de inundación, modelización hidráulica, modelo 1-D (es)sensitivity analysis, roughness coefficient, flood maps, hydraulic modeling, 1-D model (en)
análise de sensibilidade, coeficiente de rugosidade, mapas de inundação, modelagem hidráulica, modelo 1-D (pt)
Los datos de entrada, parámetros y la estructura de los modelos matemáticos introducen incertidumbre en los resultados; siendo aconsejable realizar un análisis de sensibilidad cuando se implementan o antes de su uso. Este estudio evaluó la sensibilidad del coeficiente de Manning debido al tipo de cobertura de las planicies y el cauce del río, en el cómputo de los niveles de agua y en la delimitación de las áreas inundadas. El estudio usó el modelo unidimensional [1-D] MIKE 11 para la implementación de un tramo de cinco kilómetros del río Santa Bárbara en el sur de Ecuador. Para el análisis de sensibilidad se realizaron seiscientas simulaciones de Monte Carlo para cada evento de crecida, y los resultados sirvieron para evaluar la robustez del modelo 1-D. Este análisis reveló sensibilidad a los cambios en el coeficiente de Manning; hubo una diferencia de hasta 1,02 m. entre niveles máximos y mínimos de agua. Sin embargo, los resultados de los mapas de inundación revelaron diferencias casi imperceptibles en la extensión del área inundada. Los hallazgos indican que el valor medio de Manning recomendado en la literatura es confiable para estimar mapas de peligro de inundación en ríos de montaña de la región interandina.
Input data, parameters, and the structure of mathematical models introduce uncertainty in the results; thus, sensitivity analysis is required when implementing a model or as a preliminary step. This study evaluated the sensitivity of Manning’s coefficient based on landcover types in the floodplains and the main channel, for calculating water levels and defining flood extent. The MIKE 11 one-dimensional [1-D] model was used in this study on a five-kilometer stretch of the Santa Barbara River in southern Ecuador. Six hundred Monte Carlo simulations were run for each flood event, and the results were used to assess the robustness of the 1-D model. This analysis revealed that Manning’s coefficient was sensitive to changes: there was a difference of up to 1.02 m between maximum and minimum water levels. The resulting flood maps, however, revealed almost imperceptible differences in flood extent. These findings demonstrate that the recommended Manning’s mean value is reliable for flood hazard mapping of Mountain Rivers in the inter-Andean region.
Os dados de entrada, parâmetros e a estrutura dos modelos matemáticos introduzem incerteza nos resultados; sendo aconselhável realizar uma análise de sensibilidade quando forem implementadas ou antes de sua utilização. Este estudo avaliou a sensibilidade do coeficiente de Manning devido ao tipo de cobertura das planícies e do canal do rio, no cálculo dos níveis de água e na delimitação das áreas inundadas. O estudo utilizou o modelo unidimensional [1-D] MIKE 11 para a implementação de um trecho de cinco quilômetros do rio Santa Bárbara no sul do Equador. Para a análise de sensibilidade, 600 simulações de Monte Carlo foram realizadas para cada evento de inundação, e os resultados foram usados para avaliar a robustez do modelo 1-D. Esta análise revelou sensibilidade a mudanças no coeficiente de Manning; houve uma diferença de até 1,02 m. entre os níveis máximos e mínimos de água. No entanto, os resultados dos mapas de inundação revelaram diferenças quase imperceptíveis na extensão da área inundada. Os resultados indicam que o valor médio de Manning recomendado na literatura é confiável para estimar mapas de risco de inundação em rios de montanha da região interandina.
Recibido: 2 de junio de 2021; Aceptado: 12 de julio de 2022
Resumen
Los datos de entrada, parámetros y la estructura de los modelos matemáticos introducen incertidumbre en los resultados; siendo aconsejable realizar un análisis de sensibilidad cuando se implementan o antes de su uso. Este estudio evaluó la sensibilidad del coeficiente de Manning debido al tipo de cobertura de las planicies y el cauce del río, en el cómputo de los niveles de agua y en la delimitación de las áreas inundadas. El estudio usó el modelo unidimensional [1-D] MIKE 11 para la implementación de un tramo de cinco kilómetros del río Santa Bárbara en el sur de Ecuador. Para el análisis de sensibilidad se realizaron seiscientas simulaciones de Monte Carlo para cada evento de crecida, y los resultados sirvieron para evaluar la robustez del modelo 1-D. Este análisis reveló sensibilidad a los cambios en el coeficiente de Manning; hubo una diferencia de hasta 1,02 m. entre niveles máximos y mínimos de agua. Sin embargo, los resultados de los mapas de inundación revelaron diferencias casi imperceptibles en la extensión del área inundada. Los hallazgos indican que el valor medio de Manning recomendado en la literatura es confiable para estimar mapas de peligro de inundación en ríos de montaña de la región interandina.
Palabras clave
análisis de sensibilidad, coeficiente de rugosidad, mapas de inundación, modelización hidráulica, modelo 1-D.Abstract
Input data, parameters, and the structure of mathematical models introduce uncertainty in the results; thus, sensitivity analysis is required when implementing a model or as a preliminary step. This study evaluated the sensitivity of Manning’s coefficient based on landcover types in the floodplains and the main channel, for calculating water levels and defining flood extent. The MIKE 11 one-dimensional [1-D] model was used in this study on a five-kilometer stretch of the Santa Barbara River in southern Ecuador. Six hundred Monte Carlo simulations were run for each flood event, and the results were used to assess the robustness of the 1-D model. This analysis revealed that Manning’s coefficient was sensitive to changes: there was a difference of up to 1.02 m between maximum and minimum water levels. The resulting flood maps, however, revealed almost imperceptible differences in flood extent. These findings demonstrate that the recommended Manning’s mean value is reliable for flood hazard mapping of Mountain Rivers in the inter-Andean region.
Keywords
sensitivity analysis, roughness coefficient, flood maps, hydraulic modeling, 1-D model.Resumo
Os dados de entrada, parâmetros e a estrutura dos modelos matemáticos introduzem incerteza nos resultados; sendo aconselhável realizar uma análise de sensibilidade quando forem implementadas ou antes de sua utilização. Este estudo avaliou a sensibilidade do coeficiente de Manning devido ao tipo de cobertura das planícies e do canal do rio, no cálculo dos níveis de água e na delimitação das áreas inundadas. O estudo utilizou o modelo unidimensional [1-D] MIKE 11 para a implementação de um trecho de cinco quilômetros do rio Santa Bárbara no sul do Equador. Para a análise de sensibilidade, 600 simulações de Monte Carlo foram realizadas para cada evento de inundação, e os resultados foram usados para avaliar a robustez do modelo 1-D. Esta análise revelou sensibilidade a mudanças no coeficiente de Manning; houve uma diferença de até 1,02 m. entre os níveis máximos e mínimos de água. No entanto, os resultados dos mapas de inundação revelaram diferenças quase imperceptíveis na extensão da área inundada. Os resultados indicam que o valor médio de Manning recomendado na literatura é confiável para estimar mapas de risco de inundação em rios de montanha da região interandina.
Palavras-chave
análise de sensibilidade, coeficiente de rugosidade, mapas de inundação, modelagem hidráulica, modelo 1-D.Introducción
El modelado del flujo en ríos tiene numerosos desafíos que incluyen: efectos del caudal sólido, cambios en la morfología del cauce, flujo a través de puentes y estructuras, acoplamiento de modelos hidrológicos e hidráulicos, reducción de la demanda computacional (Bladé, Cea y Corestein 2014), especificación de superficies de parámetros del modelo (Hardy, Bates y Anderson 1999), y registros históricos limitados (Gichamo et ál. 2012).
Existen muchas fuentes de incertidumbre en la modelación hidrodinámica, las cuales han sido ampliamente analizadas y discutidas en la literatura (Dimitriadis et ál. 2016), tales como los parámetros, la estructura del modelo y el efecto de los datos de entrada (Di Baldassarre 2012; Willems 2012; Papaioannou et ál. 2016). Las variables hidráulicas clave son: el caudal de entrada, la pendiente del cauce y de la planicie de inundación, y la fricción (es decir, el coeficiente de Manning) (Dimitriadis et ál. 2016). Las interacciones no lineales entre estos parámetros pueden generar variaciones adicionales en el rendimiento del modelo, las cuales son difíciles de cuantificar y pueden variar según los métodos utilizados para el análisis de sensibilidad (Pappenberger et ál. 2008).
El coeficiente de Manning introduce incertidumbre en la estimación de caudales (Fread 1989; Wohl 1998) y es difícil de determinar, ya que para estimar su valor se suele utilizar información levantada en campo (Dimitriadis et ál. 2016). Además, diferentes modelos presentan distintos niveles de sensibilidad a este parámetro (Dimitriadis et ál. 2016) y estudios anteriores indican que contribuye a la mayor parte de la incertidumbre total del modelo (Tayefi et ál. 2007). Otros estudios también indican la incertidumbre en los resultados de un modelo hidráulico asociado al coeficiente de rugosidad de Manning (Burnham y Davis 1990; Wohll 1998).
Dimitriadis et ál. (2016) declararon que la incertidumbre disminuye mientras mayor sea la pendiente, la rugosidad y el caudal. Por otro lado, Wohl (1998) encontró que los cauces que tienen valores de rugosidad bajos y pendientes que varían entre 0,001 y 0,006 muestran una mayor variación en Manning que aquellos en los cuales las pendientes varían de 0,026 a 0,111. Dado que el tramo evaluado del río Santa Bárbara tiene una pendiente promedio de 0,0025, podría existir una mayor variación en este parámetro. Además, los cambios en el coeficiente de Manning influyen en la celeridad de las ondas; aquellas áreas con más vegetación reducen la celeridad (Anderson, Rutherfurd y Western 2006) y disminuyen la extensión de la inundación.
La vegetación es la característica más importante que afecta al coeficiente de Manning en las planicies aluviales (rugosidad) y genera una mayor resistencia al flujo durante una crecida, por lo que su influencia en las inundaciones también ha sido considerada por autores como Fread (1989). En general, en los modelos 1-D la vegetación se estima ponderando los diferentes tipos de cobertura y asignando valores de rugosidad a cada cobertura dentro de rangos establecidos, por ejemplo, por Chow (1959) (Anderson, Rutherfurd y Western 2006; Wong et ál. 2014; Falter et ál. 2014). Además, de acuerdo con lo indicado por Ferguson (2010), el coeficiente de Manning es muy sensible a las variaciones de caudal. Por lo tanto, comprender la relación entre el nivel de agua y el coeficiente de Manning podría ayudar a mejorar la forma en que un modelo hidráulico responde a estos cambios (Lenhart et ál. 2002). La comprensión de esta relación también permitirá mejorar tanto la calibración para valores de caudales relativamente bajos, como en la predicción de eventos extremos, lo cual influye en el desempeño del modelo (Horritt y Bates 2002).
El análisis de sensibilidad —en adelante, AS— es una herramienta útil para comprender mejor el desempeño del modelo y reducir la incertidumbre (Pappenberger et ál. 2008). Este análisis evalúa en qué medida la incertidumbre en los parámetros de entrada del modelo influye en los resultados de salida (Iooss y Lemaître 2015). El AS, generalmente, consiste en mantener todos los parámetros constantes mientras se varía un solo parámetro (Lenhart et ál. 2002); para este propósito, la técnica de muestreo de Monte Carlo —en adelante, MC— es uno de los métodos más utilizados (Weichel, Pappenberger y Schulz 2007; Dimitriadis et ál. 2016). Existen otras metodologías, como el uso de muestras de hipercubos latinos replicados, que se basan en muestreos de MC (Hall et ál. 2005; Pappenberger et ál. 2008), o métodos de sensibilidad global, como los métodos de “screening” o descomposición de la varianza (Iooss y Lemaître 2015).
El rendimiento de los modelos hidráulicos también depende de las ecuaciones utilizadas, del esquema numérico, de la discretización geométrica espacial, de las condiciones de contorno y de la rugosidad del terreno (Bladé, Cea y Corestein 2014); donde el coeficiente de Manning es proporcional a la rugosidad (Wohl 1998). De acuerdo con Pappenberger et ál. (2008), las condiciones de contorno y la rugosidad del cauce son los principales parámetros que influyen en el cómputo de los niveles máximos de agua en los ríos.
La modelización hidráulica suele implicar el uso de modelos 1-D o 2-D. Según Di Baldassarre (2012), “a medida que aumenta la dimensión de un modelo, el sesgo tiende a disminuir, mientras que la incertidumbre tiende a aumentar”. Un mayor número de dimensiones implica una carga computacional más significativa (Hunter et ál. 2007; Bladé, Cea y Corestein 2014), lo que limita la aplicación de modelos de mayores dimensiones. Algunos autores afirman que las diferencias en las incertidumbres atribuidas a los diferentes tipos de modelos son menos significativas que la incertidumbre causada por un parámetro de entrada; por lo tanto, los modelos simplificados a veces son igual de convenientes (Dimitriadis et ál. 2016; Papaioannou et ál. 2016). Existen cuatro tipos principales en función del número de dimensiones utilizadas en la modelización de inundaciones: 1-D, cuasi 2-D, 2-D y 3-D.
En los modelos Cuasi 2-D, las planicies de inundación se tratan como depósitos de almacenamiento o como secciones de inundación 1-D conectadas al cauce principal (en MIKE-11, por ejemplo). Estos modelos son apropiados cuando existen planicies de inundación amplias y cuando el flujo secundario desde el cauce a las planicies de inundación es importante (Timbe 2007). Los modelos 2-D representan el río como una malla de celdas poligonales para caracterizar la topografía y los modelos 3D son poco comunes ya que requieren mallas muy complejas (Bladé, Cea y Corestein 2014). Por otro lado, están los métodos que combinan modelos 1-D y 2-D, los cuales se consideran una buena alternativa para geometrías complejas (Tayefi et ál. 2007).
Algunos autores, como Jung et ál. (2013), han obtenido resultados aceptables al usar modelos 1-D, mientras que otros, como Tayefi et ál. (2007), argumentan que los modelos 1-D no son la mejor opción para lugares con topografía compleja. En el presente estudio, se utilizó un modelo hidráulico 1-D para simular el flujo en el río Santa Bárbara, un río con una larga historia de inundaciones en el sur de Ecuador. Como las planicies de inundación no son significativamente más anchas que el río, se prefirió un enfoque 1-D. En estos modelos, el flujo en la planicie de inundación se produce en la misma dirección del flujo del cauce (Horritt y Bates 2002; Falter et ál. 2014). Según Timbe (2007), este enfoque es adecuado cuando no existen diques o terraplenes que separen las planicies de inundación del cauce principal del río y cuando las planicies de inundación no son muy anchas.
En la implementación se usaron secciones transversales perpendiculares al flujo (Aronica, Bates y Horritt 2002), para representar la geometría del río. El modelo emplea las ecuaciones de Saint-Venant, que son “un sistema de ecuaciones diferenciales parciales que modelan flujo no estacionario gradualmente variado” (Moussa 1996); este procedimiento se usa generalmente para el tránsito de crecidas (Dimitriadis et ál. 2016).
El río Santa Bárbara forma parte de un área urbana típica de la región interandina. Existen asentamientos humanos, así como infraestructura en las planicies de inundación del tramo del río analizado, principalmente en la margen izquierda, lo que hace que el área sea aún más propensa al riesgo de inundación. Los estudios de modelización de inundaciones son escasos en la región de estudio y no existe un procedimiento metodológico para su aplicación (Pinos y Timbe 2020), a pesar del hecho de que los eventos de crecida en este tramo ocurren en promedio cada dos o cuatro años (SENAGUA 2014). El principal objetivo de este trabajo fue determinar la sensibilidad de un modelo 1-D en la estimación de los niveles de agua del río, atribuida a los coeficientes de rugosidad de las planicies de inundación y del cauce, utilizando el software MIKE-11 como herramienta de modelización. También se buscó cuantificar su efecto en la delimitación de las áreas inundadas.
Este estudio es relevante debido a que este tipo de investigación es relativamente nuevo en la región interandina y el país, principalmente por los recursos económicos limitados y escasos registros históricos (p. ej. caudales, áreas inundadas). Esta investigación también está en línea con estudios hidráulicos previos realizados por SENAGUA (2014), donde se utilizó el paquete HEC-RAS para evaluar la vulnerabilidad a inundaciones en un tramo de 10 km del río Santa Bárbara. Al igual que el modelo HEC-RAS, el software MIKE-11 resuelve las ecuaciones 1-D de Saint-Venant y ambos tienen una baja demanda computacional; esto permite que se pueda realizar simulaciones de MC. Este estudio utilizó caudales crecida con períodos de retorno de veinte y cincuenta años para estimar los niveles de inundación. También se determinó el efecto de los niveles de inundación en la delimitación de las áreas inundadas.
Metodología
Área de Estudio
La zona de estudio (Figura 1) comprende un tramo de aproximadamente cinco kilómetros del río Santa Bárbara, que fluye a través del centro de la ciudad de Gualaceo en el sur de Ecuador. Este río de montaña se encuentra en la región Centro-Este de la provincia de Azuay y pertenece a la cuenca del río Paute, que genera aproximadamente el 50 % de la demanda de energía eléctrica en Ecuador (Yadaicela 2012). Existen tres puentes a lo largo del tramo, ubicados en las abscisas de 822 m (P1: Chacapamba), 1.386 m (P2: Jaime Roldós) y 2.544 m (P3: Velazco Ibarra), respectivamente. El sitio tiene una altitud de 2.230 m.s.n.m. (Campozano et ál. 2016), y una temperatura media anual de 14 ºC (Mora y Willems 2011). El régimen de precipitación es bimodal, y la precipitación anual promedio es de 820 mm (Campozano et ál. 2016), lo cual es característico del régimen interandino (Ochoa et ál. 2015). Históricamente, las crecidas han provocado el desbordamiento del río y esto ha afectado fuertemente al área urbana de la ciudad de Gualaceo, con una recurrencia promedio de dos a cuatro años (SENAGUA 2014). Por ejemplo, inundaciones históricas ocurrieron en junio de 2007, abril y julio de 2011, julio de 2013 y julio de 2017.
Figura 1
: Sitio de estudio del tramo del río Santa Bárbara y ubicación de los puentes.
Disponibilidad de la información
Los siguientes datos estuvieron disponibles: (i) caudales de crecida para periodos de retorno de veinte y cincuenta años, estimados a partir de un análisis de frecuencia de datos históricos de caudales máximos instantáneos, (ii) un modelo de elevación digital con una resolución de tres metros del proyecto SIG TIERRAS, (iii) 186 secciones del río levantadas en campo, y (iv) coeficientes de Manning estimados para cada sección transversal (SENAGUA 2014). La Tabla 1 presenta las condiciones de contorno de los caudales para los dos intervalos de recurrencia simulados en MIKE 11.
Tabla 1: Condiciones de contorno (CC) de caudales en el tramo de estudio en m3/s
Intervalo de recurrencia (años)
Aguas arriba
Tributario izquierdo
Tributario derecho
20
667,36
16,49
44,67
50
805,94
19,92
53,94
El coeficiente de Manning para cada sección transversal corresponde a los valores ponderados obtenidos en función de los porcentajes aproximados de los seis tipos de cobertura dominantes (bosque, cultivos, matorrales, pastos, suelo desnudo y suelo impermeable) en las planicies izquierda y derecha. Las observaciones históricas de nivel no estuvieron disponibles para realizar una calibración tradicional, por lo que, las áreas afectadas por eventos recientes de inundación ayudaron con la calibración del coeficiente de Manning en el estudio realizado por SENAGUA (2014). La Tabla 2 presenta los rangos de variación en el coeficiente de Manning para los tipos de vegetación/coberturas dominantes de acuerdo con Chow (1959). Estos rangos (límites superior e inferior) se usaron para el AS, muestreando valores aleatorios de Manning para cada tipo de cobertura, y posteriormente se calculó el valor ponderado de Manning en cada planicie. Para el cauce principal también se realizó un muestreo aleatorio en el rango establecido. Los coeficientes de Manning calibrados en el estudio realizado por la SENAGUA (2014) se indican en la Tabla 2.
Tabla 2: Límites superiores e inferiores de los valores del coeficiente de Manning y los valores calibrados para los diferentes tipos de cobertura vegetal dominantes en el tramo del río Santa Bárbara
Tipo de cobertura
Límite inferior
Límite superior
Valor calibrado
Bosque
0,08
0,12
0,1
Cultivos
0,025
0,045
0,035
Matorral
0,07
0,16
0,1
Pasto
0,025
0,035
0,03
Impermeable (pavimentado)
0,012
0,014
0,013
Suelo desnudo
0,02
0,04
0,03
Cauce principal
0,03
0,05
0,035
En el caso de las planicies, para cada planicie levantada en campo, se estimaron los porcentajes aproximados de las coberturas presentes, y se calculó un valor ponderado de Manning el cual se usó en el modelo hidráulico. A continuación, se presentan algunas imágenes del río (Figuras 2, 3 y 4):
Figura 2
: Fotografías de las áreas circundantes al puente P1: puente (superior izquierda); vista aguas abajo desde P1, al fondo se divisa P2 (superior derecha); sección aguas abajo de P1 (inferior izquierda e inferior derecha)
Figura 3
: Fotografías de las áreas circundantes al puente P2: aguas arriba de P2 (izquierda), aguas debajo de P2(derecha)
Figura 4
: Fotografías de las áreas circundantes al puente P3: puente P3 (superior izquierda), aguas debajo de P3 (superior derecha, inferior izquierda), aguas arriba de P3 (inferior derecha)
Implementación del modelo
El modelo hidrodinámico 1-D de MIKE-11 emplea métodos numéricos para resolver las ecuaciones de flujo. Este paquete puede usar diferentes descripciones de flujo: onda dinámica, onda difusa y onda cinemática (DHI 2002). En la implementación del tramo del río Santa Bárbara se utilizó la descripción de onda dinámica, ya que conserva el comportamiento dinámico del sistema (Montero et ál. 2013) y considera las pérdidas por fricción utilizando la fórmula de Manning. El esquema numérico emplea el método de diferencias finitas de Abbot de seis puntos para resolver las ecuaciones de continuidad y momento (ecuaciones 1 y 2, respectivamente) (DHI 2002).
Ecuación 1. Ecuación de continuidad
Ecuación 2. Ecuación de momento
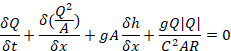
donde: Q es el caudal, A el área de flujo, q el flujo de entrada lateral, h el nivel por encima del datum, C el coeficiente de resistencia de Chezy, R el radio hidráulico, y α el coeficiente de distribución del momento.
En MIKE-11, primero se define el tipo de modelo (p. ej. hidrodinámico), luego se agregan los datos de entrada (como los datos geométricos de la red fluvial), las condiciones iniciales (nivel y/o caudal), los datos de las secciones transversales, las condiciones de contorno (p. ej. Caudal de entrada aguas arriba y nivel aguas abajo) y los parámetros hidrodinámicos, en ese orden. En esta investigación, el modelo MIKE 11 utilizó la misma información (es decir, secciones transversales y coeficientes de Manning) y las condiciones de contorno del estudio previo en HEC-RAS (SENAGUA 2014). Solamente se ajustaron algunos parámetros hidrodinámicos (p. ej. el paso de tiempo) para descartar inestabilidades numéricas. Los resultados de la simulación usando los valores de Manning previamente calibrados (ver tabla 2) se utilizaron como modelo de referencia para comparar los resultados del AS.
Análisis de sensibilidad
Antes de ejecutar las simulaciones para el AS se implementó un código en R con fines de automatización. El objetivo fue reemplazar valores muestreados al azar del coeficiente de Manning en el archivo de secciones transversales del paquete MIKE 11. Se utilizó una distribución uniforme en el rango mínimo-máximo (véase tabla 2) para la selección aleatoria de los coeficientes de Manning. Para cada sección transversal en este archivo se definen los valores del coeficiente de Manning para las planicies fluviales izquierda y derecha (previamente ponderados en función de los porcentajes de cobertura identificados en cada planicie), y un valor aleatorio para el cauce del río. El script generó seiscientos archivos de secciones por evento de inundación y cada archivo incluye las 186 secciones transversales del tramo evaluado.
Para todas las simulaciones se especificó una condición hidrodinámica inicial (hot.start) para definir un caudal base mínimo en el cauce, con el objetivo de evitar problemas de estabilidad numérica. Después de cada simulación, se extrajeron los resultados del nivel de agua para cada evento de inundación (seiscientas tablas por evento, es decir, seiscientos valores del nivel de agua en cada sección transversal). Con los resultados de nivel se realizaron tres pruebas de normalidad en los datos (Shapiro-Wilk, Jarque Bera y Jarque Bera ajustado) para determinar el mejor método para medir la dispersión de estos; la dispersión o distribución de los datos se ha utilizado anteriormente para el análisis de sensibilidad regionalizado (Pappenberger et ál. 2008). Posteriormente, la delimitación de las inundaciones y las áreas inundadas se calcularon utilizando la extensión “Flood from stream water surface elevation” de la herramienta Arc Hydro en ArcGIS. Los datos de entrada fueron los siguientes: la polilínea correspondiente al eje del cauce del río (niveles mínimos de cada sección transversal) junto con los datos correspondientes de nivel de agua de MIKE-11 en formato ráster, y un DEM de tres metros de resolución para el mapeo de la inundación. Esta herramienta funciona proyectando elevaciones de la superficie del agua sobre la topografía proporcionada por el DEM. Es similar a la herramienta MIKE GIS para delimitar la extensión de la inundación: utiliza un procedimiento de interpolación/extrapolación de los resultados de los niveles de agua en el cauce, así como un DEM para obtener los mapas de inundación (DHI 2001).
Por último, se realizó bootstrapping para evaluar la confiabilidad de las seiscientas simulaciones al calcular las medianas y las medias de los niveles de agua. El bootstrapping calcula los intervalos de confianza para una estadística de muestra (en este estudio se utilizó la mediana), lo que ayuda a validar los resultados (Carpenter y Bithell 2000; Pappenberger et ál. 2008). Esta técnica remuestrea los datos para obtener un mayor número de muestras. En este estudio, los datos del nivel del agua obtenidos del AS se muestrearon con reemplazo.
Resultados y Discusión
Los resultados de las seiscientas simulaciones de MC muestran que los niveles de inundación no se distribuyen normalmente, como lo confirman tres pruebas de normalidad: Shapiro-Wilk, Jarque Bera y Jarque Bera ajustada. La distribución de los datos para los dos eventos de inundación se examinó en tres puntos representativos a lo largo del tramo del río: a 1.100,12 m, 1.545,81 m y 2.999,67 m; en estos puntos se observan las variaciones más significativas. Dado que todos los valores p en los puntos evaluados son muy cercanos a cero (< 2,2 10-6) para las tres pruebas, las hipótesis nulas que respaldan la normalidad de los datos pueden ser rechazadas. Las Figuras 5 y 6 muestran los histogramas y los gráficos de caja (máximo/mínimo, percentiles del 90 % y mediana) para estas ubicaciones, confirmando los resultados de las pruebas de normalidad.
Figura 5
: Histograma de los resultados de niveles de inundación en metros sobre el nivel del mar obtenidos de las seiscientas simulaciones Monte Carlo, para el evento de crecida de veinte años, en las abscisas: 1.100,12 m (a, d), 1.545,81 m. (b, e), 2.999,67 m (c, f)
Figura 6
: Histograma de los resultados de niveles de inundación en metros sobre el nivel del mar obtenidos de las seiscientas simulaciones Monte Carlo, para el evento de crecida de cincuenta años, en las abscisas: 1,100.12 m (a, d), 1.545,81 m. (b, e), 2.999,67 m (c, f)
La media aritmética no se pudo utilizar como una medida de tendencia central adecuada dado que los datos no se distribuyen normalmente. Por lo tanto, se estimó la mediana que representa mejor los datos con una distribución sesgada. Con estos datos se calcularon los cuantiles del 90 % para definir intervalos de confianza, ya que proporcionan una buena medida de la dispersión (Di Baldassarre 2012) en los resultados. Otros trabajos también han empleado percentiles para el modelado de inundaciones; por ejemplo, Wong et ál. (2014) los emplearon para ilustrar el rango de variación de diferentes escenarios de erosión en el modelado de inundaciones. Las Figuras 7 y 8 comparan las áreas inundadas modeladas (para los eventos de inundación de veinte y cincuenta años) entre la mediana, los percentiles del 90 % y el modelo de referencia.
Los datos del nivel de agua obtenidos con las simulaciones de MC varían significativamente en respuesta a la variación del coeficiente de Manning. Para ilustrar los resultados de las seiscientas simulaciones MC del nivel de agua a lo largo del tramo del río para los eventos de crecida de veinte y cincuenta años se han incluido las Figuras 9 y 10. Como se puede observar en estas figuras, la diferencia entre los niveles de agua máximos y mínimos varían desde 1,02 m para el evento de veinte años hasta 0,941 m para el evento de cincuenta años. También hay diferencias de hasta 0,69 m y 0,74 m si se compara con los niveles del modelo de referencia, para los eventos de veinte y cincuenta años, respectivamente. Según lo esperado, los puentes producen un efecto de remanso aguas arriba de estas estructuras durante los eventos de inundación. También se puede observar que las medianas de los niveles de agua modelados se desvían del modelo de referencia, donde la diferencia máxima para el evento de veinte años es de 0,259 m, mientras que para cincuenta años es de 0,423 m. Ambas figuras ilustran que el modelo es sensible a las variaciones en Manning, ya que la diferencia en los niveles de agua es visible. En contraste, en los puentes y aguas arriba de los mismos, las diferencias en los niveles de agua son mucho más pequeñas ya que este tipo de estructuras hidráulicas controlan el flujo al reducir el área de flujo, de modo que los coeficientes de Manning tienen poca influencia en el cálculo de los niveles de agua.
Los resultados hidráulicos de MIKE-11 indican que el modelo es sensible a cambios del coeficiente de Manning con respecto a los niveles de agua, lo cual difiere de otros estudios en los que las variaciones en el coeficiente de Manning dentro de un rango específico dieron como resultado diferencias menores en los niveles de agua (Tayefi et ál. 2007). En términos de mapeo de inundaciones, los cambios en el coeficiente de Manning no son tan notables (Figuras 7 y 8), muy probablemente debido a las características topográficas típicas de la región interandina, conformada por planicies aluviales estrechas y laderas empinadas.
Figura 7
: Áreas inundadas para el evento de inundación de veinte años: cuantil 90 % inferior (rosa) y superior (rojo), medianas (cian) y referencia (azul)
Figura 8
: Áreas inundadas para el evento de inundación de cincuenta años: cuantil 90 % inferior (rosa) y superior (rojo), medianas (cian) y referencia (azul)
Figura 9
: Niveles de agua superficial en el tramo del río para el evento de inundación de veinte años: mediana, referencia, máximo, mínimo y cuantiles del 90 % para las seiscientas simulaciones de MC
Figura 10
: Niveles de agua superficial en el tramo del río para el evento de inundación de cincuenta años: mediana, referencia, máximo, mínimo y cuantiles del 90% para las seiscientas simulaciones de MC
Las áreas de inundación totales se presentan en la Tabla 3. Los resultados revelan pequeñas diferencias entre las áreas inundadas, y estas variaciones disminuyen al aumentar el intervalo de recurrencia. Estos resultados son esperados, ya que para estos eventos los bordes exteriores de la inundación llegan hasta la franja de transición de las tierras altas. Se podría esperar mayores diferencias en el área inundada para eventos con períodos de retorno menores (por ejemplo, 4, 5 años) cuando la inundación ocurre en la terraza de la planicie de aluvial, a lado del cauce principal.
Tabla 3: Áreas inundadas (en hectáreas), para los eventos de inundación de veinte (PR-20) y cincuenta (PR-50) años
Parámetro modelado
Evento de inundación PR - 20
Evento de inundación PR - 50
Modelo de referencia
109,62
127,13
Cuantil inferior del 90 %
100,53
124,99
Mediana
115,53
130,04
Cuantil superior del 90 %
122,62
134,57
Las medianas calculadas con bootstrapping (1.000, 2.000, 5.000, 10.000, 20.000, 30.000, 40.000 y 50.000 re-muestreos) son prácticamente las mismas que las estadísticas de la muestra de las simulaciones de MC; este hecho confirma la confiabilidad de las estadísticas calculadas (es decir, la mediana) con las seiscientas simulaciones de MC. Este hecho es especialmente cierto para la mediana, que representa los datos de manera más precisa cuando la distribución de los datos no es normal. Sin embargo, debido a que todos los análisis de sensibilidad presentan cierto grado de incertidumbre (Pappenberger et ál. 2008), se deben tomar precauciones al interpretar los resultados. En este trabajo no se consideraron más de seiscientas simulaciones debido a limitaciones de tiempo; sin embargo, según el análisis realizado, un número más significativo de simulaciones no habría proporcionado resultados notablemente mejores en el cómputo de la mediana y del intervalo de confidencia del 90 %.
En los mapas de extensión de inundación para los dos eventos evaluados (véase figuras 9 y 10), se observa el mismo patrón espacial y una expansión de la ola de inundación después del segundo puente, lo que probablemente se debe a una topografía más plana localmente. La densificación urbana y el consecuente aumento de la ocupación del suelo podrían incrementar aún más el peligro y riesgo de inundaciones debido al aumento de áreas impermeables que impiden la infiltración (p. ej. viviendas, caminos pavimentados, entre otros) y, por lo tanto, aumentan la escorrentía. Como se aprecia en los mapas de inundación, los cuantiles inferiores están muy cerca de los mapas de referencia, y los mapas de los cuartiles medio (mediana) y superior también son muy similares. Por lo tanto, en este caso específico, una calibración muy detallada y precisa del coeficiente de Manning en el modelo hidráulico no necesariamente proporcionaría mejores resultados en la delimitación del área inundada.
En general, la obtención de áreas inundadas y la comparación del rendimiento del modelo son aspectos muy importantes para evaluar los diferentes escenarios de inundación y para abordar la gestión del riesgo de inundación, especialmente porque los cambios en los patrones de inundación debido al cambio climático son inciertos (Alam, Willems y Alam 2014). A nivel mundial, la identificación y delimitación de las áreas en peligro de inundación es un componente clave que permite a los gobiernos locales (p. ej. municipios) mejorar la planificación del uso de suelo de las planicies aluviales. Como indica Pinos y Timbe (2020), en Ecuador no existe una normativa para este tipo de análisis y generalmente las restricciones del uso de suelo únicamente consideran un ancho constante desde el centro del cauce o desde la margen (p. ej. 50 m). Por lo tanto, es imperiosa la necesidad de incorporar la modelización de crecidas y el mapeo de inundaciones, que permita a los gobiernos locales mejorar la gestión del uso de suelo con criterios técnicos (p. ej. topografía local, magnitud de la crecida). Finalmente, los resultados obtenidos en este estudio podrían emplearse para la adopción de medidas estructurales (p. ej. muros/diques) y no estructurales (p. ej. sistema de alerta temprana, zonificación del uso de suelo en función del riesgo) con el objetivo de disminuir o mitigar el riesgo de inundación, así como para la implementación de políticas públicas que minimicen los riesgos para las poblaciones que viven en las zonas inundables y para evitar que se habiten estas zonas. Por otro lado, un estudio similar en otros tramos de este río constituiría un gran aporte para comparar los resultados de este estudio, ya sea utilizando los mismos valores de Manning establecidos por Chow (1959) o utilizando otros métodos de estimación como el utilizado por Yang et ál. (2020) a través de la implementación de un algoritmo de optimización por enjambres de partículas (PSO por sus siglas en inglés).
Conclusiones
El problema de inundaciones en el río Santa Bárbara inició recientemente un cambio significativo hacia la gestión del riesgo de inundaciones. A pesar de la escasa información disponible, el presente estudio sugiere que existe suficiente conocimiento, así como datos aceptables, para estimar la extensión de las inundaciones. Este conocimiento podría ayudar a mejorar la toma de decisiones para reducir e incluso prevenir pérdidas materiales en los ríos de montaña de la región interandina, ya que los coeficientes de Manning promedio recomendados en la literatura se pueden usar con cierto grado de confianza para la delimitación de las áreas inundables.
El uso de los niveles de crecida observados es la mejor manera de calibrar los modelos de inundación. Sin embargo, cuando estos datos no están disponibles, los gobiernos locales (p. ej los municipios) podrían obtener una línea base de áreas propensas a inundaciones, utilizando los valores promedio de Manning recomendados en la literatura para la modelación hidráulica y el mapeo de inundaciones. Las seiscientas simulaciones de MC parecen dar resultados suficientes y aceptables, lo que resulta particularmente útil en países en desarrollo, donde la información y los recursos económicos son escasos. Además, se identificó que las variaciones del coeficiente de Manning produjeron respuestas significativas en los niveles de agua, aunque no existe una variación considerable en términos de extensión de inundación. Sin embargo, la profundidad del agua es un variable importante a considerar, ya que puede poner en riesgo la vida de las personas. También, una mayor profundidad de inundación incrementa los daños económicos en la infraestructura y en los cultivos (Pinos, Orellana y Timbe 2020). En estos casos es necesario realizar una calibración precisa del coeficiente de Manning para el computo de los niveles de inundación y estimar los daños que ocasionan (p. ej. a la infraestructura y cultivos).
Los resultados también muestran que la incertidumbre en el coeficiente de Manning afecta la estimación de los niveles de inundación considerablemente (1 m. aprox.), ya que los resultados del modelo muestran diferencias sustanciales en los niveles de agua simulados.
Referencias
Referencias
Alam, Shahabul, Patrick Willems, y Masud Alam. 2014. “Comparative Assessment of Urban Flood Risks Due to Urbanization and Climate Change in the Turnhout Valley of Belgium.” ABC Journal of Advanced Research 3 (1): 14-17. https://doi.org/10.18034/abcjar.v3i1.27 DOI: https://doi.org/10.15590/abcjar/2014/v3i1/53471
Anderson, B. G., I. D. Rutherfurd, y A. W. Western. 2006. “An Analysis of the Influence of Riparian Vegetation on the Propagation of Flood Waves.” Environmental Modelling & Software 21 (9): 1290-1296. https://doi.org/10.1016/j.envsoft.2005.04.027 DOI: https://doi.org/10.1016/j.envsoft.2005.04.027
Aronica, G., P. D. Bates, y M. S. Horritt. 2014. “Assessing the Uncertainty in Distributed Model Predictions Using Observed Binary Pattern Information within Glue.” Hydrological Processes 16 (10): 2001-2016. https://doi.org/10.1002/hyp.398 DOI: https://doi.org/10.1002/hyp.398
Bladé Castellet, Ernest, Luis Cea, y Georgina Corestein. 2014. “Numerical Modelling of River Inundations.” Ingeniería del agua 18 (1): 71-82. https://doi.org/10.4995/ia.2014.3144 DOI: https://doi.org/10.4995/ia.2014.3144
Burnham, Michael W., y Darryl W. Davis. 1990. “Effects of Data Errors on Computed Steady‐Flow Profiles.” Journal of Hydraulic Engineering 116 (7): 914-929. https://doi.org/10.1061/(ASCE)0733-9429(1990)116:7(914) DOI: https://doi.org/10.1061/(ASCE)0733-9429(1990)116:7(914)
Campozano, L., D. Tenelanda, E. Sanchez, E. Samaniego, y J. Feyen. 2016. “Comparison of Statistical Downscaling Methods for Monthly Total Precipitation: Case Study for the Paute River Basin in Southern Ecuador.” Advances in Meteorology 2016: 1-13. https://doi.org/10.1155/2016/6526341 DOI: https://doi.org/10.1155/2016/6526341
Carpenter, James, y John Bithel. 2000 “Bootstrap Confidence Intervals: When, Which, What? A Practical Guide for Medical Statisticians.” Statistics in Medicine 19 (9): 1141-1164. https://doi.org/10.1002/(SICI)1097-0258(20000515)19:9%3C1141::AID-SIM479%3E3.0.CO;2-F DOI: https://doi.org/10.1002/(SICI)1097-0258(20000515)19:9<1141::AID-SIM479>3.0.CO;2-F
Chow, Ven Te. 1959. Open-Channel Hydraulics. Tokyo: McGraw-Hill Civil Engineering series.
DHI. 2001. MIKE GIS: Floodplain Mapping and Analysis, User Guide. Horsholm, Denmark: Water & Environment.
DHI. 2002. MIKE-11 A modeling system for rivers and channels reference manual. Horsholm, Denmark: Water & Environment.
Di Baldassarre, Giuliano.2012. Floods in a changing climate: inundation modelling. Vol. 3. Nueva York: Cambridge University Press. DOI: https://doi.org/10.1017/CBO9781139088411
Dimitriadis, Panayiotis, Aristoteles Tegos, Athanasios Oikonomou, Vassiliki Pagana, Antonios Koukouvinos, Nikos Mamassis, Demetris Koutsoyiannis, y Andreas Efstratiadis. 2016. “Comparative Evaluation of 1D and Quasi-2d Hydraulic Models Based on Benchmark and Real-World Applications for Uncertainty Assessment in Flood Mapping.” Journal of Hydrology 534: 478-92. https://doi.org/10.1016/j.jhydrol.2016.01.020 DOI: https://doi.org/10.1016/j.jhydrol.2016.01.020
Falter, D., N. V. Dung, S. Vorogushyn, K. Schröter, Y. Hundecha, H. Kreibich, H. Apel, F. Theisselmann, y B. Merz. 2014. “Continuous, Large-Scale Simulation Model for Flood Risk Assessments: Proof-of-Concept.” Journal of Flood Risk Management 9 (1): 3-21. https://doi.org/10.1111/jfr3.12105 DOI: https://doi.org/10.1111/jfr3.12105
Ferguson, Rob. 2010. “Time to Abandon the Manning Equation?” Earth Surface Processes and Landforms 35 (15): 1873-1876. https://doi.org/10.1002/esp.2091 DOI: https://doi.org/10.1002/esp.2091
Fread, Danny L. 1989. Flood routing models and the Manning n. Maryland: B.C. Yen, ed. Proceedings of the International Conference on Channel Flow and Catchment Runoff.
Gichamo, T. Z., I. Popescu, A. Jonoski, y D. Solomatine. 2012. “River Cross-Section Extraction from the Aster Global Dem for Flood Modeling.” Environmental Modelling & Software 31: 37-46. https://doi.org/10.1016/j.envsoft.2011.12.003 DOI: https://doi.org/10.1016/j.envsoft.2011.12.003
Hall, J. W., S. Tarantola, P. D. Bates, y M. S. Horritt. 2005. “Distributed Sensitivity Analysis of Flood Inundation Model Calibration.” Journal of Hydraulic Engineering 131(2): 117-126. https://doi.org/10.1061/(ASCE)0733-9429(2005)131:2(117) DOI: https://doi.org/10.1061/(ASCE)0733-9429(2005)131:2(117)
Hardy, R. J., P. D. Bates, y M. G. Anderson. 1999. “The Importance of Spatial Resolution in Hydraulic Models for Floodplain Environments.” Journal of Hydrology 216 (1-2): 124-136. https://doi.org/10.1016/S0022-1694(99)00002-5 DOI: https://doi.org/10.1016/S0022-1694(99)00002-5
Horritt, M. S., y P. D. Bates. 2002. “Evaluation of 1D and 2D Numerical Models for Predicting River Flood Inundation.” Journal of Hydrology 268 (1-4): 87-99. https://doi.org/10.1016/S0022-1694(02)00121-X DOI: https://doi.org/10.1016/S0022-1694(02)00121-X
Hunter, Neil M., Paul D. Bates, Matthew S. Horritt, y Matthew D. Wilson. 2007. “Simple Spatially-Distributed Models for Predicting Flood Inundation: A Review.” Geomorphology 90 (3-4): 208-225. https://doi.org/10.1016/j.geomorph.2006.10.021 DOI: https://doi.org/10.1016/j.geomorph.2006.10.021
Iooss, Bertrand, y Paul Lemaître. 2015. “A Review on Global Sensitivity Analysis Methods.” Uncertainty Management in Simulation-Optimization of Complex Systems 59: 101-22. https://doi.org/10.48550/arXiv.1404.2405 DOI: https://doi.org/10.1007/978-1-4899-7547-8_5
Jung, Younghun, Venkatesh Merwade, Kyudong Yeo, Yongchul Shin, y Seung Lee. 2013. “An Approach Using a 1D Hydraulic Model, Landsat Imaging and Generalized Likelihood Uncertainty Estimation for an Approximation of Flood Discharge.” Water 5 (4): 1598-1621. https://doi.org/10.3390/w5041598 DOI: https://doi.org/10.3390/w5041598
Lenhart, T., K. Eckhardt, N. Fohrer, y H.-G. Frede. 2002. “Comparison of Two Different Approaches of Sensitivity Analysis.” Physics and Chemistry of the Earth, Parts A/B/C 27 (9-10): 645-654. https://doi.org/10.1016/S1474-7065(02)00049-9 DOI: https://doi.org/10.1016/S1474-7065(02)00049-9
Montero, Rodolfo Alvarado, Dirk Schwanenberg, Marcus Hatz, y Martin Brinkmann. 2013. “Simplified Hydraulic Modelling in Model Predictive Control of Flood Mitigation Measures along Rivers.” Journal of Applied Water Engineering and Research 1 (1): 17-27. https://doi.org/10.1080/23249676.2013.827897 DOI: https://doi.org/10.1080/23249676.2013.827897
Mora, Diego Estebán y Patrick Willems. 2011. “Decadal Oscillations in Rainfall and Air Temperature in the Paute River Basin-Southern Andes of Ecuador.” Theoretical and Applied Climatology 108 (1-2): 267-82. https://doi.org/10.1007/s00704-011-0527-4 DOI: https://doi.org/10.1007/s00704-011-0527-4
Moussa, Roger. 1996. “Analytical Hayami Solution for the Diffusive Wave Flood Routing Problem with Lateral Inflow.” Hydrological Processes 10 (9): 1209-1227. https://doi.org/10.1002/(SICI)1099-1085(199609)10:9<1209::AID-HYP380>3.0.CO;2-2 DOI: https://doi.org/10.1002/(SICI)1099-1085(199609)10:9<1209::AID-HYP380>3.0.CO;2-2
Ochoa, A., L. Campozano, E. Sánchez, R. Gualán, y E. Samaniego. 2015. “Evaluation of Downscaled Estimates of Monthly Temperature and Precipitation for a Southern Ecuador Case Study.” International Journal of Climatology 36 (3): 1244-1255. https://doi.org/10.1002/joc.4418 DOI: https://doi.org/10.1002/joc.4418
Papaioannou, G., A. Loukas, L. Vasiliades, y G. T. Aronica. 2016. “Flood Inundation Mapping Sensitivity to Riverine Spatial Resolution and Modelling Approach.” Natural Hazards 83 (S1): 117-32. https://doi.org/10.1007/s11069-016-2382-1 DOI: https://doi.org/10.1007/s11069-016-2382-1
Pappenberger, Florian, Keith J. Beven, Marco Ratto, y Patrick Matgen. 2008. “Multi-Method Global Sensitivity Analysis of Flood Inundation Models.” Advances in Water Resources 31 (1): 1-14. https://doi.org/10.1016/j.advwatres.2007.04.009 DOI: https://doi.org/10.1016/j.advwatres.2007.04.009
Pinos, Juan, Daniel Orellana, y Luis Timbe. 2020. “Assessment of Microscale Economic Flood Losses in Urban and Agricultural Areas: Case Study of the Santa Bárbara River, Ecuador.” Natural Hazards 103: 2323-2337. https://doi.org/10.1007/s11069-020-04084-8 DOI: https://doi.org/10.1007/s11069-020-04084-8
Pinos, Juan, y Luis Timbe. 2020. “Mountain Riverine Floods in Ecuador: Issues, Challenges, and Opportunities.” Front. Water 2:545880. https://doi.org/10.3389/frwa.2020.545880 DOI: https://doi.org/10.3389/frwa.2020.545880
SENAGUA (Secretaria Nacional del Agua). 2014. “Análisis de la vulnerabilidad a eventos de crecida y diseño de obras físicas para la protección de márgenes e infraestructura del río santa bárbara.” 2014. Vol. 2. Cuenca: Estudio Hidráulico, Demarcación Hidrográfica del Santiago.
Tayefi, V., S. N. Lane, R. J. Hardy, y D. Yu. 2007. “A Comparison of One- and Two-Dimensional Approaches to Modelling Flood Inundation over Complex Upland Floodplains.” Hydrological Processes 21 (23): 3190-3202. https://doi.org/10.1002/hyp.6523 DOI: https://doi.org/10.1002/hyp.6523
Timbe, Luis M. 2007. River Flooding Analysis Using Quasi-2D Hydraulic Modelling and Geospatial Data. Heverlee: Katholieke Universiteit Leuven.
Weichel, T., F. Pappenberger, y Karsten Schulz. 2007. “Sensitivity and Uncertainty in Flood Inundation Modelling - Concept of an Analysis Framework.” Advances in Geosciences 11: 31-36. https://doi.org/10.5194/adgeo-11-31-2007 DOI: https://doi.org/10.5194/adgeo-11-31-2007
Willems, P. 2012. “Model Uncertainty Analysis by Variance Decomposition.” Physics and Chemistry of the Earth, Parts A/B/C 42-44: 21-30. https://doi.org/10.1016/j.pce.2011.07.003 DOI: https://doi.org/10.1016/j.pce.2011.07.003
Wohl, Ellen E. 1998. “Uncertainty in Flood Estimates Associated with Roughness Coefficient.” Journal of Hydraulic Engineering 124 (2): 219-223. https://doi.org/10.1061/(ASCE)0733-9429(1998)124:2(219) DOI: https://doi.org/10.1061/(ASCE)0733-9429(1998)124:2(219)
Wong, Jefferson S., Jim E. Freer, Paul D. Bates, David A. Sear, y Elisabeth M. Stephens. 2014. “Sensitivity of a Hydraulic Model to Channel Erosion Uncertainty during Extreme Flooding.” Hydrological Processes 29 (2): 261-79. https://doi.org/10.1002/hyp.10148 DOI: https://doi.org/10.1002/hyp.10148
Yadaicela, Julio A. 2012. “Estudio técnico sobre la implementación de generación distribuida en el sistema eléctrico ecuatoriano.” Tesis de Ingeniería Eléctrica, Escuela Politécnica Nacional, Quito.
Yang, Fan, Jingxiu Wu, Yu Zhang, Senlin Zhu, Guoqing Liu, Guangyu Chen, Shiqiang Wu, y Ziwu Fan. 2020. “Improved Method for Identifying Manning’s Roughness Coefficients in Plain Looped River Network Area.” Engineering Applications of Computational Fluid Mechanics 15 (1): 94-110. https://doi.org/10.1080/19942060.2020.1858967 DOI: https://doi.org/10.1080/19942060.2020.1858967
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2023 Autor - Revista
Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
Cuadernos de Geografía: Revista Colombiana de Geografía es publicada por la Universidad Nacional de Colombia y está licenciada bajo los términos de Creative Commons Reconocimiento-NoComercial-SinObraDerivada 4.0 Internacional License.
