Análisis de los factores de riesgo en el seguro de automóvil mediante ecuaciones estructurales

ANALYSIS OF RISK FACTORS IN CAR INSURANCE THROUGH STRUCTURAL EQUATIONS

La gestión de riesgos, asociada al seguro del automóvil, es una cuestión crucial a la que se enfrentan en la actualidad tanto actuarios como profesionales del sector. Es clave seleccionar adecuadamente los factores de riesgos para asignar las tarifas a los asegurados en función del riesgo asociado. Por tanto, el objetivo de este trabajo es comprobar empíricamente la validez de la utilización de los niveles de "bonus-malus" para clasificar adecuadamente a los asegurados a través de dos modelos de ecuaciones estructurales. Los análisis sobre una muestra de 4.365 pólizas automovilísticas españolas descritas a través de 11 factores de riesgo muestran que la variable BM contribuye a mejorar la capacidad explicativa del modelo pero no de manera significativa.

Risk management, associated to car insurance, is a crucial issue currently faced by both actuaries and field professionals. It is essential to adequately choose the risk factors to assign the payment rates to policyholders according to the associated risks. Therefore, the purpose of this work is to demonstrate, in an empirical way, the validity of using "bonus malus" (BM) levels to classify policyholders correctly through two models of structural equations. The analysis of a sample of 4,365 Spanish car insurance policies described through 11 risk factors shows that the variable BM contributes to improving the explaining capacity of the model, though not in a significant way.

A gestão de riscos, associada com o seguro do automóvel, é uma questão crucial à qual se enfrentam, na atualidade, tanto atuários quanto profissionais do setor. É fundamental selecionar adequadamente os fatores de riscos para designar as tarifas aos segurados em função do risco associado. Portanto, o objetivo deste trabalho é comprovar empiricamente a validade da utilização dos níveis de bonus-malus (BM) para classificar adequadamente os segurados por meio de dois modelos de equações estruturais. As análises sobre uma amostra de 4.365 apólices automobilísticas espanholas descritas por meio de 11 fatores de risco mostram que a variável BM contribui para a melhoria da capacidade explicativa do modelo, mas não de maneira significativa.

DOI: https://doi.org/10.15446/innovar.v25n1spe.53369.

Análisis de los factores de riesgo en el seguro de automóvil mediante ecuaciones estructurales¹

ANÁLISE DOS FATORES DE RISCO NO SEGURO DE AUTOMÓVEL MEDIANTE EQUAÇÕES ESTRUTURAIS

ANALYSE DES FACTEURS DE RISQUE POUR L'ASSURANCE AUTOMOBILE PAR ÉQUATIONS STRUCTURELLES

María Jesús Segovia-Vargas^*, María-del-Mar Camacho-Miñano^**, David Pascual-Ezama^***, Piedad Tolmos Rodríguez-Piñero^****

^* Ph.D. en Ciencias Económicas y Empresariales Universidad Complutense de Madrid Madrid, España. Riesgo en Seguros y Finanzas (UCM)
Correo electrónico: mjsegovia@ccee.ucm.es
^**Ph.D. en Ciencias Económicas y Empresariales University College for Financial Studies (CUNEF) Madrid, España INIFCO-UCM (UCM)
Correo electrónico: marcamacho@cunef.edu
^*** Ph.D. en Psicología. Universidad Complutense de Madrid. Madrid, España. INIFCO-UCM (UCM)
Correo electrónico: david.pascual@ccee.ucm.es
^**** Ph.D. en Ciencias Económicas y Empresariales Universidad Rey Juan Carlos Madrid, España
Correo electrónico institucional: piedad.tolmos@urjc.es

¹ Este trabajo fue parcialmente financiado por el Ministerio de Ciencia e Innovación de España por el proyecto: ref. ECO2010-22065-C03-01.

Correspondencia Dra. María Jesús Segovia Vargas. Facultad de Ciencias Económicas y Empresariales. Universidad Complutense de Madrid. Campus de Somosaguas. Edificio 5. Despacho 109. 28223 Pozuelo de Alarcón. Madrid, España.

Citación: Segovia-Vargas, M. J., Camacho-Miñano, M. del M., Pascual-Ezama, D., & Tolmos Rodríguez-Piñero, P. (2015). Análisis de los factores de riesgo en el seguro de automóvil mediante ecuaciones estructurales. Innovar, Edición Especial2015, 121-130. doi: 10.15446/innovar.v25n1spe.53369.

Clasificación JEL: C44, D19, G22.

Recibido: Abril 2012, Aprobado: Febrero 2015.

---

RESUMEN: La gestión de riesgos, asociada al seguro del automóvil, es una cuestión crucial a la que se enfrentan en la actualidad tanto actuarios como profesionales del sector. Es clave seleccionar adecuadamente los factores de riesgos para asignar las tarifas a los asegurados en función del riesgo asociado. Por tanto, el objetivo de este trabajo es comprobar empíricamente la validez de la utilización de los niveles de "bonus-malus" para clasificar adecuadamente a los asegurados a través de dos modelos de ecuaciones estructurales. Los análisis sobre una muestra de 4.365 pólizas automovilísticas españolas descritas a través de 11 factores de riesgo muestran que la variable BM contribuye a mejorar la capacidad explicativa del modelo pero no de manera significativa.

PALABRAS CLAVE: Factores de riesgo, seguro del automóvil, sistema bonus-malus, ecuaciones estructurales.

---

ABSTRACT: Risk management, associated to car insurance, is a crucial issue currently faced by both actuaries and field professionals. It is essential to adequately choose the risk factors to assign the payment rates to policyholders according to the associated risks. Therefore, the purpose of this work is to demonstrate, in an empirical way, the validity of using "bonus malus" (BM) levels to classify policyholders correctly through two models of structural equations. The analysis of a sample of 4,365 Spanish car insurance policies described through 11 risk factors shows that the variable BM contributes to improving the explaining capacity of the model, though not in a significant way.

KEYWORDS: Risk factors, car insurance, bonus-malus system, structural equations.

---

RESUMO: A gestão de riscos, associada com o seguro do automóvel, é uma questão crucial à qual se enfrentam, na atualidade, tanto atuários quanto profissionais do setor. É fundamental selecionar adequadamente os fatores de riscos para designar as tarifas aos segurados em função do risco associado. Portanto, o objetivo deste trabalho é comprovar empiricamente a validade da utilização dos níveis de bonus-malus (BM) para classificar adequadamente os segurados por meio de dois modelos de equações estruturais. As análises sobre uma amostra de 4.365 apólices automobilísticas espanholas descritas por meio de 11 fatores de risco mostram que a variável BM contribui para a melhoria da capacidade explicativa do modelo, mas não de maneira significativa.

PALAVRAS-CHAVE: Fatores de risco, seguro do automóvel, sistema de bonus-malus, equações estruturais.

---

RÉSUMÉ: La gestion des risques associés à l'assurance du véhicule est une question cruciale que les actuaires comme les professionnels du secteur confrontent actuellement. Il est essentiel de bien choisir les facteurs de risque pour attribuer les tarifs aux assurés en fonction du risque associé. Par conséquent, le but de cet article est de tester empiriquement la validité de l'utilisation des niveaux de "bonus-malus" afin de classer correctement les assurés à travers deux modèles d'équations structurelles. Les analyses d'un échantillon de 4.365 polices d'assurance automobile espagnoles, décrites par 11 facteurs de risque, montrent que la variable BM contribue à améliorer le pouvoir explicatif du modèle, mais pas de manière significative.

MOTS CLÉS: Facteurs de risque, assurance automobile, système de bonus-malus, équations structurelles.

---

Problemática actual del seguro automovilístico

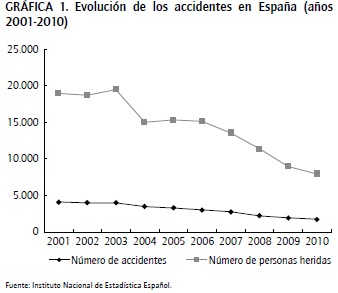
Las compañías de seguros intentan clasificar sus pólizas en clases tarifarias homogéneas, es decir, asignando a las mismas todas aquellas pólizas que pertenezcan a la misma clase. De este modo, se consigue cobrar una prima adecuada (justa) a los conductores. Según comenta Arvidsson (2010), "la precisión es algo crucial". Existen dos razones por las que es extremadamente importante para una aseguradora seleccionar un conjunto adecuado de factores de riesgo que contribuyan a predecir de manera correcta las futuras tasas de siniestralidad. En primer lugar, la competencia en el mercado de seguros está aumentando en la actualidad, sobre todo debido a las ofertas especiales de las empresas por internet (Segovia-González, Contreras y Mar-Molinero, 2009). En segundo lugar, la tasa de accidentes ha descendido de manera significativa en la última década, especialmente en España, con una reducción del 50% (el descenso en el número de accidentes y personas heridas puede verse en la Gráfica 1). Debido a estas circunstancias, la prima por siniestralidad podría reajustarse de manera efectiva, dado que la probabilidad de una indemnización muy alta ha descendido.

Sin embargo, dicho reajuste debe estar limitado por las aseguradoras por razones de viabilidad económica, ya que podría conducir en un caso extremo a la insolvencia. En consecuencia, se necesita una convergencia en las empresas aseguradoras entre un posible reajuste en la prima del seguro y el fomento de la estabilidad financiera. De hecho, la nueva regulación Solvencia II, relativa a la solvencia de las compañías aseguradoras en el ámbito de la Unión Europea, ha supuesto la revisión de las normas de evaluación de la situación financiera de dichas entidades. El objetivo de la nueva normativa es mejorar la medición y control del riesgo con el fin último de proteger a los tomadores de seguros. Para ello, las entidades aseguradoras deben disponer de un nivel de recursos propios ajustado al riesgo real asumido por las mismas. Para cumplir los objetivos propuestos, Solvencia II (al igual que Basilea II para las entidades financieras) se articula en tres pilares: pilar I, referido a los requerimientos cuantitativos; pilar II, referido a los requerimientos cualitativos, y pilar III o de disciplina de mercado (Directiva 2009/138/CE).

Si nos centramos en el primer pilar, su objetivo es determinar el "Balance Económico" enfocado al riesgo propio de la entidad y valorado a mercado mediante normas establecidas para la valoración de los activos y pasivos con los que cuentan las entidades aseguradoras. Para cumplir con estos requisitos, es necesario que, primeramente, las entidades aseguradoras establezcan y definan las reglas de valoración que seguirán para cuantificar todas las partidas relevantes del balance económico, tanto del activo como del pasivo. Dicha valoración se deberá realizar en conjunto y conducirá a un imagen fiel del balance (sin sobrevalora-ción del activo ni infravaloración del pasivo) de tal forma que se puedan obtener los niveles de capital adecuados al perfil de riesgos asumidos por la entidad, lo que redundará en una mayor solidez del sector asegurador en particular y de la economía en general. Por lo tanto, Solvencia II requiere, de manera explícita, la investigación de la correlación del comportamiento del tomador de una póliza con los factores de riesgo de la misma, para así ajustar su balance económico. En línea con esta nueva regulación, la profundiza-ción en los factores de riesgo, en concreto del seguro del automóvil, mejorará la estimación de la siniestralidad para dicho ramo y permitirá a las compañías ajustar su capital al nivel de riesgo real en el que incurren, sin que la protección de los asegurados se vea mermada.

Debemos mencionar que la prima pagada en un seguro de coche depende de la clase a la cual se ha asignado al conductor principal. Esta asignación tiene claras consecuencias para las dos partes, que se ven afectadas por la elección del sistema de clasificación: para la aseguradora, debido a los gastos e ingresos en los que incurre, y para el conductor asegurado, debido al precio de la prima que paga.

La política de clasificación se basa en los denominados factores de riesgo. Estos factores son característicos de las pólizas y ayudan a las compañías a estimar las posibles cantidades por indemnización en un periodo de tiempo dado (generalmente un año). En el seguro de automóvil, estos factores son características observables relativas al conductor, al vehículo y al tráfico. Las principales variables clasificatorias usadas en la industria del seguro del automóvil son las siguientes: edad del conductor, género, registro de accidentes o reclamaciones del conductor principal, año de obtención del carné de conducir, tipo de vehículo y lugar de residencia. Estas variables observables o medibles objetivamente podrían marcar las diferencias entre los diferentes conductores como el género, la edad o la experiencia. Por ejemplo, hay estudios empíricos que muestran que los hombres tienen dos veces más de probabilidades de tener, al menos, un accidente como conductor que las mujeres, y casi tres veces más probabilidades de tener dos o más accidentes. Además, los conductores de entre 17 y 29 años tienen dos veces más probabilidad de tener al menos un accidente que las personas mayores de 50 años (Glendon, Dorn, Davies, Matthews y Taylor, 1996).

El modo habitual para seleccionar los factores de riesgo se basa en técnicas estadísticas de análisis multivariante. Aunque estas técnicas todavía dejan una gran cantidad de heterogeneidad dentro de las clases tarifarias, hay literatura científica relativa a la cuestión de la clasificación de riesgos de los aseguradores (Arvidsson, 2010; Denuit, Maréchal, Pitrebois y Walhin, 2007). Sin embargo, a la hora de tarificar los seguros de automóviles hay importantes factores que no pueden ser considerados a priori, como por ejemplo: la rapidez de reflejos o el comportamiento agresivo al volante. Estudios previos muestran como otras variables como la agresividad, la personalidad, el estrés o la propensión al riesgo deberían tenerse en cuenta y, sin embargo, al menos de forma explícita, no parece que las compañías les den mucha importancia. Por ejemplo, cuando se tiene en cuenta la propensión al riesgo, el número de accidentes que tienen los hombres o aquellos con edades comprendidas entre 17 y 29 años de edad disminuye sus-tancialmente (Turner y McClure, 2003). Por otro lado, la personalidad es una variable muy importante en la predicción de accidentes de coches (Schewebel, Severson, Ball y Rizzo, 2006). Si observamos las distintas escalas de personalidad, existen algunas como la agresividad que están directamente asociadas con comportamientos de conducción de riesgo y, por lo tanto, con riesgo de accidente (Gulliver y Begg, 2007). Por último, el estrés del conductor también se correlaciona con la probabilidad de tener un accidente, ya que está relacionado con otras variables como peor percepción, falta de atención o estado de ánimo (Matthews, Dorn y Glendon, 1991). Estas variables están correlacionadas con las tasas de siniestralidad y, por lo tanto, pueden utilizarse para predecir futuros siniestros. De hecho, los psicólogos han demostrado que los accidentes de carretera están relacionados con el comportamiento de los conductores (Aberg y Rimmó, 1998) y con las infracciones de tráfico (Arvidsson, 2010; Forward, 2008). Por lo tanto, se considera que estas "características escondidas" o "factores escondidos" son reveladas, solo en parte, por el número de siniestros acreditados por los asegurados (Pitrebois, Denuit y Walhin, 2006). Luego, la prima puede reajustarse de acuerdo con el número de siniestros de los que han informado los asegurados. Esto se hace normalmente integrando el historial relativo a los siniestros pasados en el denominado sistema "bonus-malus" (BM). De este modo, el sistema BM es un sistema de ajustes de la prima a pagar por el asegurado basado en bonificaciones (cuanto menos siniestros, más barata es la prima) y en pe-nalizaciones (cuantos más siniestros, más cara es la prima). El objetivo de este sistema tiene un doble propósito: animar a los asegurados a conducir más cuidadosamente y lograr una mejor valoración de los riesgos individuales, de tal modo que todo el mundo pague una prima de acuerdo a su historial de frecuencia de siniestros (Lemaire, 1988). Sin embargo, es relevante destacar que el sistema de BM no se utiliza en todos los países, fundamentalmente debido a dos factores: la madurez del mercado asegurador y la cultura nacional (Park, Lemaire y Chua, 2009).

En este contexto, queremos destacar que los esquemas basados en el sistema BM "fuerzan" a los asegurados a decidir si la magnitud del siniestro es lo suficientemente importante para justificar un parte, ya que una reclamación (un parte) necesariamente implica una pérdida futura de bonificación en muchos casos. Por tanto, los asegurados pueden tener información no observable para el asegurador que prediga el riesgo ex-post (Arvidson, 2010). Hay evidencia empírica demostrada que señala que "los conductores que están involucrados en accidentes de tráfico en el último año asumen más riesgos al conducir" (Iversen, 2004, p. 147). Sin embargo, mientras continúa el debate sobre los efectos, ventajas y desventajas sobre los sistemas BM, su uso puede aumentar la eficiencia del mercado (Heras, Vilar y Gil, 2002; Hey, 1985; Richaudeau, 1999).

Cuando se aplica un sistema BM, la prima se calcula multiplicando la prima original por un porcentaje que se le asigna al asegurado según sea su posición en la escala del BM. Este porcentaje es el denominado coeficiente bonus-malus. Por lo tanto, el sistema de BM "afina" o ajusta la clasificación tarifaria efectuada a priori. Es decir, el sistema de BM redefine a posteriori la tarificación efectuada a priori (Dionne y Ghali, 2005; Pitrebois et al., 2006). Esta asignación es esencial desde el punto de vista financiero, porque si los asegurados con más riesgo están mal clasificados en la escala del BM, la compañía podría incurrir en costes y riesgos muy altos. Tal situación podría poner en peligro el futuro de la aseguradora. En consecuencia, consideraremos en nuestro estudio otra variable, el nivel de BM, junto con los factores de riesgo originales.

Con todas estas premisas, el objetivo de nuestro trabajo es comprobar la capacidad de explicación de los factores de riesgo considerados sobre la variable "accidente" sin considerar la variable BM, y posteriormente considerando la variable BM. Para ello desarrollaremos dos modelos: uno que contiene únicamente los factores de riesgo originales y otro que considere estos factores junto con los niveles de BM. Finalmente, compararemos la capacidad explicativa de ambos modelos tratando de analizar si la variable BM añade información que mejore la clasificación tarifaria de las pólizas en el seguro de coche. Esto se conseguiría si esta variable explicara de manera suficiente los denominados "factores ocultos" y permitiría una asignación de precios más precisa. Si el modelo con la variable BM mejora de manera significativa la explicación de la variable accidente (siniestralidad) en relación al modelo que no incluye dicha variable, podríamos concluir que los "factores o características ocultas" son explicados suficientemente por esa variable.

La principal contribución de nuestro estudio es que demostramos empíricamente que el sistema bonus-malus para clasificar los riesgos de los conductores de automóviles mejora la explicación de la variable accidente, aunque no significativamente. Se formulan nuevas propuestas para ajustar de manera más precisa las primas de los asegurados, sin poner en peligro la viabilidad financiera de las empresas aseguradoras.

El artículo se divide en las secciones siguientes: en la segunda sección se muestran los datos y variables empleados así como la metodología en que se basan las ecuaciones estructurales que hemos empleado para desarrollar los dos modelos; en la tercera, se muestran los resultados, es decir, los dos modelos desarrollados; en la cuarta, se incluye la discusión de los mismos y, finalmente, terminamos con una quinta sección en la que se explican las conclusiones del estudio y propuestas de mejora.

Muestra y metodología

Datos y selección de las variables

Para la parte empírica se ha utilizado una muestra de 4.365 pólizas españolas referidas al año 2005. Los datos han sido proporcionados por una de las grandes compañías aseguradoras de nuestro país (España).

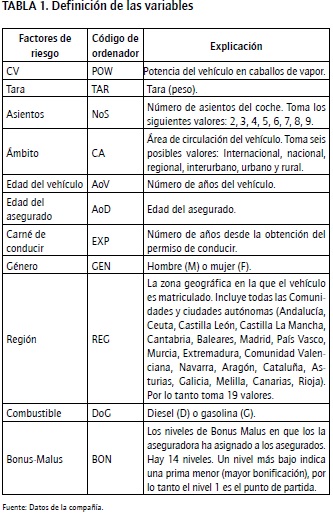
Los factores de riesgo (variables) utilizados por la aseguradora son los habitualmente usados por el sector y constituyen una mezcla tanto de variables cualitativas como cuantitativas (Tabla 1). Hemos de mencionar que en este trabajo se ha centrado únicamente en pólizas suscritas por individuos que conducen su propio automóvil para su uso personal, aunque la compañía también asegura otros tipos de vehículos (tanto públicos como privados y para otros usos).

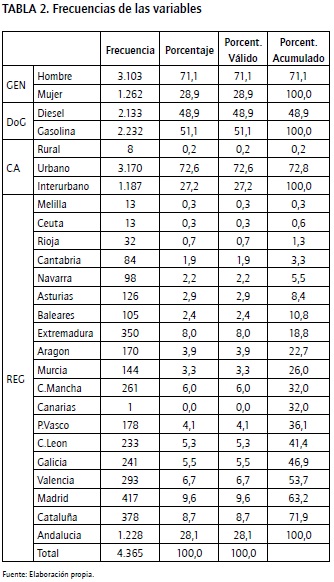
De acuerdo con la Tabla 2, la muestra se compone principalmente por hombres (71,1%), con aproximadamente la mitad de coches diesel y la mitad gasolina. El 98% de los coches se mueven en el ámbito urbano o interurbano con casi un 30% de los mismos circulando por la comunidad andaluza, en el sur de España.

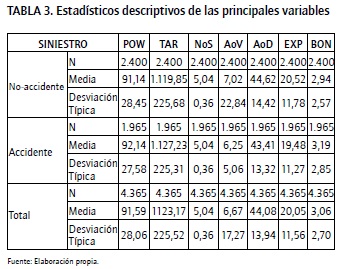
Otra información importante de la muestra (Tabla 3) es que los coches tienen 5 asientos de media y 6,7 años de antigüedad, con una potencia media de algo más de 90 caballos y un peso medio de 1.123 kilos. La edad media de los conductores es 44, con una experiencia media de 20 años.

Las pólizas se clasifican en dos categorías: accidente (A) o no-accidente (N_A). Es importante resaltar que los asegurados se asignan a dichas categorías teniendo en cuenta los siniestros acreditados y no su cuantía (es decir, cuando se da un parte, el asegurado es reclasificado a la clase "accidente"). Esto es debido a que la mayoría de los sistemas bonus-malus en vigor (con muy pocas excepciones como Korea) penalizan solo el número de siniestros (Lemaire, 1995). Este hecho conduciría a que la clase "accidente" fuese muy heterogénea, pero no es así ya que se vuelve más homogénea por la utilización que hace la aseguradora de los catorce niveles de bonus-malus.

Procedimiento

Con el objetivo de analizar el impacto de la variable BM en la tarificación de los seguros de automóviles, se han aplicado dos modelos de ecuaciones estructurales basados en las variables observadas (Path Analysis). Un primer modelo explica la probabilidad de que el asegurado tenga un siniestro, teniendo en cuenta las variables utilizadas normalmente por las aseguradoras y un segundo modelo en el que se incluya una variable surgida de la experiencia del asegurado con su automóvil denominada BM. El motivo por el que decidimos utilizar un modelo de ecuaciones estructurales es porque constituye una de las herramientas más potentes para el estudio de relaciones causales cuando estas relaciones son de tipo lineal (López, Fernández y Mariel, 2002). Los modelos de ecuaciones estructurales analizan las relaciones causales y no causales entre los diferentes constructos que forman parte del modelo, sin tener en cuenta el error de medida en el proceso de análisis. A partir de una base teórica previa, el modelo diseñado tiene como objetivo representar las variables latentes y la relación existente entre las mismas. Dentro de los modelos de ecuaciones estructurales, uno de los más utilizados es el "path analysis". El "path analysis" es un análisis causal cuyo objetivo es el estudio de los efectos de unas variables consideradas como causas sobre otras tomadas como efectos (Casas, 2002). La variable que es efecto se denomina variable dependiente, endógena o explicada, y las que originan la anterior son las variables independientes, exógenas o explicativas. El "path analysis" es una técnica similar a la regresión (Figura 1) pero con mayor poder explicativo, que estudia los efectos directos e indirectos en el conjunto de las variables observables, asumiendo la existencia de relaciones lineales entre ellas, la ausencia de correlación de los errores de regresión y la ausencia de errores de medición de las variables (Altoè, 2008). De hecho, puede haber interrelaciones entre algunas variables que no sean observables con relaciones lineales y sí con "path analysis".

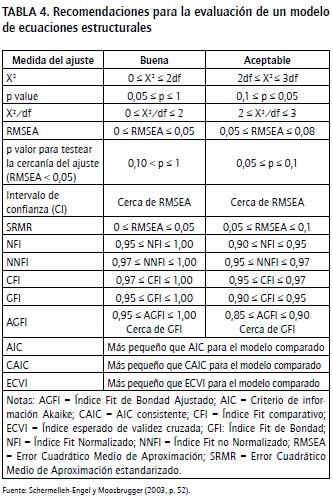
La bondad del modelo y su adecuación viene marcada por los índices "fit", como requisito previo a la medición de la capacidad explicativa del modelo. Para todos estos análisis se ha utilizado el paquete estadístico LISREL 8.7 y para la matriz de correlaciones la función PRELIS (Jóreskog y Sórbom, 1993). Siguiendo las recomendaciones de Hu y Bentler (1995), la bondad del modelo fue evaluada por medio de varios índices. Adicionalmente al Chi-cuadrado, se ha usado también el índice de Chi-cuadrado dividido por los grados de libertad, que es sensible al tamaño de la muestra. Para estos índices, valores por debajo de 3 podrían ser considerados satisfactorios (Bollen y Long, 1993). Otros índices utilizados son: el RMSEA (Root Mean Square Error of Approximation), el GFI (Goodness of Fit Index), el CFI (Comparative Fit Index), el NFI (Normed Fit Index) y el NNFI (Nonnormed Fit Index). Para el RMSEA, valores por debajo de 0,05 se considerarían buenos resultados y valores entre 0,05 y 0,08 se considerarían aceptables. Valores por encima de 0,08 nos indicarían errores de aproximación a la población (Browne y Cudeck, 1992). El GFI debería estar por encima de 0,90 (Bentler, 1992), al igual que el NFI y el CFI, para que se considerase un buen modelo. Otros autores (Schermelleh-Engel y Moosbrugger, 2003) son más exigentes y consideran aceptables algunos de los índices solamente por encima de 0,95 (Tabla 4). El cumplimiento de estos índices indica la bondad del modelo y su adecuación, y son un requisito previo a la medición de la capacidad explicativa del modelo. Finalmente los índices AIC y CAIC nos sirven para comparar varios modelos entre sí y decidir el mejor de ellos. Serán mejores aquellos modelos que tengan unos menores índices AIC y CAIC.

Resultados

Los resultados obtenidos mediante el análisis de ecuaciones estructurales en el primer modelo en el que el BM no está incluido muestran que el poder explicativo del mismo es alto, ya que la R² del modelo es 0,84. Al igual que en cualquier modelo de regresión, los valores aceptables para la R² son aquellos superiores al 80% (Cohen, Cohen, West y Aiken, 2002); es decir, el modelo puede explicar correctamente la variable dependiente (Figura 2).

Los análisis de ecuaciones estructurales nos ofrecen un valor de chi-cuadrado de 6 con 9 grados de libertad. Los indicadores FIT analizados nos muestran una alta adecuación del modelo (CFI = 1; NFI = 1; GFI = 0,98; p < 1). Además el Root Mean Square Residual y el RMSEA fueron 0,000. Los índices AIC y CAIC son de 136,02 y 637,95, respectivamente.

Se obtienen resultados similares si repetimos los análisis incluyendo esta vez en el modelo la variable BM (Figura 3). El poder explicativo de este modelo también es alto (R² = 0,86).

Los análisis de ecuaciones estructurales nos ofrecen un valor de chi-cuadrado de 6,19 con 10 grados de libertad. Los indicadores FIT analizados nos muestran una alta adecuación del modelo (CFI = 1; NFI = 1; GFI = 0,96; p < 0,8). Además el Root Mean Square Residual y el RMSEA son 0,000. El modelo con BM tiene un índice AIC de 114 y CAIC de 534,74.

Para ambos modelos, las variables explicativas de la probabilidad de siniestro son adecuadas ya que ambos modelos son buenos. Esto viene avalado por el fuerte poder explicativo que tienen para la predicción de siniestros. El primer modelo, en el que no se incluye la variable BM, tiene una capacidad predictiva sobre los siniestros del 84%. El segundo modelo, en el que se incluye la variable BM, aumenta su capacidad explicativa hasta el 86%. Por lo tanto, la inclusión de la variable BM incrementa el poder explicativo del modelo en un 2%. Además, los índices AIC y CAIC son menores en el modelo en el que se incluye el BM, por lo que el modelo es más robusto al incluir esta variable.

Conclusiones

Las empresas de seguros de automóviles, cuando tienen que tarificar o clasificar a los conductores en función del riesgo de tener un accidente para calcular la prima a pagar por cada uno de ellos, utilizan una serie de factores observables que se ha comprobado que están correlacionados con dicho riesgo. Sin embargo, hay otra serie de factores "no observables" que podrían ajustar dicha tarificación y que las compañías de seguros no miden directamente. Teóricamente se supone que dichas variables deberían estar reflejadas en el BM, ya que como hemos dicho anteriormente los "factores escondidos" son revelados, en parte, por el número de siniestros acreditados por los asegurados (Pitrebois et al., 2006) y la prima puede reajustarse de acuerdo con el número de siniestros de los que han informado los asegurados. Esto se hace normalmente integrando el historial relativo a los siniestros pasados en el denominado "sistema bonus-malus". Por lo tanto y teniendo en cuenta todo lo anterior, un modelo en el que se incluye el BM debería ser sustancialmente mejor que aquel modelo en el que no se incluya dicho concepto. Por eso el objetivo de este artículo ha sido comprobar la capacidad de explicación de los factores de riesgo considerados sobre la variable "accidente" sin considerar la variable BM, y posteriormente considerando la variable BM.

Los resultados muestran que ambos modelos son satisfactorios debido a que la capacidad explicativa de ambos modelos es superior al 80%, tal y como sugieren Cohen et al. (2002). La inclusión del BM en el modelo aumenta el poder explicativo del modelo en un 2% en consonancia con algunos resultados basados en métodos de clasificación utilizando métodos de inteligencia artificial como Bousoño, Heras y Tolmos (2008). La inclusión de la variable BM, aunque mejora la explicación del modelo, no lo hace en gran medida y, por lo tanto, no recoge suficientemente los "factores ocultos" en sintonía con los resultados encontrado hace varios años por Hey (1985). No obstante, si bien consideramos que un 2% de incremento en la capacidad explicativa del modelo no representa la importancia que estos "factores escondidos" tienen en el comportamiento de los conductores, hay que aclarar que la capacidad explicativa antes de la inclusión del BM ya era muy alta y, por tanto, es difícil incrementar sustancialmente la misma.

Por este motivo, proponemos otra serie de mediciones directas de las variables psicológicas mencionadas anteriormente que a priori pudieran parecer muy relevantes para poder incrementar la capacidad explicativa de que ocurra un accidente. Alguna sugerencia sería la utilización de cuestionarios que podrían ser utilizados para medir las características "ocultas". En concreto, en España los conductores deben renovar su permiso de conducir cada cierto tiempo. Esto requiere un examen médico que garantice las condiciones físicas para conducir, pero nuestra propuesta es que también podría ser utilizado para medir los factores psicológicos mencionados anteriormente utilizando, por ejemplo, el "Inventario de Comportamiento de conducción" para la conducción de estrés (Gulian, Matthews, Glendon, Davies y Debney, 1989), el "NEO-FFI" de personalidad (Costa y McCrae, 1992), el "Zuckerman-Kuhlman de cinco factores" para la tendencia a asumir riesgos relacionados con la personalidad (Zuckerman y Kuhlman, 2000) o un nuevo cuestionario sencillo con una mezcla de cuestionarios tradicionales. Otra sugerencia sería tener en cuenta el "sistema de puntos del carné de conducir" que se utiliza en algunos países europeos como Reino Unido, Alemania, Francia, Italia, Irlanda, Luxemburgo o España, como un proxy para mejorar la predicción de que surja un accidente.

En resumen, existen muchas variables importantes que podrían incrementar la probabilidad de predecir accidentes y que no son tenidas en cuenta de forma directa. Según los resultados encontrados en este trabajo no parece que la BM recoja todas estas variables o al menos no recoge la importancia que estas variables tienen. Por lo tanto, consideramos que se deberían incrementar el número de pruebas a efectuar a los conductores para poder realizar una medida directa de estos "factores ocultos" que hasta ahora no han recibido la atención que corresponde con su importancia.

---

Referencias bibliográficas

Altoé, G. (2008). Introduzione all'utilizzo dei modelli di equazioni strut-turali in psicologia cross-culturale. Corso di Psicologia Culturale dello Sviluppo. Padova: Universitá degli Studi di Padova - Facoltá di Psicologia.

Arvidsson, S. (2010). Does private information affect the insurance risk? Working paper, The Geneva Association, 396. Disponible en: http://swopec.hhs.se/vtiwps/abs/vtiwps2010_001.htm.

Áberg, L., & Rimmó, P. A. (1998). Dimensions of aberrant behavior. Ergonomics, 41, 39-56.

Bentler, P. M. (1992). On the fit of models to covariances and methodology to the Bulletin. Psychological Bulletin, 112, 400-404.

Bollen, K. A., & Long, J. S. (1993). Testing structural equation models. Newbury Park, CA: Sage.

Browne, M. W., & Cudeck, R. (1992). Alternative ways of assessing model fit. Sociological Methods and Research, 21, 230-258.

Bousoño, C., Heras, A., & Tolmos, P. (2008) Factores de Riesgo y Cálculo de Primas mediante Técnicas de Aprendizaje. Madrid: Editorial MAPFRE.

Casas, M. (2002). Los modelos de ecuaciones estructurales y su aplicación en el índice europeo de satisfacción del cliente. Rect@. ASEPUMA, 10(1), 1-27.

Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2002). Applied Multiple Regression/Correlation Analysis for the Behavioural Sciences. New Jersey: Routledge, Lawrence Erlbaum Associates, Inc. Publishers, 3^a edición.

Costa, P. T. Jr., & McCrae, R. R. (1992). NEO PI-R professional manual. Odessa, FL: Psychological Assessment Resources, Inc.

Denuit, M., Maréchal, X., Pitrebois, S., & Walhin, J. F. (2007). Actuarial Modelling of Claim Counts: Risk Classification, Credibility and Bonus-Malus Systems. UK: John Wiley & Sons, Ltd.

Dionne, G., & Ghali, O. (2005). The Bonus-Malus System in Tunisia: An empirical Evaluation. Journal of Risk and Insurance, 72(4), 60 9-633.

Directiva 2009/138/CE del Parlamento Europeo y del Consejo, de 25 de noviembre de 2009, sobre el seguro de vida, el acceso a la actividad de seguro y de reaseguro y su ejercicio (Solvencia II). Disponible en: http://eur-lex.europa.eu/legal-content/ES/ALL/;ELX_SESSIONID=FMVYTP9YyFV5pvvmnKrDJ5JD2XRQz6TTpnm5Vy7GZQJcyT0x 6kJ8!337030866?uri=CELEX:32009L0138.

Forward, S. (2008). Driving violations: investigating forms of irrational rationality. Uppsala: Universitetsbiblioteket. Disponible en: http://uu.diva-portal.org/smash/get/diva2:172720/FULLTEXT01.

Glendon, A. I., Dorn, L., Davies, D. R., Matthews, G., & Taylor, R. G. (1996). Age and Gender Differences in Perceived Accident Likelihood and Driver Competences. Risk Analysis, 16, 755-762.

Gulian, E., Matthews, G., Glendon, A. I., Davies, D. R., & Debney, L. M. (1989). Dimensions of driver stress. Ergonomics, 32, 585-602.

Gulliver, P., & Begg, D. (2007). Personality factors as predictors of persistent risky driving behavior and crash involvement among young adults. Injury Prevention, 13(6), 376-381.

Heras, A., Vilar, J. L., & Gil, J. A. (2002). Asymptotic Fairness of Bonus-Malus systems and Optimal Scales Premiums. The Geneva Papers on Risk and Insurance Theory, 27, 61-82.

Hey, J. (1985). No claim bonus? The Geneva Papers on Risk and Insurance Theory, 10, 209-228.

Hu, L. T., & Bentler, P. M. (1995). Evaluating model fit. In Hoyle, R. H. (Ed.). Structural equation modelling: Concepts, issues and applications (pp. 77-99). Thousand Oaks: Sage.

Iversen, H. (2004). Risk-taking attitudes and risky driving behavior. Transportation Research Part F, 7(3), 135-150.

Jóreskog, K. G., & Sórbom, D. (1993). LISREL 8: Structural equation modelling with the SIMPLIS command language. Chicago: Scientific Software.

Lemaire, J. (1988). A comparative analysis of most European and Japanese Bonus-malus Systems. Journal of Risk and Insurance, 55(4), 660-681.

Lemaire, J. (1995). Bonus-Malus Systems in Automobile Insurance. Boston Kluwer Academic Publisher.

López, C., Fernández, C., & Mariel, P. (2002). Índices de satisfacción del consumidor: Una aplicación de modelos de ecuaciones estructurales a la industria automovilística española. Working paper series Departamento de Econometría y Estadística de la Universidad del País Vasco.

Matthews, G., Dorn, L., & Glendon, A. (1991). Personality correlates of driver stress. Personality and Individual Differences, 12(6), 535-549.

Park, S., Lemaire, J., & Chua, C. T. (2009). Is the design of Bonus-Malus Systems influenced by insurance maturity or national culture? Evidence from Asia. The Geneva Papers, 35, 7-27.

Pitrebois, S., Denuit, M., & Walhin, J. F. (2006). Multi-Event Bonus-Malus Scales. The Journal of Risk and Insurance, 73(3), 517-528.

Richaudeau, D. (1999). Automobile Insurance Contracts and Risk of Accident: An Empirical Test Using French Individual Data. Geneva Papers on Risk and Insurance Theory, 24, 97-114.

Schermelleh-Engel, K., & Moosbrugger, H. (2003). Evaluating the Fit of Structural Equation Models: Tests of Significance and Descriptive Goodness-of-Fit Measures. Methods of Psychological Research Online, 8(2), 23-74.

Schwebel, D. C., Severson, J., Ball, K. K., & Rizzo, M. (2006). Individual difference factors in risky driving: the roles of anger/hostility, conscientiousness, and sensation-seeking. Accident Analysis and Prevention, 38, 801-810.

Segovia-González, M. M., Contreras, I., & Mar-Molinero, C. (2009). A DEA analysis of risk, cost, and revenues in insurance. Journal of Operational Research Society, 60, 1483-1494.

Turner, C., & McClure, R. (2003). Age and gender differences in risk-taking behaviour as an explanation for high incidence of motor vehicle crashes as a driver in young males. Injury Control and Safety Promotion, 10(3), 123-130.

Zuckerman, M., & Kuhlman, M. (2000). Personality and Risk-Taking: Common Bisocial Factors. Journal of Personality, 68(6), 999-1029.