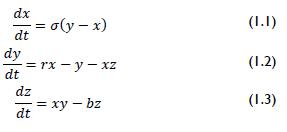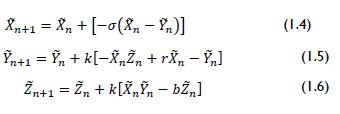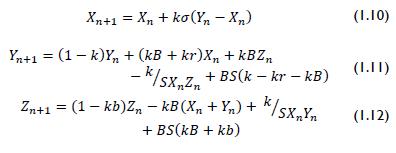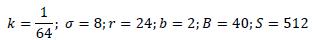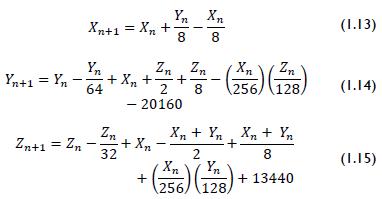Modulating electrocardiographic signals with chaotic algorithms
Modulación de señales electrocardiográficas mediante algoritmos caóticos
DOI:
https://doi.org/10.15446/ing.investig.v32n2.31939Keywords:
algorithm, chaotic signal, ECG signal (en)algoritmos, ecuaciones caóticas, señal de electrocardiograma (es)
Chaos theory is becoming increasingly applied to areas like communications, telemedicine and processing signals and images. Algorithms generating chaotic signals can be used for generating, encrypting and encoding carriers. This work proposes a transmission method allowing electrocardiogram (ECG) signals obtained from a patient to be combined with algorithms generating chaotic signals, based on the Lorenz equation system. Acceptable results were obtained regarding noise and other traditional modulation methods.
Las aplicaciones de la teoría del caos en ramas como las comunicaciones, la telemedicina y el procesamiento de señales e imágenes, son cada vez más frecuentes. Los algoritmos que generan señales caóticas pueden ser utilizados para la generación de portadoras, la encriptación y la codificación, entre otras aplicaciones. En este trabajo se plantea un método de transmisión que permite combinar señales electrocardiográficas (ECG) obtenidas de un paciente, con algoritmos que generan señales caóticas utilizando como base el sistema de ecuaciones de Lorenz. En este proceso se obtienen resultados aceptables frente al ruido y otros métodos de modulaciones tradicionales.
Modulating electrocardiographic signals with chaotic algorithms
Modulación de señales electrocardiográficas mediante algoritmos caóticos
E. Barbara1, E. Alba2, O. Rodríguez3
1 Eduardo Barbará Morales. Affiliation: Instituto Superior Politécnico José. A. Echeverría, Cuba. MSc. in bioengineering, BSc. in Telecommunications and electron-ics, Instituto Superior Politécnico José. A. Echeverría, Cuba. E-mail: eduardobm@electrica.cujae.edu.cu
2 Emiliano Alba Blanco. Affiliation: Instituto Superior Politécnico José. A. Echeverría, Cuba. MSc. in Systems and radio-communications, BSc. in Electric Engineering Instituto Superior Politécnico José. A. Echeverría, Universidad de La Habana, Cuba. E-mail: emiliano@electrica.cujae.edu.cu .
3 Oscar Rodríguez Ramírez. Affiliation: Instituto Superior Politécnico José. A. Echeverría, Cuba. BSc. in Electric Engineering Instituto Superior Politécnico José. A. Echeverría, Universidad de La Habana, Cuba. E-mail: oscar@electrica.cujae.edu.cu
ABSTRACT
Chaos theory is becoming increasingly applied to areas like communications, telemedicine and processing signals and images. Algorithms generating chaotic signals can be used for generating, encrypting and encoding carriers. This work proposes a transmis-sion method allowing electrocardiogram (ECG) signals obtained from a patient to be combined with algorithms generating chaotic signals, based on the Lorenz equation system. Acceptable results were obtained regarding noise and other traditional modulation methods.
Keywords: algorithm, chaotic signal, ECG signal.
RESUMEN
Las aplicaciones de la teoría del caos en ramas como las comunicaciones, la telemedicina y el procesamiento de señales e imágenes, son cada vez más frecuentes. Los algoritmos que generan señales caóticas pueden ser utilizados para la generación de portadoras, la encriptación y la codificación, entre otras aplicaciones. En este trabajo se plantea un método de transmisión que permite combinar señales electrocardiográficas (ECG) obtenidas de un paciente, con algoritmos que generan señales caóticas utilizando como base el sistema de ecuaciones de Lorenz. En este proceso se obtienen resultados aceptables frente al ruido y otros métodos de modulaciones tradicionales.
Palabras clave: algoritmos, ecuaciones caóticas, señal de electrocardiograma.
Received: December 12th 2011 Accepted: June 25th 2012
Introduction
Chaos theory is concerned with the qualitative study of unstable aperiodic behavior in nonlinear, deterministic dynamic systems. Aperiodic behavior is observed when a variable reflects regular repetition of values describing system state.
Non-linearity is fundamental, especially when manifest in chaotic algorithms and equation systems (Barbará, Martinez, 2008).
This paper discusses the concept of chaos as a system of equations resulting from a deterministic process occurring in nonlinear and feedback systems.
This study was aimed at modulating and demodulating electrocardiographic signals using Lorenz model equations. The models used improve randomness without altering the original chaotic state; results are compared against noise and traditional modulation methods.
Model chaotic equations
The model for generating chaotic signals discussed in this research was related to the Lorenz model (Rodríguez, Alvarez, 2010) (González, Larrondo, 2006). Lorenz was interested in hydrodynamic equation solutions' predictability; the system was obtained by equations 1.1, 1.2 and 1.3:
The above system was a continuous system expressed in terms of derivatives of x, y and z, needing to be discretised for further processing an electrocardiographic signal. This was performed by first order Euler equations yielding a system as shown in 1.4, 1.5 and 1.6 (Blanchet, 2006), (Murali, 1993).
where k was a scalar parameter of time. The system was ex-pressed in discrete form (i.e. a 3D map). The following transfor-mations were applied to reduce complexity and elevation scale shown in equations 1.7, 1.8 and 1.9:
where B and S were elevation and scaling parameters, respectively. Equations 1.10, 1.11 and 1.12 show the results:
This study has adopted the following system simulation values:
Applying these values to equations 1.10, 1.11, 1.12 resulted in 1.13, 1.14, and 1.15:
The system of equations 1.13, 1.14 and 1.15 is known as 3D mapping where the modulating key comprises the variable's least significant Xn 8 bit (González and Larrondo, 2006; Sobhy and Sheata, 1997).
Transformations and elevation and arithmetic scales with natural numbers were used to simplify the computational implementation of this system of equations.
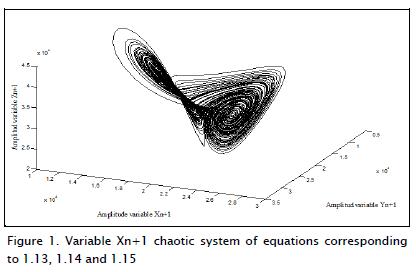
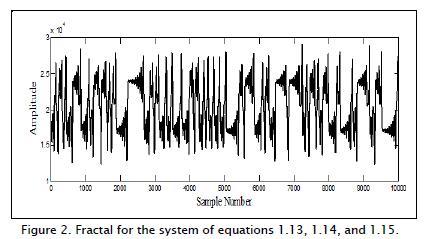
This map was structurally stable. Graphical analysis of equation 1.12, 1.13 and 1.14 system may be checked to ensure that it actually reaches chaos. This was simulated in Matlab mathemati-cal assistant (V-7.10.0); initial condition values used were Xn=19400, Yn=21315, and Zn=32032. These values were selected as they belonged to the phase space in which the algorithm had chaotic behaviour (Figures 1 and 2).
The design and simulation of a electrocardiographic signal (ECG) modular system obtained from a real patient using chaotic variables Xn+1 and Zn+1 as carriers is described. These signals were generated using the system of equations 1.12, 1.13 and 1.14 shown above.
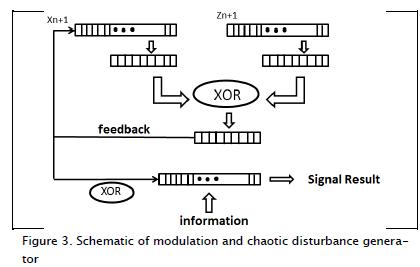
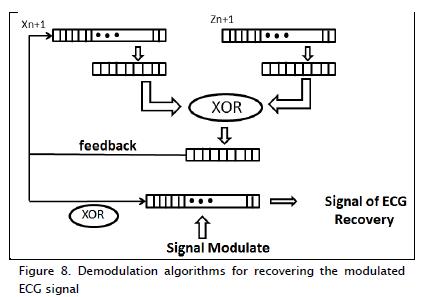
The block diagram in Figure 3 describes modulation by the algorithm for the disruption of a chaotic signal.
Variables Xn+1 and Zn+1 in this algorithm were taken with an initial 16 bit length; each 8 bit was taken from the bottom by a logical AND operation. An XOR followed and was stored in an 8 bit register. Such bits were then fed back again to the position where they were taken in variable Xn+1 to form a new 16 bit word (Figure 3). This feedback was an excitation to the system of equations forming the basis for the disturbance performed in each iteration of this algorithm. The chaotic signal had new behaviour from this moment on and it could be said that the Lo-renz system had then been disturbed (González, Larrondo, 2006).
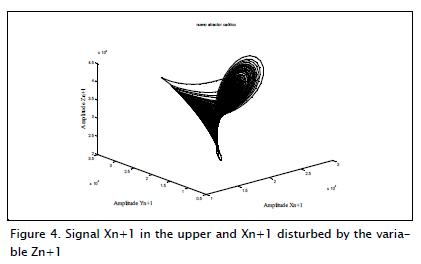
Figure 4 shows the chaotic behaviour of variable originally Xn+1 and then after being disturbed.
The variables' pattern differed as time elapsed; the correlation coefficients matrix obtained with Matlab for the Xn+1 and Xn+1 signal disturbed below shows that both signals had very low correlation (Yu, 2001; Murali, Lakshmanan, 1993).
Although new signal Xn+1 pattern became modified, this continued to be chaotic and retained these systems' properties (González, 2006; Lawrence, 2000).
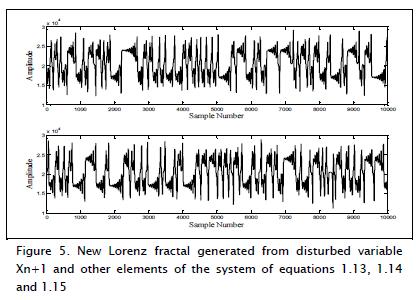
Figure 5 shows the Lorenz fractal generated from new modified signal Xn+1.
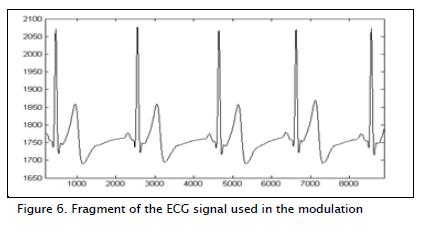
Modulation occurred when performing XOR between modified chaotic variable Xn+1 as described above. The ECG signal to be conveyed provided useful data or information in this case (Figure 6).
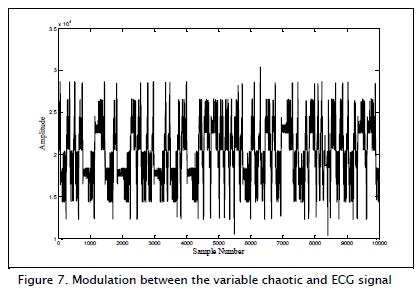
Figure 7 shows applied modulation between chaotic and ECG signal.
Demodulation algorithm
The demodulation algorithm was similar to that shown in Figure 3, but in this case, the useful signal for ECG had to perform the XOR logic operation. The chaotic variable disturbed by the modulated signal was received, again obtaining a useful signal. It is worth noting that a chaotic system of equations used to transmit in the modulator must be generated exactly in the unit; this must be perfectly synchronised with the initial conditions mentioned above. Figure 8 shows the block diagram for this process.
Results and Discussion
This model's behaviour was analysed against noise and compared to traditional modulation method.
The simulations were performed in Matlab (Blanchet and Char-bit, 2006) and the noise chosen for this process was additive white Gaussian noise (AWGN) as this is a mathematical model of noise resembling overall communications' channel features.
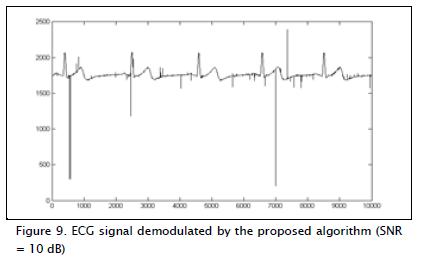
Recovery was simulated ECG signal for various signal to noise ratio (SNR) values. The signal to be modulated was contaminated with AWGN in a first case, maintaining SNR = 10 dB. The ECG signal recovered with the detection scheme shown in Figure 8 is illustrated in Figure 9.
Values were calculated from the matrix of coefficient correlation between original signal used in modulation and that recovered in the above conditions, resulting in:
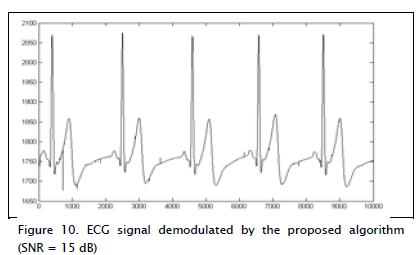
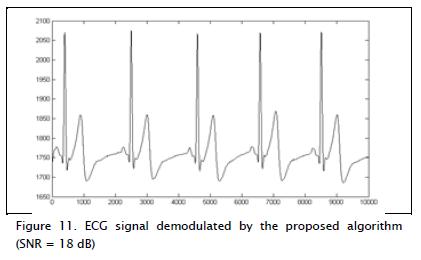
Recovery was also simulated for 15 dB and 18 dB SNR values (Figures 10 and 11, respectively.
The matrix of correlation coefficients with the original signal for the demodulated signal having SNR = 18dB resulted in:
1.0000 1.0000
1.0000 1.0000
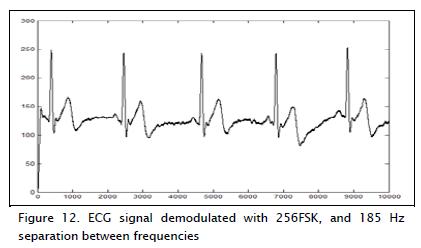
Comparisons were also made with traditional modulation meth-ods, such as frequency shift keying (FSK) digital modulation frequency. The ECG signal was modulated in this case by using 256 levels so that a symbol consisted of 8 bits. Initial separation between carrier frequencies was 185 Hz. This signal was contaminated with AWGN noise (SNR = 18 dB). A non-coherent FSK receiver was used for demodulation (Sklar, 2002), which is easy to implement and does not require synchronisation. The result was obtained by demodulating the signal (as shown in Figure 12).
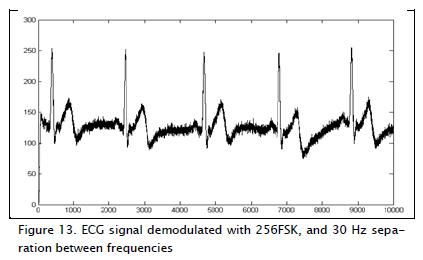
The modulation described above involved a parameter regarding separation between desired modular frequency tones; this parameter had an impact on signal demodulation. As it became smaller, separation between tones became reduced so that it became more difficult to identify amongst tones close proximity, and worsened detection. When frequency tones were spaced at 30 Hz, maintaining SNR = 18 dB, then it could be seen that the recovered ECG signal had noise levels (Figure 13).
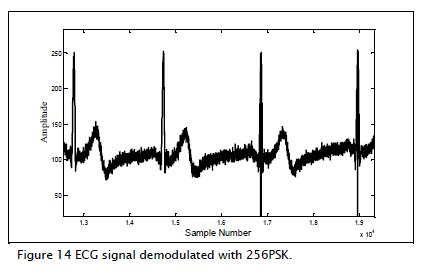
Another modulation method proposed for comparison was phase shift keying (PSK) linear phase digital modulation using 256 levels.
Then the resulting modulation was contaminated by additive white Gaussian noise (18 dB SNR).
The ECG signal recovered for this SNR value had the shape shown in Figure 14. The effects of noise can be seen, introducing distortion into the retrieved information. Correlation coefficient matrix values with the original signal resulted in:
1.0000 0.9566
0.9566 1.0000
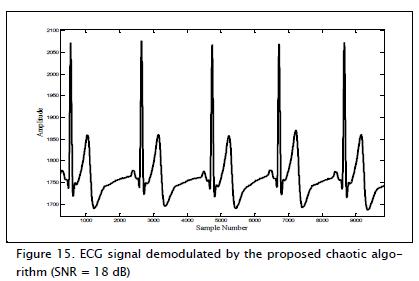
The SNR signal was recovered with better fidelity in the proposed algorithm for the chaotic system Lorenz equations, taking into account the above conditions (Figure 15). The resulting correlation coefficient matrix was:
1.0000 1.0000
1.0000 1.0000
Better results were obtained for the proposed chaotic modula-tion algorithm for the same SNR value.
Conclusions
This work has shown an algorithm allowing ECG signal modulation using a chaotic carrier signal. Simulations were also performed for the recovery of an ECG signal modulated with different SNR values. Acceptable results were obtained; this modulation method had acceptable characteristics against noise and also provided advantages over traditional modulation methods.
References
Barbará E., and Martínez M., "Generación discreta de señales caóticas". Telecommunications and Electronic Engineering thesis, La Habana, Cuba, 2008.
González M, Larrondo, H, Gayoso C. Digital Dignal Transmission with chaotic encryption design and evaluation on FPGAS, 2006.
Blanchet G. Charbit M. "Digital signal and image processing using MATLAB" ISTE Ltd, 2006.
Murali K., Lakshmanan M., "Transmission of signals by synchronization in a chaotic Vander Pol-Duffing oscillator", Phys. Rev. E, vol. 48, no. 3, pp R1624-R1626, 1993.
Lorenzo, M. Influencia del ruido Gaussiano correlacionado en la sincronización de los sistemas caóticos. PhD Physics thesis, Santiago de Compostela, Chile, 2000.
Rodriguez J, E. D., and Álvarez, E., "Sistema de Comunicación Digital mediante modulación caótica por posición de pulsos". BSc Telecommunications and Electronic Engineering thesis, La Habana, Cuba, 2010.
Sobhy, M, Aseeri, M. Shehata, E. R., "Real time implementation of continuous (Chua and Lorenz) chaotic generator models using digital hardware". University of Kent, UK, 1997.
References
Barbará E., and Martínez M., “Generación discreta de señales caóticas”. Telecommunications and Electronic Engineering thesis, La Habana, Cuba, 2008.
González M, Larrondo, H, Gayoso C. Digital Signal Transmission with chaotic encryption design and evaluation on FPGAS, 2006.
Blanchet G. Charbit M. “Digital signal and image processing using MATLAB” ISTE Ltd, 2006. DOI: https://doi.org/10.1002/9780470612385
Murali K., Lakshmanan M., “Transmission of signals by synchronization in a chaotic Vander Pol-Duffing oscillator”, Phys. Rev. E, vol. 48, no. 3, pp R1624-R1626, 1993. DOI: https://doi.org/10.1103/PhysRevE.48.R1624
Lorenzo, M. Influencia del ruido Gaussiano correlacionado en la sincronización de los sistemas caóticos. PhD Physics thesis, Santiago de Compostela, Chile, 2000.
Rodríguez J, E. D., and Álvarez, E., “Sistema de Comunicación Digital mediante modulación caótica por posición de pulsos”. BSc Telecommunications and Electronic Engineering thesis, La Habana, Cuba, 2010.
Sobhy, M, Aseeri, M. Shehata, E. R., “Real time implementation of continuous (Chua and Lorenz) chaotic generator models using digital hardware”. University of Kent, UK, 1997.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Maricela Jiménez Rodríguez, Carlos Eduardo Padilla Leyferman, Juan Carlos Estrada Gutiérrez, María Guadalupe González Novoa, Horacio Gómez Rodríguez, Octavio Flores Siordia. (2018). Steganography applied in the origin claim of pictures captured by drones based on chaos. Ingeniería e Investigación, 38(2), p.61. https://doi.org/10.15446/ing.investig.v38n2.64509.
Dimensions
PlumX
Article abstract page views
Downloads
License
Copyright (c) 2012 Eduardo Barbará Morales, Emiliano Alba Blanco, Oscar Rodríguez Ramírez

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors or holders of the copyright for each article hereby confer exclusive, limited and free authorization on the Universidad Nacional de Colombia's journal Ingeniería e Investigación concerning the aforementioned article which, once it has been evaluated and approved, will be submitted for publication, in line with the following items:
1. The version which has been corrected according to the evaluators' suggestions will be remitted and it will be made clear whether the aforementioned article is an unedited document regarding which the rights to be authorized are held and total responsibility will be assumed by the authors for the content of the work being submitted to Ingeniería e Investigación, the Universidad Nacional de Colombia and third-parties;
2. The authorization conferred on the journal will come into force from the date on which it is included in the respective volume and issue of Ingeniería e Investigación in the Open Journal Systems and on the journal's main page (https://revistas.unal.edu.co/index.php/ingeinv), as well as in different databases and indices in which the publication is indexed;
3. The authors authorize the Universidad Nacional de Colombia's journal Ingeniería e Investigación to publish the document in whatever required format (printed, digital, electronic or whatsoever known or yet to be discovered form) and authorize Ingeniería e Investigación to include the work in any indices and/or search engines deemed necessary for promoting its diffusion;
4. The authors accept that such authorization is given free of charge and they, therefore, waive any right to receive remuneration from the publication, distribution, public communication and any use whatsoever referred to in the terms of this authorization.